9.2.Колебания системы с одной степенью свободы

Механическая система с одной степенью свободы в случае голономных, идеальных, неосвобождающих связей имеет одну обобщенную координату q и ее движение описывается одним уравнением Лагранжа:

. (9.1)

Обобщенную силу Q можно считать состоящей из трех частей:

Q=QП+QФ+QВ. (9.2)

Обобщенная сила потенциальных сил выражается через потенциальную энергию по формуле Q^П=–П/q.

Q^Ф – обобщенная сила от действия сил сопротивления.

Часть обобщенной силы Q^В получается от так называемых возмущающих сил, зависящих прежде всего от времени.

Рассмотрим малые колебания системы с одной степенью свободы под действием одних потенциальных сил. Считаем, что сил сопротивления и возмущающих сил нет. Такие колебания называются собственными, или свободными. В случае малых колебаний системы получается линейное дифференциальное уравнение для обобщенной координаты q.

Выражение для кинетической энергии можно представить в виде

,

где a – называется коэффициентом инерции. Потенциальная энергия определяется в соответствии с выражением П(q)=1/2cq², где c – коэффициент жесткости. Составляющие уравнения Лагранжа для этого случая имеют вид:

.

Подставляя эти значения производных в уравнение Лагранжа, получим дифференциальное уравнение малых, собственных колебаний системы с одной степенью свободы:

. (9.3)

Если разделить обе части уравнения (9.3) на a и обозначить c/a=k², то получим дифференциальное уравнение собственных колебаний системы с одной степенью свободы в форме:

. (9.4)

Постоянная величина k называется круговой, или циклической частотой колебаний. Для прямолинейных колебаний материальной точки (рис. 9.2), на которую действует сила F_x=–c₀x, имеем , где k²=c₀ /m.

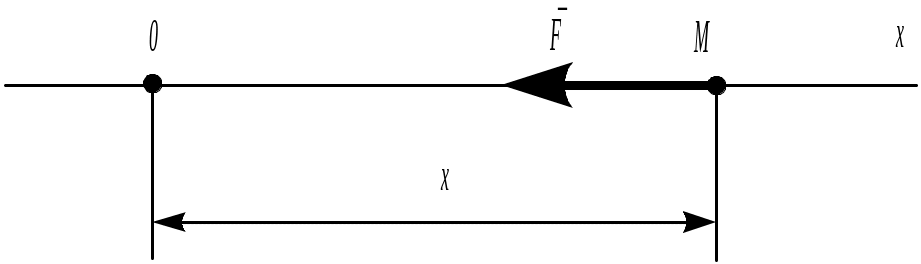
Рис. 9.41

Решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами (9.4) будем искать в виде q=e^t. После подстановки этого выражения в (9.4) получаем характеристическое уравнение: ²+k²=0.

Это квадратное уравнение имеет два чисто мнимых корня _1,2=ki. Решение уравнения (9.4) можно представить в виде

q=C₁cos(kt)+C₂sin(kt) (9.5)

и для обобщенной скорости

. (9.6)

Произвольные постоянные C₁ и C₂ определяются из начальных условий: , где q₀ и – начальные значения обобщенной координаты и обобщенной скорости. Используя выражения для q и при t=0, получаем . Подставляя их значения в (9.5), имеем:

(9.7)

9.3.Общие положения теории удара

Силы, действующие на тела, подразделяют на силы, изменяющие скорости точек в течение некоторого конечного промежутка времени (конечные силы) и силы, изменяющие скорости точек в течение весьма малого промежутка времени (мгновенные, или ударные, 0.1–0.01 с).

Мгновенной, или ударной, называют силу, действующую в течение весьма малого промежутка времени, но достигающую при этом таких больших значений, что ее импульс за это время становится конечной величиной.

Пусть F – ударная сила,  – время действия этой силы, тогда импульс за промежуток времени : . Здесь S – конечная величина. Это возможно в случае, если величина силы порядка 1/, где  – малая величина. Импульс S называют ударным. Явление, при котором возникают мгновенные, или ударные, силы, называют ударом.

Процесс удара рассмотрим на примере соударения двух тел А и В (рис. 9.3). Допустим, что соприкосновение происходит в одной точке.

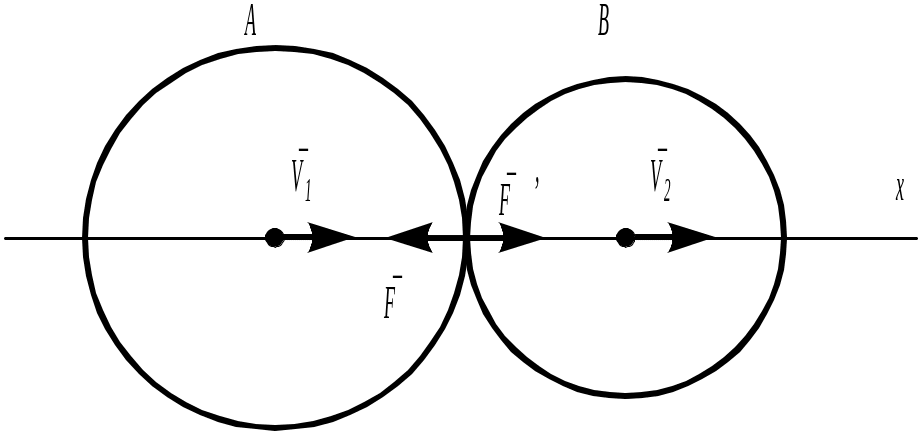
Рис. 9.42

Тело А в момент соприкосновения имеет скорость V₁, а тело В – скорость V₂ (для определенности допустим, что V₁> V₂). Общую нормаль к поверхности соударяющихся тел в точке их соприкосновения назовем линией удара.

Удар называют центральным, если центры масс соударяющихся тел лежат на линии удара. Центральный удар называют прямым, если скорости центров масс соударяющихся тел в начале удара направлены по линии удара. Тела А и В считаем абсолютно гладкими. После момента соприкосновения оба тела деформируются, при этом скорость тела А уменьшается, а скорость тела В увеличивается. Процесс деформации заканчивается тогда, когда скорости тел станут равными. Эту часть явления удара называют фазой деформации ₁. Ударный импульс силы F за фазу деформации: .

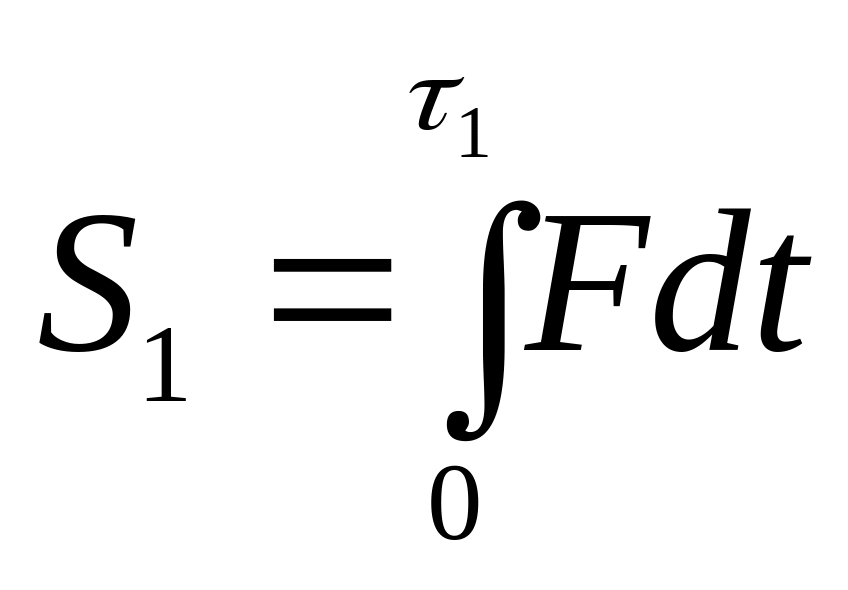Импульс силы за эту же фазу обозначим . Если тела упруги, то после деформации они восстанавливают свою форму целиком и полностью. Эту часть явления удара называют фазой восстановления (продолжительность этой фазы ₂). Импульс ударной силы, действующей на тело А, за эту фазу восстановления

,

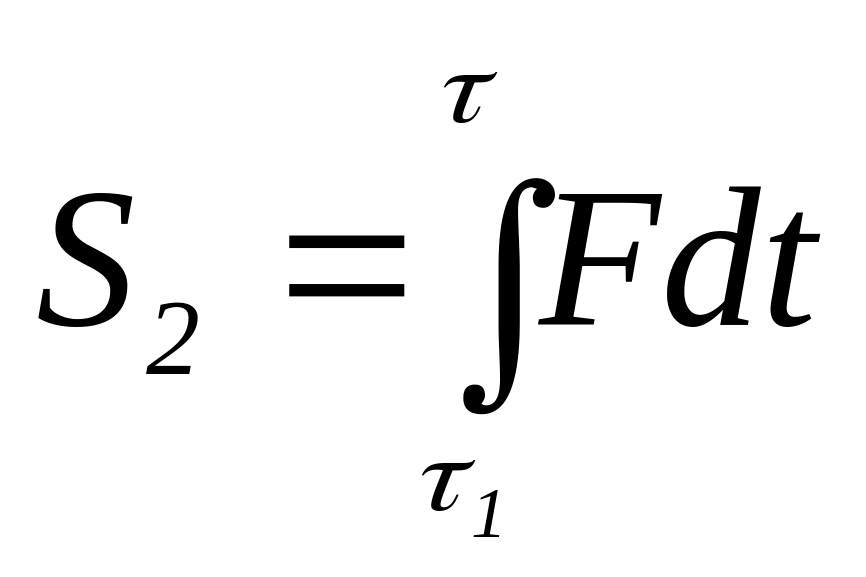где =₁+₂ (полная продолжительность удара).

Эффект действия ударной силы оценивается по ее импульсу – конечной величине. Общие теоремы, применяемые к удару, формулируют так, чтобы в них входили не ударные силы, а ударные импульсы.

Упругость соударяющихся тел оценивают по коэффициенту восстановления k=S₂/S₁.

При k=0 величина S₂=0, т.е. фаза восстановления отсутствует – абсолютно неупругий удар.

В случае k=1 величина S₂=S₁ можно считать, что за фазу восстановления тела полностью восстанавливают свою форму (абсолютно упругий удар).

При 0<k<1 происходит удар тел средней упругости и этот удар называют упругим.

Основное уравнение динамики точки при ударе: изменение количества движения материальной точки за время удара равно ударному импульсу, приложенному к точке

mu – mv=S,

где скорость точки в начале удара v, в конце удара u.

Из этого уравнения для скорости материальной точки в конце удара находим

u=v+S/m .

На рис. 9.4 указаны скорость v в начале удара, ударный импульс S и скорость u в конце удара, при этом векторы v и u построены в одной точке.

Рис. 9.43