итоговый отчет

поверхностным натяжением и кинетическими эффектами на фронте кристаллизации,

аналитически получил стационарное решение уравнения теплопроводности в двух и трехмерном случае в форме семейства софокусных парабол и параболоидов вращения соответственно, причем их вершины растут с постоянной скоростью υt и радиусом кривизны Rt при заданном переохлаждении расплава [126]. Однако эти решения определяют непрерывное семейство значений υt и Rt , удовлетворяющее условию

υt × Rt =const. Введение в задачу поверхностного натяжения в рамках так называемой теории разрешимости [127, 128] приводит к диффузионному уравнению типа уравнения Шредингера с дискретным семейством решений. Таким образом, особенностью проблемы свободной границы является множественность решений. В то же время эксперимент показывает, что в диффузионно-контролируемых условиях при заданном переохлаждении расплава реализуется только одно решение. Поэтому проблема свободной границы связана с проблемой отбора структуры [129-137]. Дискуссия по критериям отбора

(принцип максимума производства энтропии, маргинальной устойчивости и др.) до сих пор носит гипотетический характер.

Дальнейшее развитие теории неравновесного роста связано с анализом устойчивости отобранного решения для объяснения роста разветвленных древовидных

(дендритных) структур. Происхождение боковых ветвей дендрита, в принципе, можно отнести к диффузионной неустойчивости Маллинза - Секерки. Маллинз и Секерка показали, что плоский фронт кристаллизации, растущий в переохлажденном расплаве,

морфологически неустойчив по отношению к бесконечно малым возмущениям с определенной длиной волны, определяемой поверхностным натяжением фазовой границы, тепловыми свойствами расплава и скрытой теплотой кристаллизации [138].

Триггерами ветвления могут быть тепловой шум, расщепление вершины дендрита или осцилляции ее скорости роста [123]. В последнем случае показано, что нелинейные аспекты уравнения движения фазовой границы могут привести к устойчивой колебательной моде роста, которая действует как источник ветвления. В [127, 139-143] на основе анализа зависящего от времени поведения боковых ветвей и показано, что кроме скорости и кривизны вершины дендрита эволюция последнего характеризуется двумя основными скейлинговыми параметрами: положением первой боковой ветви, отсчитанной от вершины дендрита и выраженной в единицах Rt , а также фрактальной размерностью контура проекции всего дендрита d f .

42

ветвями и т.д. по заданному переохлаждению расплава. Большинство теоретических исследований дендритного роста предполагают устойчивый рост в изначально чистом переохлажденном расплаве [148-151]. Для чистых веществ фундаментальным механизмом, контролирующим затвердевание, является теплопроводность. Скрытая теплота, которая выделяется при затвердевании материала вблизи фронта кристаллизации,

должна быть отведена для того, чтобы дальнейшее затвердевание было бы возможно.

Безразмерное тепловое диффузионное поле вблизи дендрита обычно выбирается в

единицы измерения переохлаждения. Это тепловое поле u удовлетворяет диффузионному уравнению

В случае раствора рост кристалла лимитируется диффузией примеси, а не диффузией тепла [152-159]; тепловой диффузией (т.е. теплопроводностью) в первом приближении можно пренебречь, так как она значительно быстрее диффузии примеси. В

результате концентрация примеси определяется диффузионным полем, которое играет такую же роль как тепловое поле с заменой D на коэффициент диффузии примеси в растворе. Это приводит к математическому описанию проблемы, которое оказывается почти полностью идентичным случаю роста кристалла из переохлажденного расплава.

Поэтому мы ограничимся рассмотрением теории дендритного роста из чистого

переохлажденного расплава. Вдали от дендрита диффузионное поле u∞ = 0 в

соответствии с уравнением (2.6). Вблизи фронта затвердевания граничные условия задаются законом сохранения энергии и локальной температурой. Из закона сохранения следует, что

45

Tm – равновесная температура плавления на плоском фронте кристаллизации. Второй терм в правой части уравнения (2.9) есть коррекция Гиббса-Томсона для температуры плавления на искривленной поверхности, k – ее локальная кривизна и

есть капиллярная длина, пропорциональная поверхностной свободной энергии межфазной

границы твердое тело-жидкость γsl , которая в общем случае зависит от угла θ между

нормалью к фазовой границе и направлением преимущественного роста. Третий терм в правой части уравнения (2.9) представляет собой кинетическую коррекцию υn / β (где β

– кинетический коэффициент роста), которая описывает отклонение от локального термодинамического равновесия на движущейся фазовой границе. Кинетические эффекты и анизотропии поверхностных свойств играют очень важную роль в современных теориях дендритного роста.

Диффузионное уравнение вместе с граничными условиями на движущейся фазовой границе составляет так называемую модифицированную проблему Стефана. Она приводит к сложному нелинейному, нелокальному интегро-дифференциальному уравнению, которое не может быть решено непосредственно без последующих приближений. Обычно для упрощения проблемы пренебрегают кинетическими эффектами. В симметричной модели [123] тепловые свойства твердой и жидкой фаз предполагаются одинаковыми. В этом случае уравнение движения может быть записано в

виде

46

где ξ(r, t) обозначает мгновенную позицию фронта затвердевания в момент времени t , а

Здесь обозначает двумерный градиент. Симметричная модель является исходной моделью многих теоретических исследований дендритного роста.

Решение Иванцова. То обстоятельство, что форма дендрита может быть аппроксимирована параболоидом вращения, было предположено впервые Папапетроу

(Papapetrou [160]) в 1935 г. Первый аналитический подход к проблеме теплового потока в ходе установившегося роста был предложен Иванцовым в 1947г. [126]. Иванцов пренебрег эффектом Гиббса-Томсона и кинетическим эффектом и показал, что диффузионное поле около дендрита может быть рассчитано в цилиндрически симметричных параболических координатах. Решение Иванцова это дендрит с сохраняющейся во времени формой, который растет с постоянной скоростью вершины υt .

В этом приближении поверхность дендрита имеет форму параболоида вращения и дается изотермой

Физический смысл решения Иванцова в течение многих лет оставался неясным. С другой стороны, в ранних экспериментах было обнаружено, что вершины реальных дендритов,

особенно образующихся в материалах с относительно низкой анизотропией, например, в

большинстве металлов и некоторых органических материалах, действительно более или менее похожи на параболоиды вращения. Однако решение Иванцова дает информацию только о произведении υt × Rt в соответствии с уравнением (2.16). Это означает, что оно определяет непрерывное семейство решений υt и Rt , в то время как эксперимент

47

показывает единственное значение скорости роста υt и радиуса Rt вершины дендрита при заданном переохлаждении [145]. Наконец, решение Иванцова оказывается неустойчивым по отношению к образованию боковых ветвей [150].

Гипотеза маргинальной устойчивости. Введение поверхностного натяжения в качестве дополнительного терма в уравнение (2.14) приводит к появлению максимума на зависимости υt (Rt ) . Эта максимальная скорость может соответствовать динамически отобранному состоянию системы. Но предложенная Д.Е. Темкиным [133] гипотеза максимальной скорости была опровергнута экспериментами с сукцинонитрилом,

проведенными Гликсманом и др. (см. в [145]) Более успешная попытка описания реального состояния дендрита была предпринята в рамках гипотезы маргинальной устойчивости [132]. Лангер и Мюллер-Крюмбхар проанализировали стабильность параболических дендритов, используя поверхностное натяжение как возмущение, и

обнаружили, что непрерывные решения Иванцова разделяются на стабильную и нестабильную области [161, 162]. Они предположили, что динамическое состояние,

отобранное физической системой, соответствует точке маргинальной устойчивости,

разделяющей стабильную и нестабильную области. Эта гипотеза приводит к

дополнительному соотношению между υt и Rt :

где σ* называют константой стабильности. В моделях обычно предполагается, что σ не зависит от переохлаждения. Экспериментально обнаружено, однако, что значение σ

варьируется от вещества к веществу и зависит от переохлаждения для некоторых веществ

[148, 163]. Вместе с тем, Rt не является вполне определенной величиной. Поэтому дискуссия по поводу того, является ли величина υt Rt 2 константой, обсуждается в [148] на основе анализа более тщательно измеренных значений Rt .

Теория разрешимости. Дальнейшее развитие теории отбора дендритной структуры начинается с так называемой микроскопической теории разрешимости [164].

Главная особенность этой теории состоит в том, что поверхностное натяжение играет роль сингулярного возмущения, которое накладывает условие разрешимости на стационарные состояния. В отличие от решений Иванцова существует только дискретный ряд решений и только одно из этих решений оказывается динамически устойчивым [123,

48

164]. Наиболее существенный и удивительный результат состоит в том, что не существует стабильных решений в случае изотропной поверхностной энергии и что для существования решения необходима анизотропия свободной энергии поверхности.

Интересно отметить, что константа стабильности σ снова оказывается стабильным параметром [149]. Однако, лежащая в основе теории система уравнений является лишь приближением. Эффекты, связанные с микроскопической структурой кристалла и кинетикой роста здесь игнорируются, кроме того, действия шума и образование боковых ветвей также не учтены, в то же время они могут играть очень важную роль при небольших степенях переохлаждения. Кроме того, эксперименты не подтверждают предсказание зависимости константы стабильности от степени анизотропии:

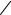[165-170]. Это может быть связано с трудностью получения экспериментальных значений анизотропии, достаточно точных для тестирования этой теории. Таким образом, микроскопическая теория разрешимости не может в настоящее время рассматриваться как подтвержденная экспериментально во всех своих аспектах.

Основной результат двумерной теории разрешимости состоит в том, что для получения стабильного роста необходима также анизотропия поверхностного натяжения.

Анизотропия поверхностного натяжения вводится с помощью капиллярной длины,

которая зависит от угла θ между нормалью к фазовой границе в точке и осью ствола дендрита. В случае симметрии четвертого порядка капиллярная длина дается формулой

трехмерный случай не возможна, так как анизотропия поверхностного натяжения вызывает рост дендритов, не обладающих осевой симметрией. Этот факт значительно усложняет теорию трехмерных дендритов.

Первая аналитическая теория трехмерных дендритов, не обладающих осевой симметрией, была развита Бен Амаром и Бренером [171]. Условие разрешимости для этой проблемы обеспечивается отбором и скорости роста и формы фазовой границы.

Отобранная форма для дендрита с кубической анизотропией может быть записана в

49

где все длины даны в единицах радиуса кончика Rt . Важный аспект уравнения (2.19)

заключается в том, что коррекционные слагаемые rm cos(mφ) растут быстрее, чем решение Иванцова. Поэтому это приближение действительно только около вершины, а

вдали от нее появляются сильные отклонения от параболы Иванцова для сколь угодно малой анизотропии. В теории Бен Амара и Бренера первый ненулевой терм коррекции формы найден в пределе малой анизотропии

Эта формула представляет коррекцию формы дендрита с кубической симметрией. Она не зависит от степени анизотропии и может быть использована для аппроксимации контура

кончика дендрита очень близко к вершине (до 2Rt от вершины).

В [172] Бренер получил аналитическое решение проблемы трехмерного дендритного роста. Его решение включает в себя теорию отбора для трехмерного случая,

а также устройство хвостовой части. В случае кристаллических веществ c симметрией четвертого порядка он обнаружил, что возникает четыре «плавника», которые растут на боковой поверхности дендрита. Вблизи вершины дендрита форма может быть описана уравнением (2.19), но вдали от вершины форма описывается в декартовых координатах

(x, y, z) :

для контура плавников, где безразмерный коэффициент a порядка единицы [148]. В [148, 173] этот результат используется для сравнения с данными экспериментального исследования формы вершины дендритов ксенона. Обнаружено, что эта форма почти не зависит от материала и параметры роста близки к уравнению (2.20) в области вершины, а

50