Простейшие колебательные системы
1. Груз на пружине.
Р
ассмотрим
систему, состоящую из бруска массой m
и пружины жесткостью k.
Пусть брусок лежит на гладком горизонтальном
столе и связан горизонтальной пружиной
с вертикальной стенкой. При отклонении
бруска от положения равновесия на
величину x
вдоль направления пружины возникает
сила упругости
.
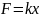Эта сила направлена в сторону положения
равновесия, то есть является возвращающей
силой и пропорциональна величине
отклонения. Причем коэффициентом
квазиупругой силы является жесткость
пружины k.
Значит период гармонических колебаний
груза на пружине равен:
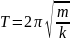
2. Математический маятник.
М
атематическим
маятником называется маленький тяжелый
шарик (материальная точка), подвешенный
на длинной тонкой невесомой нити.
Отклоним шарик от положения равновесия
на угол
и отпустим. Равнодействующая сил тяжести
и натяжения нити будет равна
и направлена по касательной к траектории
в сторону положения равновесия. Если
линейное отклонение шарика от положения
равновесия (длина дуги) равно х, то
,
где l
– длина нити. Тогда
.
Получается, что при отклонении шарика
возникает возвращающая сила, но она не
пропорциональна величине отклонения
х. То есть произвольные колебания
математического маятника не являются
гармоническими. Однако для малых углов
выполняется приближение
.
Тогда для возвращающей силы можно
написать:
.
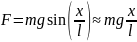Возвращающая сила при этом становится
пропорциональна отклонению от положения
равновесия, а коэффициент квазиупругой
силы равен
.
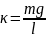Значит малые колебания математического
маятника являются гармоническими.
Период малых колебаний математического
маятника равен:
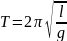
Малыми называются колебания, при которых максимальные отклонения от положения очень малы. Для математического маятника колебания, при которых угол отклонения не превышает 10 - 15, с достаточной точностью можно считать малыми, то есть гармоническими.
Гармонические колебания являются наиболее простым, но очень распространенным типом колебаний. Для большинства реальных колебательных систем малые свободные колебания являются гармоническими.
Энергия при гармонических колебаниях
Рассмотрим простейшие гармонические колебания – колебания груза на пружине. Пусть на гладком горизонтальном столе лежит груз массой m, связанный пружиной жесткостью k с вертикальной стеной. Если вывести груз из положения равновесия, растянув пружину, и отпустить, то возникнут колебания. Если трения и других потерь энергии нет, то эти колебания будут незатухающими и гармоническими. При этом когда тело проходит положение равновесия его скорость, а значит и кинетическая энергия максимальны. А вот деформация пружины, а значит и ее потенциальная энергия в положении равновесия равны нулю. Наоборот при прохождении телом положения максимального отклонения скорость тела, а значит и его кинетическая энергия равны нулю, а деформация пружины и ее потенциальная энергия максимальны.
Так происходит при любых гармонических колебаниях. При прохождении системой положения равновесия кинетическая энергия системы максимальна, а потенциальная равна нулю. При прохождении положения максимального отклонения кинетическая энергия системы равна нулю, а потенциальная максимальна. Во всех промежуточных положениях есть и кинетическая и потенциальная энергии. Однако полная механическая энергия (сумма кинетической и потенциальной) для гармонических колебаний постоянна и равна максимальной кинетической или максимальной потенциальной энергии. Закон сохранения энергии для гармонических колебаний:
Если
система совершает гармонические
колебания, то ее кинетическая и
потенциальная энергии по отдельности
тоже изменяются по гармоническому
закону, но с частотой вдвое большей, чем
частота колебаний координаты, скорости
и ускорения. Так если
,
а
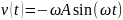то
Аналогично:
