4. Контрольные вопросы

1. Записать различные формы интеграла Дюамеля.

2. Привести выражение, связывающее импульсную и переходную характеристики линейной стационарной цепи.

3. При каких условиях прямоугольный импульс можно использовать для получения импульсной и переходной характеристик цепи?

4. Найти и изобразить графически свертку сигнала, представляющего собой прямоугольный импульс длительностью T и уровнем U₀, с самим собой.

5. На вход цепи подается прямоугольный импульс длительностью T и высотой U₀. Найти и изобразить сигнал на выходе цепи, если ее импульсная характеристика равна

6. На вход цепи подается прямоугольный импульс длительностью T с уровнем U₀. Найти и изобразить сигнал на выходе цепи, если ее переходная характеристика равна

Лабораторная работа № 2 спектральные методы исследования линейных цепей

Цель работы: Изучение понятия частотных характеристик линейных цепей, методов их измерения и способов применения для расчета отклика цепи на заданное входное воздействие.

1. Теоретические сведения

Спектральные (частотные) методы анализа линейных стационарных цепей основаны на применении аппарата рядов и преобразований Фурье, а также на свойствах линейных операторов, описывающих цепи.

1.1. Спектральное представление сигналов

Наряду с динамическим представлением сигналов в виде интегралов наложения в радиотехнике очень широко применяется их спектральное представление, то есть выражение через гармонические сигналы вида

.

Рассмотрим сначала спектральное представление периодических сигналов. Известно, что любой периодический сигнал x(t) с периодом T вида

(1)

может быть представлен в виде ряда Фурье.

,

(2)

где  = 2f₀ = 2/T – циклическая основная частота сигнала, а коэффициенты ряда (2) определяются выражениями:

.

Если коэффициенты разложения a_k и b_k записать в виде

,

так что

,

можно записать другую эквивалентную форму ряда Фурье:

.

(3)

В радиотехнике чаще всего используют комплексную форму ряда Фурье, которую легко получить из выражения (3), применив формулу Эйлера:

.

(4)

Введенные здесь комплексные коэффициенты C_k (k = 0, 1, …) определяются выражениями:

.

(5)

Набор коэффициентов C_k называют спектром периодического сигнала; причем множество модулей |C_k| = A_k/2 составляют амплитудный, а множество аргументов _k = – _k = arg{C_k} – фазовый спектр. Очевидно, для действительных сигналов C_–k = C_k^*. Коэффициент C₀ называется постоянной составляющей сигнала и, в соответствии с формулой (5), определяется как площадь сигнала на периоде, деленная на период. Величины |C_k| имеют смысл амплитуд гармонических составляющих сигнала (гармоник) с частотами k, а набор _k описывает фазовые сдвиги каждой из гармоник. Амплитудный и фазовый спектры изображаются в виде гистограмм, поэтому спектры периодических сигналов часто называют линейчатыми.

В качестве примера вычислим набор коэффициентов C_k прямоугольного периодического сигнала, вид которого показан на рис. 1. Пользуясь выражением (5), получим:

.

Рис. 1. Прямоугольный периодический сигнал и его амплитудный и фазовый спектры

С использованием функции sinc(x) = sin(x)/x, результат может быть записан в другом виде

.

Справа на рис. 1 показаны амплитудный и фазовый спектры прямоугольного периодического сигнала.

Перейдем к спектральному представлению непериодических сигналов. Рассмотрим одиночный импульс конечной длительности x(t) и построим на его основе периодическую импульсную последовательность x_T(t) с периодом T. Разложим построенный периодический сигнал в ряд Фурье (4) и вернемся к исходному импульсу x(t), устремив период к бесконечности. При этом частоты соседних гармоник (k – 1) и k окажутся сколь угодно близкими, то есть дискретный набор частот k перейдет в непрерывную переменную  – текущую частоту. В результате от ряда Фурье (4) мы перейдем к интегралу, или преобразованию Фурье

.

(6)

Условием существования преобразования Фурье некоторой функции x(t) является ее абсолютная интегрируемость, то есть выполнение неравенства

.

(7)

Комплекснозначная функция X(j), являющаяся преобразованием Фурье сигнала x(t), называется непрерывным спектром (спектральной плотностью) непериодического сигнала. Модуль |X(j)| и аргумент () = arg{X(j)} спектральной плотности называются соответственно амплитудным и фазовым спектрами сигнала. В качестве примера найдем спектральную плотность одиночного прямоугольного импульса длительностью T с амплитудой X₀:

.

Рис. 2. Прямоугольный импульс и его амплитудный и фазовый спектры

На рис. 2 показаны амплитудный и фазовый спектры одиночного прямоугольного импульса. Следует отметить, что в соответствии с определением (6) спектр X(j) действительного сигнала x(t) должен удовлетворять условию эрмитовой сопряженности:

.

По известному спектру X(j) можно восстановить исходный сигнал x(t) с помощью формулы обратного преобразования Фурье:

.

(8)

Перечислим основные свойства спектральной плотности, вытекающие из свойств преобразования Фурье:

1. Линейность. Спектральная плотность взвешенной суммы сигналов равна взвешенной сумме спектральных плотностей этих функций, то есть

.

2. Правило сдвига. Сдвигу сигнала на время t₀ соответствует домножение спектральной плотности на фазовый множитель вида exp(jt₀):

.

3. Производной сигнала соответствует домножение его спектральной плотности на множитель j:

.

4. Спектральная плотность интеграла сигнала равна спектральной плотности сигнала, деленной на j:

.

5. Изменение временного масштаба приводит к обратному изменению масштаба частоты:

.

6. Спектральная плотность произведения сигналов равна свертке их спектральных плотностей, деленной на 2:

.

7. Спектральная плотность свертки сигналов определяется произведением их спектров:

.

Математические модели ряда сигналов, широко используемых в радиотехнике, не удовлетворяют условию абсолютной интегрируемости (примером может служить любой периодический сигнал), поэтому использование преобразования Фурье для определения их спектральных плотностей невозможно. Однако можно говорить о спектральных плотностях таких сигналов, если допустить, что они описываются обобщенными функциями.

Для введения понятия спектральной плотности сигналов, не удовлетворяющих условию абсолютной интегрируемости (7), определим скалярное произведение сигналов как

и найдем связь между скалярными произведениями сигналов и их спектров:

Таким образом, скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей:

.

(9)

Выражение (9) носит название обобщенной формулы Рэлея.

Будем считать, что спектральная плотность Y(j) сигнала y(t), не удовлетворяющего условию (7), является функционалом, который, действуя на известную спектральную плотность X(t) абсолютно интегрируемого сигнала x(t), дает следующий результат:

.

Найдем спектральные плотности сигналов, наиболее часто используемых в радиотехнике (в том числе – не являющихся абсолютно интегрируемыми). Определим спектр -функции, пользуясь ее фильтрующим свойством:

.

Таким образом, спектральная плотность -импульса является константой. В силу симметричности преобразований Фурье ясно, что спектр постоянного сигнала x(t) = A₀ должен представлять собой -функцию, однако, как уже отмечалось, постоянный сигнал не является абсолютно интегрируемым. Рассмотрим произвольный абсолютно интегрируемый сигнал y(t) и воспользуемся обобщенной формулой Рэлея (9):

.

Это равенство может выполняться только в случае, если

.

Физический смысл этого результата очевиден  постоянный сигнал имеет спектральную составляющую только на нулевой частоте.

Вычислим спектр комплексного экспоненциального сигнала вида

,

(10)

воспользовавшись тем же методом. Для произвольного абсолютно интегрируемого сигнала y(t) получим:

.

Отсюда искомая спектральная плотность экспоненциального сигнала выражается как

.

Используя полученное соотношение и формулу Эйлера, легко найти спектральную плотность гармонического сигнала:

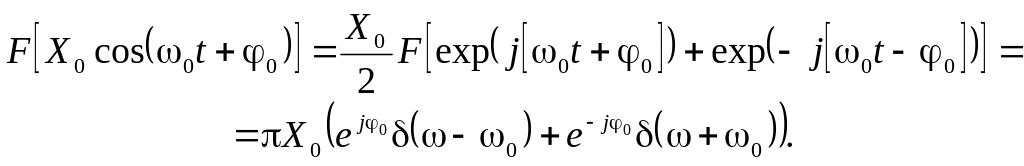
Получив выражение для спектра гармонического сигнала, перейдем к определению спектральной плотности произвольного периодического сигнала x(t) вида (1), предварительно разложив его в ряд Фурье (4):

.