Мода – это ее наиболее вероятное значение

Р_i f (x)

М х М х

Если кривая имеет более одного максимума, то такое распределение называется полимодальным.

х х

Если распределение имеет не максимум, а минимум, то распределение называется антимодальным.

Р_i f (x)

х М х

В общем случае мода и медиана не совпадают, а совпадают только, когда распределение случайной величины – симметрично.

Медиана. Это такое ее значение М_е для которого

т.е. одинаково вероятно, окажется случайная величина меньше или больше М_е.

Г еометрическая интерпретация:

S₁ = S₂

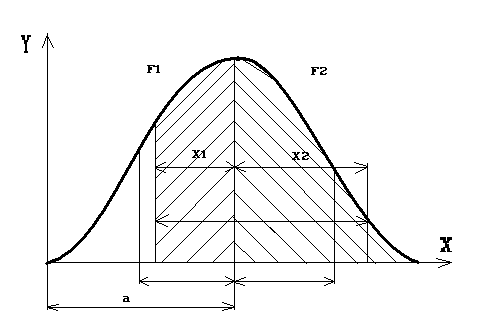
Медиана это абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

4.3.3. Моменты. Дисперсия и среднеквадратичное отклонение.

Центрированная случайная величина – отклонение случайной величины х от ее математического ожидания.

(4.7)

Математическое ожидание центрированной случайной величины равно нулю.Действительно

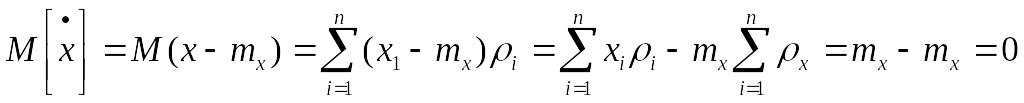
Очевидно, центрирование случайной величины равносильно переносу начала координат в среднюю точку, абсцисса которой равна математическому ожиданию.

Моменты центрированной случайной величины носят название центральных моментов.

Рассмотрим второй центральной момент.

(4.8)

Относительно произвольно выбранной абсциссы со значением а. Преобразуем это выражение.

при а = m_x – полученная величина достигает минимума. Таким образом второй центральный момент из всех вторых моментов является минимальным.

В виду особой важности ему присвоили специальное название – дисперсия (с английского - разброс) и обозначают следующим образом.

Для непосредственного вычисления дисперсии применяют формулы:

_(4.9)

Дисперсия характеризует рассеяния случайной величины относительно математического ожидания. Она имеет размерность квадрата случайной величины. Для того, чтобы пользоваться дисперсией имеющей ту же размерность из нее извлекают квадратный корень

(4.10)

Которое называют среднеквадратичным отклонением. Для упрочнения записи среднеквадратичное отклонение и дисперсию обозначают через σ_х, Д_х.

Третий центральный момент. Служит для характеристики асимметрии распределения. Действительно в сумме

(4.11)

При суммарном относительно m_x законе распределения и нечетном S, каждому положительному значению слагаемого соответствует равное ему по абсолютной величине отрицательное слагаемое, поэтому вся сумма равна нулю, что то же самое справедливо и для интеграла

(4.12)

как интеграл в симметричных пределах от нечетной функции. При малейшем отклонении от симметрии, как сумма, так и интеграл будут иметь значения отличные от нуля.

Естественно, в качестве характеристики асимметрии принять один из нечетных моментов. Простейшие из них имеют размерность куба. Чтобы получить безразмерный коэффициент асимметрии значение μ₃ делят на куб среднеквадратичного отклонения.

(4.13)

f (x)

m₁ m₂ x

1 – положительная асимметрия S_k>0;

2 – отрицательная асимметрия S_k<0.

Четвертый центральный момент – определяет крутость или островершинность. Эти свойства описываются коэффициентом называемым эксцессом.

f(x)

m_x х

число 3 вычитается потому, что для нормального распределения величина

Многочисленные исследования показали, что в технологии машиностроения распределение размеров чаще всего происходит по нормальному закону или закону Гаусса.

Она является результатом действия большого числа различных факторов с одинаковой по интенсивности своего влияния, этому закону подчиняются многие непрерывные случайные величины: размеры деталей, обработанных на настроенных станках; вес заготовок и деталей машин; твердость и другие характеристики механических свойств материала; высота микронеровностей на обработанных поверхностях; погрешности измерений и другие величины.

Кривая Гаусса выражается следующим уравнением:

(4.14);

где  - среднее квадратическое отклонение аргумента; е – основание натуральных логарифмов; a – значение абсциссы, при которой ордината y кривой достигает max.

Величина, а является центром распределения (группирование) аргумента и в тоже время его средней арифметической.

Закон Гаусса двухпараметрический (параметр  и а).

Ординаты вершины кривой x=а

Точки перегиба кривой лежат на расстояниях  от ее оси симметрии. Их ординаты

-

Величина среднего квадратичного отклонения , являющаяся мерой точности характеризует форму кривой распределения. При малых значениях  точность исследуемого метода повышается и кривая получается сильно вытянутой вверх с малым полем рассеяния. При больших значениях  кривая получается очень пологой и поле рассеяния растет.

Определение  по результатам измерений производится по следующей формуле

, (4.15)

где n-количество произведенных измерений (рекомендуется брать равным 50)

x_i- значение текущего измерения;

x_ср- среднее арифметическое из произведенных измерений;

, (4.16)

Геометрически кривая нормального распределения простирается в обе стороны вдоль оси абсцисс беспредельно, асимптотически приближаясь к этой оси, как это видно из рис.

Для теоретических расчетов предельные отклонения (при использовании нормального закона рассеяния), выражаемое в долях среднеквадратического отклонения (x), ограничивают обычно величинами x=3.

При этих значениях x; 99,73% отклонений случайной величины попадают в область внутри установленных пределов и 0,27% выходят из них.

Таким образом, вычислив по данным наблюдений значение , можно охарактеризовать точность исследуемого метода произведением 6. В этом случае мы имеем практически 100-процентную годность обрабатываемых деталей, т.к. вероятное количество брака менее 0,3%.

Кроме закона Гаусса встречаются другие законы распределения размеров обрабатываемых деталей в партии.

Если на выполняемый размер оказывает влияние систематическая равномерно возрастающая погрешность (погрешность, вызываемая размерным износом режущего инструмента) протекающая по закону прямой, то распределение происходит по закону равной вероятности.

Если на выполняемый размер влияет закономерно изменяющаяся погрешность, возрастающая сперва замедленно, а затем ускоренно, то распределение размеров проходит по закону треугольника (Симпсона).

Это распределение может иметь место при совместном действии размерного износа режущего инструмента с сильно выраженной фазой начального износа и увеличения силы резания в конце стойкости инструмента в результате его прогрессирующего затупления.

Рассмотрим кривые распределения погрешностей взаимного положения и погрешностей формы поверхностей обработанных деталей. Эти погрешности являются положительными величинами, они изменяются от нуля до определенного значения. Кривая распределения эксцентриситетов R ступенчатых цилиндрических деталей имеет несимметричную форму.

Закон эксцентриситета (закон Релея)

Характер изменения кривой говорит о том, что деталей с нулевым эксцентриситетом нет; большая часть деталей имеет средний по величине эксцентриситет; деталей с большим эксцентриситетом имеется мало.

Закону эксцентриситета (закону Релея) следует также распределение значений непараллельности и неперпендикулярности двух плоскостей; неперпендикулярность оси детали к ее торцовой поверхности; разностенность полых деталей (при нефиксированной плоскости измерения). Этот закон однопараметрический. Среднеарифметическое значение X_cp эксцентриситетов R связано со среднеквадратичным отклонением постоянным соотношением

Х_ср=1,92.

Систематическая постоянная погрешность не оказывает влияния на форму кривой распределения. Влияние этой погрешности сказывается лишь в том, что кривая распределения сдвигается вправо на величину с этой погрешности.

Если на ряду со случайными имеются и систематические закономерно изменяющиеся погрешности, то кривая распределения искажается. Так в качестве примера показана кривая, представляющая собой композицию кривой Гаусса и кривой равномерной вероятности. Эта кривая может получиться в том случае, когда на точность обработки оказывает сильное влияние размерный износ инструмента.

Кривая распределения для двух одинаковых партий деталей, обработка которых производится при двух различных настройках станка, получается двухвершинной. Для нескольких настроек может получиться многовершинная кривая.

При большом количестве настроек многовершинность сглаживается и кривая приобретает форму кривой нормального распределения, но с более широкой базой. Увеличение ширины базы происходит на величину погрешности настройки _н.

Статический метод исследования на базе кривых распределения дает возможность объективно оценить точность различных способов механической обработки. Данный метод универсален. Его можно применить для исследования точности выполнения заготовок, сборочных операций, операций технического контроля, а также для целого ряда таких специфических операций, как балансировка, холодная правка и пр.. Он особенно удобен (а часто и незаменим) в тех случаях, когда механизм явления не изучен. Целесообразно применять его также для практической проверки результатов и выводов, полученных на основе расчетно-аналетического метода.

К существенным недостаткам этого метода относится, то, что он не вскрывает сущность физических явлений и фактов, влияющих на точность обработки, а также то, что на его базе не выявляются конкретные возможности повышения точности. Метод фиксирует результаты законченного этапа, т.е. «обращен в прошлое». Полученные ранее значения  не могут быть использованы, если в условиях выполнения данной операции произошли изменения (режим резания, способ установки заготовки и т.п.). В этом случае необходимо определить новое значение .