2. Поиск в ширину в графе

Теперь рассмотрим несколько иной метод поиска в графе, называемый поиском в ширину. Прежде чем описать его, отметим, что при поиске в глубину чем позднее будет посещена вершина, тем раньше она будет использована - точнее, так будет при допущении, что вторая вершина посещается перед использованием первой. Это прямое следствие того факта, что просмотренные, но еще не использованные вершины накапливаются в стеке. Поиск в ширину основывается, грубо говоря, на замене стека очередью. После такой модификации чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью просмотра всех еще непросмотренных соседей этой вершины. Вся процедура представлена ниже:

1 procedure ПОИCК_В_ШИРИНУ_В_ГРАФЕ (v);

{поиск в ширину в графе с началом в вершине v;

переменные НОВЫЙ, СПИСОК - глобальные}

2 begin

3 ОЧЕРЕДЬ := ; ОЧЕРЕДЬ  v; НОВЫЙ [v] := ложь;

4 while ОЧЕРЕДЬ   do

5 begin p  ОЧЕРЕДЬ; посетить p;

6 for u  ЗАПИСЬ [ p] do

7 if НОВЫЙ [ u] then

8 begin ОЧЕРЕДЬ  u; НОВЫЙ [ u ] := ложь

9 end

10 end

11 end {вершина v использована}

Способом, аналогичным тому, который был применен для поиска в глубину, можно легко показать, что вызов процедуры ПОИCК_В_ШИРИНУ_ В_ГРАФЕ (v) приводит к посещению всех вершин связной компоненты графа, содержащей вершину v, причем каждая вершина просматривается в точности один раз. Вычислительная сложность алгоритма поиска в ширину также имеет порядок m+n, так как каждая вершина помещается в очередь и удаляется из очереди в точности один раз, а число итераций цикла 6, очевидно, будет иметь порядок числа ребер графа.

Рис. 3. 4.

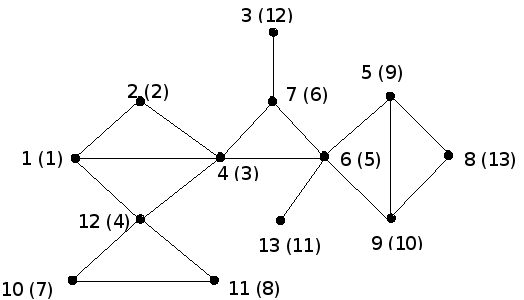
На рис. 3.4 представлен граф, вершины которого занумерованы (в скобках) согласно очередности, в которой они посещаются в процессе поиска в ширину.

Как и в случае поиска в глубину, процедуру ПОИCК_В_ШИРИНУ_ В_ГРАФЕ (v) можно использовать без всяких модификаций и тогда, когда список инцидентности СПИСОК [ v ], v  V, определяет некоторый ориентированный граф. Очевидно, что тогда посещаются только те вершины, до которых существует путь от вершины, с которой мы начинаем поиск.

4. Пути и циклы

Путем в ориентированном или неориентированном графе G = <V, E> называют последовательность ребер вида <(v₁ ,v₂ ), (v₂ , v₃ ), ...(v_n-1 ,v_n)> = S = <E₁ , ... , E_n-1 >, где E_i = (v_i , v_i+1) E, E_i и E_i+1 инцидентны одной вершине. Говорят, что этот путь идет из v₁ в v_n и имеет длину n - 1. Часто такой путь представляют последовательностью вершин < v₁ , ... , v_n > , <v_i ,v_i+1 > E , лежащих на нем. В вырожденном случае одна вершина обозначает путь длины 0, идущий из этой вершины в нее же.

Путь называется простым, если все ребра и все вершины на нем, кроме быть может первой и последней, различны.

Цикл - это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине. Заметим, что в неориентированном простом графе длина цикла должна быть не менее 3.

Оба вида поиска в графе - в глубину и в ширину - могут быть использованы для нахождения пути между фиксированными вершинами v и u. Достаточно начать поиск в графе с вершины v и вести его до момента посещения вершины u. Преимуществом поиска в глубину является тот факт, что в момент посещения вершины u стек содержит последовательность вершин, определяющих путь из v в u. Это становится очевидным, если отметить, что каждая вершина, помещаемая в стек, является смежной с верхним элементом стека. Однако недостатком поиска в глубину является то, что полученный таким образом путь в общем случае не будет кратчайшим путем из v в u.

От этого недостатка свободен метод нахождения пути , основанный на поиске в ширину. Модифицируем процедуру ПОИCК_В_ШИРИНУ_В_ГРА ФЕ, заменяя строки 7-9 на

if НОВЫЙ [ u ] then

begin ОЧЕРЕДЬ  u; НОВЫЙ [ u ] := ложь

ПРЕДЫДУЩИЙ [ u ] :=p

end

По окончании работы модифицированной таким образом процедуры массив ПРЕДЫДУЩИЙ содержит для каждой просмотренной вершины u вершину ПРЕДЫДУЩИЙ[u], из которой мы попали в u. Отметим, что кратчайший путь из вершины u в вершину v обозначается последовательностью вершин u = u₁, u₂, ... u_k=v, где u_i+1 = ПРЕДЫДУЩИЙ [u_i] для 1  i < k и k является первым индексом i для которого u_i = v. Действительно, в очереди помещены сначала вершины, находящиеся на расстоянии 0 от v (т.е. сама вершина v), затем поочередно все новые вершины, находящиеся на расстоянии 1 от v, и т.д. Под расстоянием здесь мы понимаем длину кратчайшего пути. Предположим теперь, что мы уже рассмотрели все вершины, находящиеся на расстоянии, не превосходящем r от v, что очередь содержит все вершины, находящиеся на расстоянии r от v, и только эти вершины и что массив ПРЕДЫДУЩИЙ правильно определяет кратчайший путь от каждой, уже просмотренной вершины до вершины v способом, описанным выше. Использовав каждую вершину p, находящуюся в очереди, наша процедура просматривает некоторые новые вершины, и каждая такая новая вершина u находится на расстоянии r + 1 от v, причем, определяя ПРЕДЫДУЩИЙ [u] := p, мы продлеваем кратчайший путь от p до v до кратчайшего пути от u до v. После использования всех вершин из очереди, находящихся на расстоянии r от v, она (очередь), очевидно, содержит множество вершин, находящихся на расстоянии r+1 от v, и легко заметить, что условие индукции выполняется и для расстояния r+1.