
matan
.pdf
где интеграл в правой части берется с помощью рекуррентной формулы(4.24).
В заключение этого пункта методом Лагранжа получим следующую формулу
|
∫ |
|
|
dx |
|
= |
1 |
|
a + x |
|
+C . |
|
|
|
|
|
|
ln |
|
|
|||||||
a |
2 |
|
2 |
2a |
a − x |
|
|||||||
|
|
− x |
|
|
|
|
|
||||||
Для этого заметим, |
|
что |
|
подынтегральную |
правильную |
||||||||
рациональную дробь |
|
|
1 |
|
|
можем представить в |
виде суммы |
||||||
a2 |
− x2 |
|
|
||||||||||
простейших правильных рациональных дробей с неопределенными коэффициентами А и В.
∫ |
|
dx |
|
= |
|
1 |
|
= |
A |
+ |
B |
= |
(A − B)x +aA +aB. |
|||
a |
2 |
2 |
( |
)( |
) |
|
|
|||||||||
|
− |
x |
|
|
|
a − x a + x |
( |
)( |
) |
|||||||
|
|
|
|
|
a − x a + x |
|
|
a − x a + x |
|
|||||||
Отсюда
0 х+1=(A-B) х + aA + aB
идля определения A и В приходим к системе линейных уравнений
xA − B = 0,
x0 aA + aB =1.
Решая последнюю, получим
A=B= 2a1 .
Тогда имеем
∫ |
|
|
dx |
|
= |
1 |
|
∫ |
dx |
+ ∫ |
dx |
|
= |
1 |
(−ln |
|
a − x |
|
+ ln |
|
a + x |
|
)= |
1 |
ln |
|
a + x |
|
+ C. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
a |
− x |
|
2a |
|
a − x |
a + x |
|
2a |
|
|
|
|
2a |
|
|
a − x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда, как следствие, можно получить и формулу
∫x2dx−a 2 = 2a1 ln aa −+ xx + C.
4.6.Интегрирование тригонометрических выражений
Впункте 1.4.5 мы установили, что интеграл от любой рациональной дроби представляет собой элементарную функцию. В настоящем пункте и далее мы рассмотрим другие классы функций, которые также интегрируются в элементарных функциях. Как правило,
131

мы с помощью определенной подстановки будем сводить интеграл к интегралу от рациональной дроби.
Определение 4.6. Рациональной функцией R(x,y) от двух аргументов x и у называется отношение вида
R(x, y) = Pn (x, y) ,
Qm (x, y)
где Pn(x,y) и Qm(x,y) являются многочленами степени n и m с действительными коэффициентами относительно двух аргументов х и у, т.е.
Pn(x,y)=a00+a10x+a01y+a20x2+a11xy+a02y2+...+a0nyn,
Qm(x,y)=b00+b10x+b01y+b20x2+b11xy+b02y2+...+b0mym.
Теперь перейдем к рассмотрению интегралов от функций вида
R(cos x,sin x), т.е. к интегралам
∫R (cos x, sin x)dx. |
(4.43) |
Для вычисления подобных интегралов делаем подстановку
t = tg |
π |
,−π < x < π. |
(4.44) |
|
2 |
|
|
x=2arctg t, dx = 12+dtt 2 .
Теперь используя известные тригонометрические формулы
|
2tg |
x |
|
|
|
|
|
|
1 − tg2 |
x |
|
||||||
|
|
|
2 |
|
|||||||||||||
sin x = |
|
|
|
2 |
|
|
|
|
и cosx = |
|
|
|
|
|
|
||
|
|
|
|
|
x |
|
|
1 + tg2 |
x |
|
|||||||
1 + tg2 |
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
и учитывая(4.44), получим |
|
|
|
|
|
|
|
|
|
|
|
|
− t 2 |
|
|
|
|
sin x = |
|
|
2t |
|
|
и cosx = |
1 |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
+ t 2 |
|
1 |
|
|
||||||||||||
|
|
|
|
+ t 2 |
|
|
|||||||||||
Тогда исходный интеграл(4.43) превращается в следующий
132
|
2t |
|
|
1 − t |
2 |
|
2dt |
|
||
∫R(cos x, sin x)dx = ∫R |
|
|
, |
|
|
. |
||||
|
|
|
|
|
|
|
||||
|
+ t |
2 |
1 + t |
2 |
2 |
|||||
1 |
|
|
|
1 + t |
||||||
Так как рациональная функция от рациональной функции также является рациональной функцией, то стоящий справа в (4.45) интеграл есть интеграл от рациональной дроби, который умеем интегрировать
(см. пункт 1.4.5).
Заметим далее, что хотя (4.44) является универсальной подстановкой, но иногда приводит к громоздким вычислениям. Поэтому в некоторых частных случаях подынтегральной функции R(cos x,sin x) в (4.43) удобнее пользоваться другими подстановками.
Рассмотрим эти частные случаи.
1. Пусть рациональная функция R(cos x,sin x) в(4.43) меняет знак при изменении знака одного из аргументов, т.е.
R(-cos x/sin x)=-R(cos x,sin x) или R(cos x ,-sin x)=-R(cos x,sin x).
Тогда удобнее сделать подстановки
sin x=t или cos x=t. (4.45)
2. Пусть рациональная функция R(cos x,sin x) в(4.43) не меняет своего значения при одновременном изменении знаков cos x и sin x, т.е.
R(-cos x,-sin x)=R(cos x,sin x).
Тогда удобнее пользоваться подстановкой
t=tg x, |
− |
π |
< x < |
π |
|
|
|
|
(4.46) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
c учетом того, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = arctgt,dx |
= |
|
|
dt |
|
,cos2 |
x = |
|
1 |
= |
|
|
1 |
, sin 2 x = |
|
|
tg2x |
= |
|
|
t 2 |
. |
|||
1 |
+ t 2 |
1 + tg2x |
1 |
+ t 2 |
1 |
+ tg2x |
1 |
+ t 2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
В заключение этого пункта еще раз напомним, что некоторые рекуррентные формулы, связанные с интегрированием тригонометрических функций, нами получены в пункте 1.4.5 методом интегрирования по частям. Ими также часто пользуются при вычислении интегралов от тригонометрических функций.
133

4.7. Интегрирование дробно-линейных иррациональностей и дифференциальных биномов
Рассмотрим интегралы вида
где R x, n
линейной
|
|
|
|
|
a |
x + b |
|
|
|
|||
|
|
|
|
∫R x, n |
1 |
|
1 |
dx, |
||||
|
|
|
|
|
a 2x + b2 |
|
||||||
a |
x + b |
|
|
есть рациональная |
|
|||||||
1 |
|
1 |
|
|
||||||||
a 2x + b2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
иррациональностиn |
a1x + b1 |
, |
|||||||||
|
a 2x + b2 |
|
|
|||||||||
(4.47)
функция от х и от дробно-
a1, b1, a2, b2-некоторые
действительные постоянные, n- целое положительное число.
Покажем, что при условии a1b2-a2b1≠0 интеграл (4.47) можно вычислить подстановкой
a1x + b1 |
|
t= n a 2x + b2 . |
(4.48) |
На самом деле, так как из(4.48) следует, что
x = b2t n − b1 a1 −a 2t n
и |
|
|
|
|
|
|
|
|
|
|
|
||
dx = |
b2nt n −1 (a1 −a 2t n )−a 2nt n −1 (b2t n − b1 ) |
dt = |
n(a1b2 −a 2b1 ) t n |
dt , |
|||||||||
|
|
|
|
|
(a1 −a 2t n )2 |
|
|
(a1 −a 2t n )2 |
|||||
|
|
|
|
|
|
|
|
|
|
||||
то(4.47) примет вид |
|
|
|
|
|
|
|
|
|
||||
|
b |
2 |
t n |
− b |
n(a1b2 −a 2b1 )t n |
(4.49) |
|
||||||
|
∫R |
|
|
|
1 |
, t |
|
|
dt |
|
|||
|
|
|
|
|
n |
|
n 2 |
|
|||||
|
a1 −a 2t |
|
|
(a1 −a 2t |
) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
и мы приходим к интегралу от дробно рациональной функции, интегрировать которую мы умеем(см. пункт 1.4.5).
Теперь перейдем к вопросу интегрирования дифференциальных биномов.
Определение 4.7. Дифференциальным биномом называется дифференциальное выражение вида
134

xm(a+bxn)pdx, |
(4.50) |
где а,b- произвольные действительные постоянные.
Еще в середине прошлого столетия известным математиком Чебышевым было доказано, что интегралы от дифференциальных биномов, т.е. интегралы вида
∫xm (a + bxn )p dx, |
(4.51) |
рационализируются только в трех случаях значений m, n, p.
Рассмотрим эти случаи по отдельности: 1. p- целое число
Вэтом случае для вычисления (4.51) можно пользоваться двумя
способами. Или вводим новую переменную t= r x , где r есть общий знаменатель дробей m и n, или просто возведя a+bxn в целую степень p, приходим к сумме интегралов от степенных функций.
x , где r есть общий знаменатель дробей m и n, или просто возведя a+bxn в целую степень p, приходим к сумме интегралов от степенных функций.
2.mn+1 - целое число
Вэтом случае интеграл (4.51) вычисляется подстановкой
a+b xn=tν , |
(4.52) |
|
где ν- знаменатель дроби p = |
s |
. |
|
||
|
ν |
|
3. mn+1 + p - целое число
В этом случае интеграл(4.51) вычисляется подстановкой a+bxn=tν xn,
где ν- знаменатель дроби p = νs .
Заметим, что во всех остальных случаях значений чисел m, n, p, не совпадающих с выше разобранными случаями, для вычисления интеграла(4.51) требуется применение приближенных или численных методов интегрирования.
4.8. Интегрирование квадратичных иррациональностей. Подстановки Эйлера
Рассмотрим интеграл вида
135

∫R (x, ax2 |
+ bx +d )dx, |
(4.53) |
где R(x, ax2 + bx +d ) есть |
рациональная |
функция от независимой |
переменной х и от квадратичной иррациональности
 ax2+bx+d ≥0, a, b, d- действительные постоянные числа.
ax2+bx+d ≥0, a, b, d- действительные постоянные числа.
Отметим, что если у квадратного трехчлена ax2+bx+d равные
действительные корни и а>0, то иррациональность 
 ax2 + bx +d заменяется рациональным выражением и для рационализации интеграла(4.53) не требуется никакой подстановки.
ax2 + bx +d заменяется рациональным выражением и для рационализации интеграла(4.53) не требуется никакой подстановки.
А если у квадратного трехчлена ax2+bx+d нет равных действительных корней, то для вычисления интеграла (4.53) необходимо пользоваться известными тремя подстановками Эйлера. Рассмотрим их по отдельности.
1. Первая подстановка Эйлера.
Пусть квадратный трехчлен ax2+bx+d не имеет действительных корней(D=b2-4ad<0) и a>0.
В этом случае интеграл (4.53) вычисляется первой подстановкой Эйлера
|
|
|
|
|
|
|
|
|
|
|
|
ax2 |
+ bx +d =t- |
a |
x , |
(4.54) |
|||
или |
|
|
|
|
|
|
|
||
|
ax2 |
+ bx +d |
=t+ |
|
|
x . |
(4.55) |
||
|
|
a |
|||||||
Возведя обе части (4.54) в квадрат

 ax2 + bx +d = t 2 −2
ax2 + bx +d = t 2 −2
 a tx +ax2
a tx +ax2
и решая относительно х, получим
x = 2 a t + b . (4.56)
Нетрудно заметить, что при этом
dx = 2 |
a t 2 |
+ bt +d |
a |
dt. |
(4.57) |
|
(2 |
a t + b)2 |
|
||||
ax2 + bx +d = |
a t 2 |
+ bt +d |
a . (4.58) |
|||
|
|
2 |
a + b |
|
||
136

Тогда с учетом (4.56),(4.57),(4.58) подынтегральное выражение в (4.53) принимает вид
|
t 2 −d |
|
a t 2 + bt +d a 2( a t 2 + bt +d a ) |
|
|||
∫R |
2 a t + b |
, |
2 a t + b |
|
(2 a t + b) |
2 |
dt. |
|
|
|
|
|
|||
Отметим, что подстановка(4.55) приведет нас к аналогичному результату.
2. Вторая подстановка Эйлера.
Если квадратный трехчлен ax2+bx+d не имеет действительных корней (D=b2-4ad<0) и d > 0, то интеграл(4.53) вычисляется второй подстановкой Эйлера:
|
|
|
|
|
|
|
|
|
ax2 |
+ bx +d =xt- |
d |
, |
(4.59) |
||
или |
|
|
|
|
|
|
|
|
|
|
=xt+ |
|
. |
(4.60) |
|
|
ax2 |
+ bx +d |
|||||
|
d |
||||||
Если возвести обе части (4.59) в квадрат, то получим
ax2+bx+d=x2t2-2 
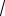 d tx+d.
d tx+d.
Отсюда следует, что
x = b +2 dt , t 2 −a
dt , t 2 −a
dx = −2 a  d + bt dt,
d + bt dt,
(t 2 −a )2
|
= |
dt 2 + bt + da |
|
ax2 + bx +d |
|||
t 2 −a |
|||
|
|
(4.61)
(4.62)
(4.63)
Теперь с учетом(4.61), (4,62), (4,63) интеграл принимает вид
b +2 dt |
|
dt 2 + bt + da bt +a d |
|
||||||||
-2 ∫R |
|
2 |
|
, |
|
2 |
|
|
|
|
dt. |
t |
−a |
t |
−a |
(t 2 −a ) |
2 |
||||||
|
|
|
|
|
|
|
|||||
Подстановка(4.60) приводит к аналогичному результату. 3. Третья подстановка Эйлера.
137


Примеры
Пример 1. Вычислить
|
|
|
|
|
|
∫ |
(2 3 |
x + 1)ln (3 |
x + 2 )dx , x>0. |
|
(4.68) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
33 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решение: Заменяя, что |
|
dx |
|
= d 3 |
|
|
|
и введя новую переменную по |
||||||||||||||||||
|
|
|
|
|
|
x |
|||||||||||||||||||||||
|
|
|
|
|
x 2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
формуле 3 x = y , (4.68) перепишем в виде |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
∫(23 |
x +1) ln(3 |
x + 2)d3 |
x = ∫(2 y +1) ln( y + 2)dy . |
(4.69) |
|
|||||||||||||||||||
|
|
|
Интеграл (4.69), вычислим методом интегрирования по частям, взяв |
||||||||||||||||||||||||||
U = ln( y + 2), dU = |
|
dy |
и dV = (2 y +1)dy, V = y2 |
+ y . |
|
||||||||||||||||||||||||
y + 2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Тогда, согласно (4.19), имеем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
∫(2 y +1) ln( y + |
2)dy = ( y 2 |
|
+ y) ln( y + 2) − ∫ |
y 2 |
+ y |
dy . |
(4.70) |
|||||||||||||||||
|
|
|
|
y + 2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Второй член в правой части (4.70) представляет собой |
||||||||||||||||||||||||||
неопределенный |
|
интеграл |
от |
|
неправильной |
рациональной дроби |
|||||||||||||||||||||||
|
y 2 |
+ y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выделяя в этой дроби целую часть (см. пункт 4.5.) и представляя |
||||||||||||||||||||||||||
ее |
в |
|
виде |
|
y 2 |
|
+ y |
|
= y − 1 + |
|
|
2 |
|
, |
|
после |
вычисления |
интеграла |
|||||||||||
|
|
y + 2 |
|
y |
+ |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫ |
y 2 |
+ y |
dy = |
y 2 |
− y + 2 ln( y + 2) + C, из (4.70) получим |
|
|
||||||||||||||||||||||
y + 2 |
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
∫(2 y +1) ln( y + 2)dy = ( y 2 + y) ln( y + 2) − |
y 2 |
+ y − 2 ln( y + 2) + C . |
(4.71) |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Теперь остается перейти к переменной x в (4.71).
Ответ:
139

∫ |
(23 |
x +1) ln(3 x + 2) |
dx = (3 x 2 + 3 |
x − 2) ln(3 |
x + 2) − |
1 |
3 x2 |
+ 3 x + C. |
|
33 x 2 |
2 |
Пример 2. Вычислить
|
|
|
|
∫ |
tg |
|
x |
sin x(1 + cos x)dx , 0 ≤ x ≤ |
π . |
(4.72) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
sin x +1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
Решение: Применяя подстановку (4.44) с учетом x = 2arctgt, |
dx = |
|||||||||||||||||||||||||||
2dt |
|
, sin x = |
|
|
2t |
|
, cos x = |
|
1 −t 2 |
получим |
|
|
|
|
|
|
|
|
|||||||||||
1 +t 2 |
1 |
+t 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 +t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
1−t |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
||
|
|
x |
sinx(1+cosx) |
|
|
|
|
1+t |
2 |
|
1+t |
2 |
|
2dt |
|
tdt |
|
||||||||||||
∫ tg |
dx=∫ |
t |
|
|
|
|
|
|
|
|
=4∫ |
|
|||||||||||||||||
2 |
sinx +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(4.73) |
||||||||||||
|
|
|
|
|
|
|
2t |
|
+1 |
|
|
1+t2 |
(t +1)2 (t2 +1) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+t2 |
|
|
|
|
|
|
|
|
|||||||
|
Подынтегральная |
|
|
функция |
|
в |
(4.73) |
является правильной |
|||||||||||||||||||||
рациональной дробью относительно переменной t. Представим ее в виде суммы простейших правильных дробей методом Лагранжа (см. (4.35)).
Имеем |
|
|
|
|
|
|
|
|
|
|
|
t |
= |
A |
|
+ |
B |
+ |
Et + D |
, |
(4.74) |
|
(t +1)2 (t 2 +1) |
t + |
1 |
(t +1)2 |
t 2 +1 |
|||||
|
|
|
|
|
|
|||||
что приводит к системе линейных уравнений для определения неопределенных коэффициентов A, B, E, D:
t3 |
A + B = 0, |
|
|
t 2 |
A + B + 2E + D |
= 0, |
(4.75) |
t |
A + E + 2D =1, |
|
|
t 0 |
A + B + D = 0. |
|
|
Решая систему (4.75), получим А=0, В = − 12 , Е = 0, D = 12 . Тогда вместо интеграла (4.73) будем иметь
140
