Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Волгоградский государственный технический университет» Кафедра «Высшая математика» криволинейные интегралы

Методические указания

Волгоград

2011

УДК 517.373(075)

Рецензент:

старший преподаватель кафедры «Прикладная математика» Н.И. Кольцова

Печатается по решению редакционно-издательского совета

Волгоградского государственного технического университета

Криволинейные интегралы : метод. указания / сост. М.И.Андреева,

О.Е. Григорьева; ВолгГТУ. – Волгоград, 2011. – 26 с.

Методические указания являются руководством к выполнению индивидуальных заданий по теме « Криволинейные интегралы и их приложения к теории поля».

В первой части методических указаний содержится необходимый теоретический материал для выполнения индивидуальных заданий.

Во второй части рассмотрены примеры выполнения всех типов заданий, включенных в индивидуальные задания по теме, что способствует лучшей организации самостоятельной работы студентов и успешному усвоению темы.

Методические указания предназначены для студентов первого и второго курсов.

© Волгоградский государственный

технический университет, 2011

1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 1 РОДА

Определение криволинейного интеграла 1 рода

Пусть АВ– дуга плоской или пространственной кусочно-гладкой кривойL,f(P) – заданная на этой дуге непрерывная функция,А₀=А,А₁,А₂, …,А_{n – 1},А_n=B– произвольное разбиение дугиАВиP_i– произвольные точки на частичных дугахА_{i – 1}A_i, длины которыхl_i(i= 1, 2, …,n). Тогда существует предел последовательности интегральных сумм

при nи maxl_i0, который не зависит ни от способа разбиения дугиАВточкамиA_i, ни от выбора точекP_iна частичных дугахА_{i – 1}A_i(i= 1, 2, …,n). Этот предел называется криволинейным интегралом 1 рода от функцииf(P) по кривойLи обозначается

или .

Вычисление криволинейного интеграла 1 рода

Вычисление криволинейного интеграла 1 рода может быть сведено к вычислению определенного интеграла при разных способах задания кривой интегрирования.

Параметрическое задание кривой интегрирования

Если дуга АВплоской кривой задана параметрически уравнениямигдеx(t) иy(t) – непрерывно дифференцируемые функции параметраt, причемx(t₁) =x_A,x(t₂) =x_B, то

(1.1)

где - дифференциал длины дуги кривой.

Аналогичная формула имеет место в случае параметрического задания пространственной кривой L. Если дугаАВ кривой L задана уравнениями, иx(t),y(t),z(t) – непрерывно дифференцируемые функции параметраt, то

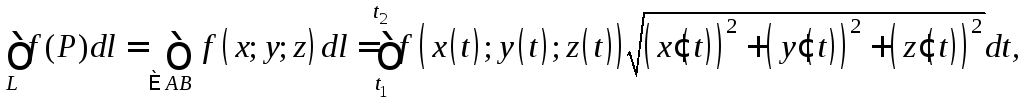(1.2)

где - дифференциал длины дуги кривой.

Явное задание плоской кривой интегрирования

в декартовых координатах

Если дуга АВплоской кривойLзадана уравнениемгдеy(x) – непрерывно дифференцируемая функция, то

и формула для вычисления криволинейного интеграла имеет вид:

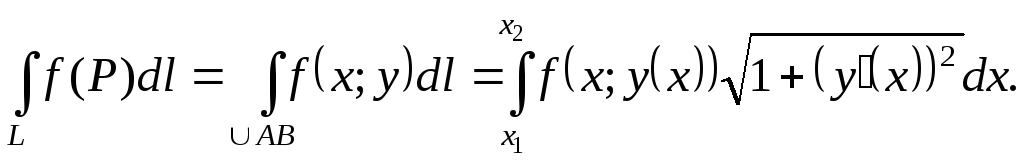(1.3)

При задании дуги АВплоской кривойLв видеx =x(y),y[y₁;y₂], гдеx(y) – непрерывно дифференцируемая функция,

и криволинейный интеграл вычисляется по формуле

(1.4)

Задание кривой интегрирования полярным уравнением

Если плоская кривая Lзадана уравнением в полярной системе координатr=r(),[₁;₂], гдеr() – непрерывно дифференцируемая функция, то

и

(1.5)

Приложения криволинейного интеграла 1 рода

С помощью криволинейного интеграла 1 рода вычисляются: длина дуги кривой, площадь части цилиндрической поверхности, масса, статические моменты, моменты инерции и координаты центра тяжести материальной кривой с заданной линейной плотностью.

1. Длина lплоской или пространственной кривойL находится по формуле

(1.6)

2. Площадь части цилиндрической поверхности с параллельной оси OZобразующей и расположенной в плоскостиXOYнаправляющейL, заключенной между плоскостьюXOYи поверхностью, задаваемой уравнениемz=f(x;y) (f(P)0 приPL), равна

(1.7)

3. Масса mматериальной кривойLс линейной плотностью(P) определяется формулой

(1.8)

4. Статические моменты относительно осей OxиOyи координаты центра тяжести плоской материальной кривойL с линейной плотностью(x;y) соответственно равны:

(1.9)

(1.10)

5. Статические моменты относительно плоскостей Oxy,Oxz,Oyzи координаты центра тяжести пространственной материальной кривой с линейной плотностью(x;y;z) определяются по формулам:

(1.11)

(1.12)

6. Для плоской материальной кривой Lс линейной плотностью(x;y) моменты инерции относительно осейOx,Oyи начала координат соответственно равны:

(1.13)

7. Моменты инерции пространственной материальной кривой Lс линейной плотностью(x;y;z) относительно координатных плоскостей вычисляются по формулам

(1.14)

а моменты инерции относительно координатных осей равны:

(1.15)