
- •Теория вероятностей (для студентов специальности «Информатика») Тема 2. Повторные независимые испытания
- •§1. Формула Бернулли.
- •§2. Формула Пуассона.
- •§3. Локальная и интегральная теоремы Муавра-Лапласа.
- •Тема 3. Случайные величины
- •§8. Закон равномерного распределения вероятностей.
- •§9. Определение показательного распределения.
- •§10. Вероятность попадания в заданный интервал показательно распределенной случайной величины.
- •§12. Числовые характеристики показательного распределения.
- •§11. Геометрические вероятности
- •§12. Предмет метода Монте − Карло
- •§13. Понятие о законе больших чисел.
- •§14. Понятие о теореме Ляпунова. Формулировка центральной предельной теоремы
- •Тема 4. Выборочный метод
- •§1. Статистическое распределение выборки
- •§2. Эмпирическая функция распределения
- •§3. Полигон и гистограмма
- •Тема 5. Статистические оценки параметров распределения
- •§1. Точечные оценки
- •§2. Метод моментов
- •§3. Метод наибольшего правдоподобия
- •§4. Интервальные оценки
- •Тема 6. Оценка независимой вероятности событий по частоте
- •§1. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •§2. Проверка гипотезы о показательном распределении генеральной совокупности
- •§3. Проверка гипотезы о распределении генеральной совокупности по биномиальному закону
- •§4. Проверка гипотезы о равномерном распределении генеральной совокупности
- •§5. Проверка гипотезы о распределении генеральной совокупности по закону Пуассона
- •§6. Понятие о простейших случайных процессах
§4. Интервальные оценки
Интервальной называют оценку, которая определяется двумя числами − концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.
1. Интервальной
оценкой (с
надежностью
)
математического ожидания а
нормально распределенного количественного
признака X
по выборочной
средней
![]() при известном среднем квадратическом
отклонении
генеральной совокупности служит
доверительный интервал
при известном среднем квадратическом
отклонении
генеральной совокупности служит
доверительный интервал
![]()
где
![]() − точность оценки,n
− объем выборки,
t
− значение
аргумента функции Лапласа Ф(t),
при котором
− точность оценки,n
− объем выборки,
t
− значение
аргумента функции Лапласа Ф(t),
при котором
![]() ;
при неизвестном
(и объеме выборки n < 30)
;
при неизвестном
(и объеме выборки n < 30)
![]()
где s − «исправленное» выборочное среднее квадратическое отклонение, t находят по таблице по заданным n и .
2. Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного количественного признака X по «исправленному» выборочному среднему квадратическому отклонению s служит доверительный интервал
s(1 − q) < < (1 + q) (при q < 1),
0 < < s (1 + q) (при q > 1),
где q находят по таблице по заданным n и .
3. Интервальной оценкой (с надежностью ) неизвестной вероятности р биномиального распределения по относительной частоте w служит доверительный интервал (с приближенными концами p1 и p2)
p1 < p < p2,
где
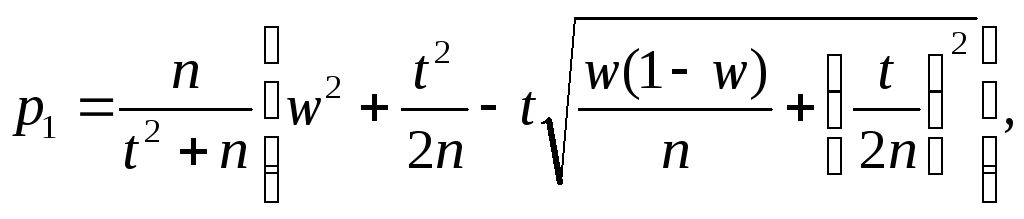
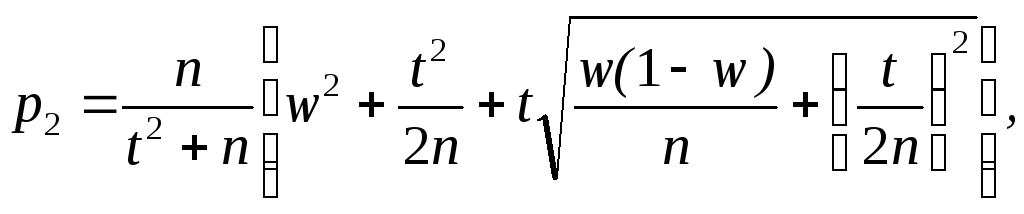
где
n
− общее
число испытаний; m
− число
появлений события; w
− относительная частота, равная отношению
![]() ;
t
− значение
аргумента функции Лапласа, при котором
;
t
− значение
аргумента функции Лапласа, при котором
![]() (
− заданная надежность).
(
− заданная надежность).
Замечание. При больших значениях n (порядка сотен) можно принять в качестве приближенных границ доверительного интервала
![]()
Тема 6. Оценка независимой вероятности событий по частоте
§1. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (например, А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону A.
Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины — критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Имеется несколько критериев согласия: 2 («хи квадрат») К. Пирсона, Колмогорова, Смирнова и др. Рассмотрим применение критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
A. Эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот. Пусть эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот:
![]()
Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность X распределена нормально.
Правило 1. Для того чтобы при заданном уровне значимости , проверить гипотезу о нормальном распределении генеральной совокупности, надо:
1. Вычислить
непосредственно (при малом числе
наблюдений) или упрощенным методом (при
большом числе наблюдений), например
методом произведений или сумм, выборочную
среднюю
![]() и выборочное среднее квадратическое
отклонениеB;
и выборочное среднее квадратическое
отклонениеB;
2. Вычислить теоретические частоты
![]()
где п − объем выборки (сумма всех частот), h − шаг (разность между двумя соседними вариантами),
![]()
![]()
3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
а) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия
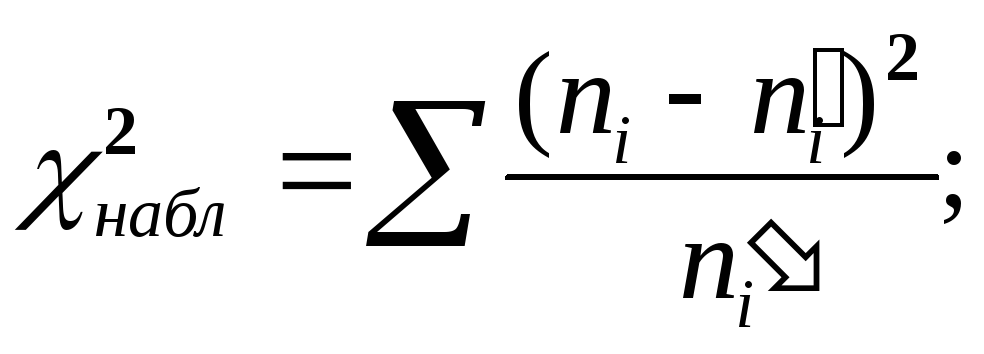
|
i |
ni |
|
ni
|
(ni
|
(ni
|
|
1 |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
|
9 |
… |
… |
… |
… |
… |
|
|
… |
… |
… |
… |
|
б) по
таблице критических точек распределения
2,
по заданному уровню значимости
и числу
степеней свободы k = s − 3
(s − число
групп выборки) находят критическую
точку
![]() правосторонней критической области.
правосторонней критической области.
Если
![]() − нет оснований
отвергнуть гипотезу о нормальном
распределении генеральной совокупности.
Другими словами, эмпирические и
теоретические частоты различаются
незначимо (случайно). Если
− нет оснований
отвергнуть гипотезу о нормальном
распределении генеральной совокупности.
Другими словами, эмпирические и
теоретические частоты различаются
незначимо (случайно). Если
![]() .− гипотезу
отвергают. Другими словами, эмпирические
и теоретические частоты различаются
значимо.
.− гипотезу
отвергают. Другими словами, эмпирические
и теоретические частоты различаются
значимо.
Замечание 1. Малочисленные частоты (ni < 5) следует объединить; в этом случае и соответствующие им теоретические частоты также надо сложить. Если производилось объединение частот, то при определении числа степеней свободы по формуле k = s − 3 следует в качестве s принять число групп выборки, оставшихся после объединения частот.
Б. Эмпирическое распределение задано в виде последовательности интервалов одинаковой длины и соответствующих им частот. Пусть эмпирическое распределение задано в виде последовательности интервалов (xi, xi+1) и соответствующих им частот ni (ni — сумма частот, которые попали в i-й интервал):
![]()
Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность X распределена нормально.
Правило 2. Для того чтобы при уровне значимости проверить гипотезу о нормальном распределении генеральной совокупности, надо:
1. Вычислить,
например методом произведений, выборочную
среднюю
![]() и выборочное среднее квадратическое
отклонениеB,
причем в качестве вариант
и выборочное среднее квадратическое
отклонениеB,
причем в качестве вариант
![]() принимают среднее арифметическое концов
интервала:
принимают среднее арифметическое концов
интервала:
![]() .
.
2. Пронормировать
X,
т. е. перейти к случайной величине
![]() ,
и вычислить концы интервалов:
,
и вычислить концы интервалов:![]() ,
,
![]() ,
причем
наименьшее значение Z,
т. е. z1,
полагают равным ,
а наибольшее,
т. е. zs+1,
полагают равным .
,
причем
наименьшее значение Z,
т. е. z1,
полагают равным ,
а наибольшее,
т. е. zs+1,
полагают равным .
3. Вычислить теоретические частоты
![]() ,
,
где п объем выборки (сумма всех частот); Рi = Ф(zi+1) Ф(zi) вероятности попадания X в интервалы (xi, xi+1); Ф(Z) функция Лапласа.
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
а) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия Пирсона
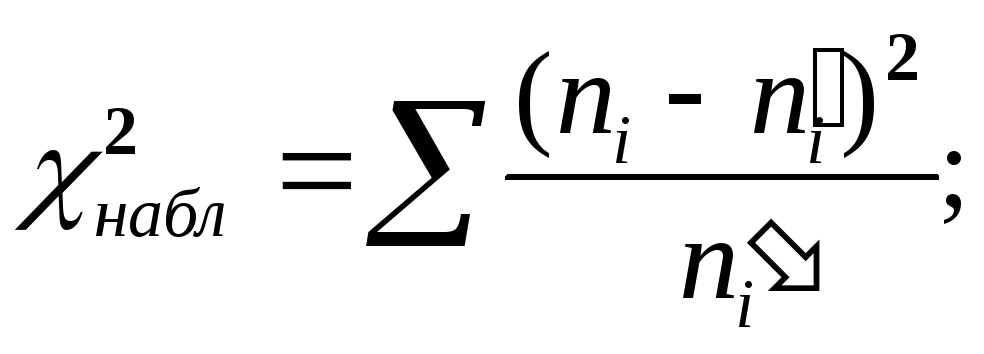
б) по
таблице критических точек распределения
2,
по заданному уровню значимости
и числу степеней свободы k = s 3
(s
число
интервалов выборки) находят критическую
точку правосторонней критической
области
![]() .
.
Если
![]()
нет оснований отвергнуть гипотезу о
нормальном распределении генеральной
совокупности. Если
нет оснований отвергнуть гипотезу о
нормальном распределении генеральной
совокупности. Если
![]() — гипотезу отвергают.
— гипотезу отвергают.
Замечание 2. Интервалы, содержащие малочисленные эмпирические частоты (пi < 5), следует объединить, а частоты этих интервалов сложить. Если производилось объединение интервалов, то при определении числа степеней свободы по формуле k = s 3 следует в качестве s принять число интервалов, оставшихся после объединения интервалов.
