§2. Иррациональные неравенства

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

M1_11_2012.pdf

Скачиваний:

115

Добавлен:

03.06.2015

Размер:

504.99 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы
			§2. Иррациональные неравенства
Иррациональными называют неравенства, в которых переменные
входят под знаком корня. Так как корень чётной степени существует
только у неотрицательных чисел, то при решении неравенств, содер-
жащих такое выражение, прежде всего удобно найти ОДЗ.
Пример 3. (МГУ, 1998) Решите неравенство									x +3 > x +1.
♦ Это			неравенство можно
решить	несколькими				способа-
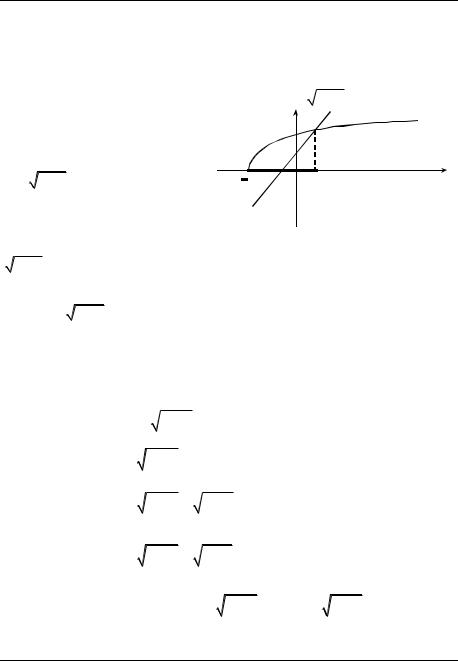
ми. Решим его графически (рис.
1). Построим графики функций											x
y = x +3 ,			y = x +1		и по-	3			1		x
смотрим, где первый график
расположен выше второго. Для
нахождения решения останется
решить		только		уравнение				Рис. 1
x +3 = x +1 (и не надо рассматривать случаи раз-
ных знаков для x +1!).
					x +1 ≥ 0,			x	=1 x [−3;1).
			x +3 = x +1					x	=1 x [−3;1).
		[			x +3 = x2 + 2x +1
Ответ:			−3;1 . ♦
			)
Сначала приведём уже выведенные в 10-ом классе условия равно-
сильности для уравнений (в частности, для того, чтобы была понятна
приведённая уже здесь нумерация условий равносильности для корней
(УР К)):					f (x) = a2 f (x)= a4 .						(УР К 1)
						g (x)≥ 0,
					f (x) = g (x)
					f (x) = g (x)	f	(x)= g 2		(x).		(УР К 2)

						ОДЗ	(x)= g (x).				(УР К 3)
					f (x) = g (x) f		(x)= g (x).				(УР К 3)
						f (x)= g (x),
								(x)≥ 0,			(УР К 4)
					f (x) = g (x) f			(x)≥ 0,			(УР К 4)
								(x)≥	0.
							g	(x)≥	0.

	п.1. Неравенства вида					f (x) ≥ g (x) и				f (x) ≤ g (x).
ОДЗ:	f (x)≥ 0 .
© 2012, ЗФТШ МФТИ. Колесникова София Ильинична											7
											7

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

Рассмотрим неравенство f (x) ≥ g (x). Докажем, что

		g			(x )< 0,

					(x )≥ 0;
			f		(x )≥ 0;
		f (x ) ≥ g (x )	g		(x )≥ 0,			(УР К5)

				f	(x )≥ g	2	(x ).
				f	(x )≥ g		(x ).

1. Если	x является решением				неравенства			f (x) ≥ g (x),	то
f (x)≥ 0 и	f (x) существует. При этом неравенство заведомо выпол-

нено при g (x)< 0. Если же g (x)≥ 0, то возведение в квадрат обеих

частей неравенства приводит к равносильному неравенству f 2 (x)≥ g 2 (x).

2. Пусть теперь x является решением совокупности неравенств

	g (x)< 0,


	f (x)≥ 0;

	g (x)≥ 0,

		f (x)≥ g		2	(x).
		f (x)≥ g			(x).
Тогда: а) если g (x)< 0 и						f (x) и заведо-
Тогда: а) если g (x)< 0 и	f (x)≥ 0,		то существует			f (x) и заведо-
мо выполнено неравенство	f (x) ≥ g (x);
б) если g (x)≥ 0 и f (x)− g 2(x)≥ 0 (			f (x)− g (x))(			f (x)+ g (x))≥ 0,
то f (x)− g 2 (x)≥ 0 f (x)− g (x)≥ 0.

Можно ОДЗ неравенства найти отдельно, тогда условие равносильности примет вид:

g (x)< 0;

ОДЗ

f (x) ≥ g (x) g (x)≥ 0, (УР К6)

f (x)≥ g 2 (x).

Теперь рассмотрим неравенство вида

f (x) ≤ g (x).

Докажем, что

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы
g (x)≥ 0,
	(x),		(УР К7)
f (x) ≤ g (x) f (x)≤ g 2
f (x)≥ 0.		f (x) ≤ g (x), то	f (x)≥ 0
1. Если x является решением неравенства

и существует			f (x),	а тогда	g (x)≥ 0,		и возведение в квадрат обеих
частей		неравенства		приводит		к	равносильному		неравенству
f	(x)≤ g 2	(x).
									g (x)≥ 0,
	2. Если x		является решением системы неравенств						f (x)≤ g 2 (x),
	f (x)≥ 0				f (x),				f (x)≥ 0,
то	f (x)≥ 0		и существует		f (x),		а тогда	f (x)− g 2 (x)≤ 0
( f (x)− g (x))( f (x)+ g (x))≤0.						Но, по условию, g (x)≥ 0, поэто-
му f (x)− g 2 (x)≤ 0 f (x)− g (x)≤ 0.
	Пример 4. (МФТИ, 1998) Решите неравенство 3							3x2 −8x −3 >1 −2x.
	♦ Первый способ
Воспользуемся (УР К6):

1 −2x < 0,

3x2 −8x −3 ≥ 0;

3 3x2 −8x −3 >1 −2x 1

−2x ≥ 0,

(3x2 −8x

−3)>(1 −2x)2

x > 0,5,

−1

−∞;

[3; +∞);

[3; +∞)

34 −30 2

≤ 0,5,

−∞;

34 −30 2

34 +30 2

−∞;

; +∞

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

		34 −30	2	[3; +∞).
x	−∞;
x	−∞;	23
		23

		34	−30	2	[3; +∞).
Ответ:	−∞;	34	−30	2
Ответ:	−∞;
			23
			23

Второй способ

Можно оформить решение неравенства и несколько по – другому. Найдём сначала ОДЗ:

	2		1					1	[3; +∞).
3x		−8x −3 ≥ 0 (x −3) x +		≥ 0	x		−∞; −
			3					3

Теперь неравенство перепишем в виде 3						3x2 −8x −3 −(1 −2x)> 0.

1.Если 1 −2x < 0 , т. е. x > 12 , то неравенство выполнено в ОДЗ, т. е.

x[3; +∞).

2.Если 1 −2x ≥ 0 , т. е. x ≤ 12 , то

3 3x2 −8x −3 >1 −2x 9(3x2 −8x −3)>1 −4x + 4x2

34 −30 2

+30 2

23x2 −68x −28 > 0 x

−∞;

; +∞ .

Заметим, что ОДЗ в этом случае выполнилось автоматически.

Учтём, что x ≤

− тогда x

34 −30

−∞;

Объединяя 1 и 2, получаем

34 −30

Ответ: −∞;

[3; +∞). ♦

f (x) ≤

g (x).

п.2. Неравенство вида

Рассмотрим неравенство вида

f (x) ≤

g (x).

Докажем, что

f (x)≤ g (x),

(УР К8)

f (x) ≤ g (x)

f (x)≥ 0.

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

1. Если	f (x) ≤ g (x), то		f (x)≥ 0,		g (x)≥ 0 и	f (x)≤ g (x),	т. е.
					f (x)≤ g (x),
x является решением системы неравенств
x является решением системы неравенств
					f (x)≥ 0.
						f (x)≤ g (x),
						f (x)≤ g (x),
2. Если	x является решением системы неравенств						то
2. Если	x является решением системы неравенств					f (x)≥ 0,	то
		f (x)
f (x)≥ 0,	g (x)≥ 0,	f (x)	и	g (x) существуют. При			этом
f (x)≤ g (x) f (x) ≤		g (x), т. е. неравенство выполнено.

Замечание. Для строгих неравенств в условиях равносильности надо простозаменитьзначок ≥ или ≤ на > или < соответственно.

Пример 5. Решите неравенство

2x +1 ≤ x3 −4x2 + x +5.

♦ 2x +1 ≤ x3 −4x2 + x +5

≤ x

−4x

+ x +5 x

−4x

− x + 4 ≥ 0,

2x +1

2x +1 ≥ 0.

(x −1)(x +1)(x −4)≥ 0 x [−1;1] [4;+∞),

[4;+∞).

x −

x ≥ −

Ответ:

−

;1 [4;+∞). ♦

п.3. Неравенствавида

f (x)− g(x)

≤0.

h(x)

Рольсопряжённыхвыражений

Обычно при решении неравенств, имеющих ОДЗ, надо сначала найт ОДЗ. При нахождении ОДЗ такого сложного неравенства, как

f (x)− g (x)		≥ 0,	учителя и школьники обычно решают систему

h(x)
f (x)≥ 0,
	Затем школьники иногда ошибочно опускают знаменатель
h (x)≠ 0 .	Затем школьники иногда ошибочно опускают знаменатель

и решают неравенство f (x)− g (x)≥ 0.

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

Мы в ОДЗ дроби не будем записывать условие h(x)≠ 0 и тем более

не будем тратить время и силы на решение этого неравенства. Оправдывается это тем, что в дальнейшем используем только классический метод интервалов для рациональных функций, в котором условие

h(x)≠ 0 автоматически выполняется, ибо нули знаменателя наносятся на числовую ось кружочками («дырками»), т. е. ограничение h (x)≠ 0 заложено в самом методе. Это ОДЗ, которое отличается от привычного школьного (c h (x)≠ 0), по предложению самих учителей, будем обозначать не ОДЗ, а ОДЗ*. Итак, например, для неравенств вида

f (x ) − g (x )

( ) ≥ 0 будем искать ОДЗ*: f (x)≥ 0 . h x

Рассмотрим довольно часто встречающееся неравенство вида

f (x)− g (x)	≥ 0 (≤ 0).
h (x)

Вметодической литературе предлагается рассмотреть две системы

взависимости от знака знаменателя h (x), причём в каждой есть не-

равенство с корнем. Энтузиазм решать задачу при этом быстро «испаряется».

Мы поступим иначе: рассмотрим два случая в зависимости не от знака h (x), а от знака g (x), и неравенств с корнем решать не придёт-

ся.

Рассмотрим отдельно разность f (x)− g (x). Отметим две особенности поведения этой разности:

1)если g (x)< 0, то разность f (x)− g (x) положительна в ОДЗ;

2)если g (x)≥ 0, то разность f (x)− g (x) может быть как положи-

тельной, так и отрицательной в ОДЗ. Заметим, однако, что в этом случае сумма f (x)+ g (x) всегда неотрицательна в ОДЗ, а умножение разности

( f (x)− g (x))на неотрицательное выражение( f (x)+ g (x))не изменит
знакаразности, т. е. выражение
(	f (x)−g (x))( f (x)+ g (x))≡ f (x)−g2 (x)

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

имеет тот же знак, что и ( f (x)− g (x)) в ОДЗ. Новое выражение уже не содержит радикалов (корней), а выражение ( f (x)+ g (x)) называется сопряжённым для ( f (x)− g (x)) выражением. Отсюда следует важное правило ПК1:

Если g (x)≥ 0 , то знак разности	f (x)− g (x) совпа-	(П К1)
дает со знаком разности f (x)− g 2 (x)	в ОДЗ.

Теперь используем эти свойства для решения довольно сложных неравенств вида

f (x)− g (x)	≥ 0 или	( f (x)− g (x))h(x)≥ 0.
h (x)

Сейчас мы покажем, что можно обойтись, хотя и двумя случаями, но без корней.

f (x)− g (x)

Рассмотрим, для определённости, неравенство ( ) ≥ 0. h x

1. Мы уже заметили, что, если g (x)< 0, то числитель положителен

		f (x)− g (x)	ОДЗ
в ОДЗ. Но тогда			≥ 0 h(x)> 0.
		h(x)
2. Если же	g (x)≥ 0, то разность может менять знак в зависимости
от значений x,	но сумма f (x)+ g (x) всегда неотрицательна в ОДЗ, и

умножение обеих частей неравенства на это сопряжённое выражение

приводит к		равносильному неравенству, т. е. в			этом	случае
	f (x)− g (x)	ОДЗ	f (x)− g 2 (x)
		≥ 0		≥ 0. Для неравенства	другого	знака
	h(x)	≥ 0	h (x)	≥ 0. Для неравенства	другого	знака

меняется лишь знак неравенства. Объединив оба условия, получаем новое замечательное условие равносильности в ОДЗ:

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

g (x )< 0,

f (x ) − g (x ) ≥ 0 (≤ 0 )

h (x )> 0 (< 0 ),

(УРК16)

g (x )≥ 0,

ОДЗ

h (x )

(x )

f (x )− g

≥ 0

(≤ 0 ).

h (x )

Найденные в результате исследования совокупности (УР К9) реше-

ния следует сравнить с ОДЗ.

4x +15 −4x2

Пример 6. (МГУ, 1995) Решите неравенство

≥ 0.

4x +15

+ 2x

♦ ОДЗ*. 4x +15 ≥ 0 x ≥ −					15		. Теперь в ОДЗ преобразуем неравен-
						4
ство:	4x	+15 −4x2		( 4x +15 +			2x)( 4x +15 −2x)	≥ 0
			=			4x +15 + 2x

	4x +15 + 2x

	4x +15	−2x ≥ 0,

	4x +15	+ 2x ≠ 0.

Попробуем решить эту систему графически. Из графика на рис. 2 видно, что неравенство выполнено от

точки x = −154 до абсциссы точки

пересечения кривой y = 4x +15 и прямой y = 2x .

Найдём эту абсциссу:

15	3	5	x
4	2	2

Рис. 2

			2x ≥ 0,
					3
2x ≥ 0,					3			5
4x +15 = 2x		2	x	= −		2	, x =	5	.
4x +15 = 2x		2	x			2	, x =		.
4x +15 = 4x					5		2
					5
			x	=
			x	=	2
Заметим, что для решения					2
Заметим, что для решения	уравнения мы возводили обе части в квад-
рат, а, значит, одновременно с нашим решили «чужое» уравнение:
							2x ≤ 0,
4x +15 +2x = 0 4x +15 = −2x										= 4x2 .
							4x +15			= 4x2 .

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

А в нашей системе решение этого уравнения x = −32 как раз нам надо

исключить. Главное в том, что для решения всей системы оказалось достаточно решить единственное уравнение

																																3
																											x = −						,
												4x +15 = 4x										2					x = −					2	,
																						2								5		2


																											x =					.
																											x =			2		.
																														2
														Ответ: x												15				3						3			5
Теперь можно записать																								−					; −				−				;			. ♦
Теперь можно записать																								−		4			; −	2			−			2	;		2	. ♦
																										4				2						2			2
Пример 7. Решите неравенство																									2 − x + 4x −3										≥ 2 .
Пример 7. Решите неравенство																																			≥ 2 .
► Найдём сначала ОДЗ*:																													x					Теперь воспользуемся
► Найдём сначала ОДЗ*:																		2 − x ≥ 0 x ≤ 2.																Теперь воспользуемся
(УР К9):															2 − x +(2x									−3)										2 − x −(3								−2x)
	2 − x				+ 4x −3										2 − x +(2x									−3)										2 − x −(3								−2x)			Î ÄÇ*
								≥	2																			≥ 0																≥ 0
					x			≥	2										x									≥ 0											x					≥ 0
					x														x																				x
																																								3
			3 − 2x < 0,																			3														x >						,
			3 − 2x < 0,																			3														x >						,
					> 0;													x >				2		,																2	3
			x		> 0;																	2	3															x ≤			3		,
		3 − 2x ≥ 0,

																		x			≤				,																2
																		x			≤		2		,																2
																						2	2																				7
											2											2																					7
				2 − x −(2x −3)							2									4x −11x + 7																		x − 4 (x −1)
				2 − x −(2x −3)									≥ 0																		≤ 0


							x																		x																					≤ 0
							x																																							≤ 0
																																											x
																																											x
						3
		x >					,								ñ ó÷¸ ò î ì Î ÄÇ*
		x >				2	,								ñ ó÷¸ ò î ì Î ÄÇ*
						2																		x (−∞;0) [1; 2].
												3
			x (−∞; 0)									3
									1;
									1;
												2
												2
															3
									x ≤							,
									x ≤						2	,
Систему неравенств															2													решили классическим методом
																7
																7
										x				−		4	(x −1)
																4							≤ 0
																	x						≤ 0
интервалов – рис. 3.																	x

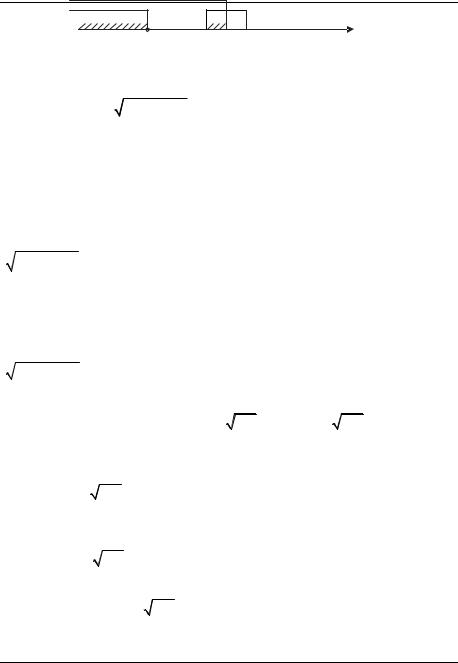
2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

•

•	•	•
1	1,5 1,75		х

Ответ: (−∞; 0) [1; 2]. ◄				Рис. 3

Пример 8.	x2	−4x +3 −2		(x +7)	≤ 0.
		x2	− x −72

► Неравенство довольно громоздкое и сложное.
Найдём сначала			ОДЗ*:	x2 −4x +3 ≥ 0 (x −1)(x −3)≥ 0

x (−∞; 1] [3; +∞). Затем рассмотрим отдельно два случая в зави-

симости от знака (x +7).
	1. Если x +7 < 0 x < −7, то числитель положителен					в ОДЗ* и
	x2 −4x +3 −2(x +7)			ОДЗ*	(x +8)(x −9)< 0
			≤ 0	x2 − x −72 < 0
	x2	− x −72

	x (−8;	−7). Учитывая ограничение x < −7,			получаем, что	Оказалось,

что этот промежуток принадлежит ОДЗ*.

2. Если x +7 ≥ 0 x ≥ −7, то воспользуемся правилом П К1. Тогда

x2 −4x +3 −2(x +7)

≤ 0

ОДЗ* (x2 −4x +3)−(2(x +7))2

≤ 0

x2 − x −72

(x −9)(x +8)

−30 − 321

−30 +

321

x −

+60x

+193 ≥ 0

≥ 0

(x +8)(x −9)

x≥−7

(x +8)(x −9)

−30 +

321

(9;

+∞) с

учётом ограничения x ≥ −7. Оказа-

−7;

лось, что и эти промежутки принадлежат ОДЗ*. Поэтому

−30 +

321

(9;

+∞).

x −8;

−30 +

321

(9;

+∞). ◄

Ответ:

−8;

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

	п.4. Неравенства вида	f (x )−		g (x )	≥ 0 (≤ 0).
		h(x )

Роль сопряжённых выражений
Теперь рассмотрим неравенство вида			f (x)−		g (x)	≥0 (≤0).

				h(x)
На вид довольно сложное неравенство. Разность				f (x)−		g (x) где-то на
числовой	оси положительна, где-то	отрицательна,			но	сумма корней
f (x)+	g (x) всегда неотрицательна в ОДЗ. Поэтому умножение обеих

частей неравенства на это сопряжённое выражение приводит к равносильномувОДЗнеравенству, и имеетместоусловиеравносильностивОДЗ

f (x)−	g (x)	≥ 0	ОДЗ	f (x)− g (x)	≥ 0 (УРК10),
h(x)				h(x)

или полное условие равносильности, включающее ОДЗ:


	f (x)−	g (x)	f (x)≥ 0,
	f (x)−	g (x)					(УР К11)
			≥ 0 g (x)≥ 0,
	h (x)		≥ 0 g (x)≥ 0,
	h (x)		f (x)− g		(x)
			f (x)− g		(x)	≥ 0
				h (x)		≥ 0
Отсюда, в частности, следует полезное правило (П К2):
Знак разности			f (x) −	g (x) совпадает со знаком разности
f (x)− g (x)		в ОДЗ.					(П К2)

Пример 9. (Демоверсия ЕГЭ - 2010) Решите неравенство

1− x3 −1 ≤ x. x +1

и найдите наименьшую длину промежутка, который содержит все его

решения.

►Замечательный пример на применение (УР К11)!

Приведём всё к общему знаменателю, затем разложим разность кубов на множители. При этом учтём, что неполный квадрат суммы

x2 + x +1никогда в 0 не обращается – он всегда положителен, потому

2012-2013 уч. год, № 1, 11 кл. Математика. Алгебраические уравнения, неравенства, системы

что его дискриминант отрицателен. Поэтому на x2 + x +1 можно со-

кратить. Затем воспользуемся (УР К11), или, что то же, тем, что умножение неравенства на положительное сопряжённое выражение приводит к равносильному неравенству. Тогда

(

1 − x3 −1

≤ x

1 − x3

−1 − x − x2

≤ 0

1 + x

(1 − x)(x2 + x +1)−( x2 + x +1)2

≤ 0

1 − x − x2 + x +1

≤ 0

1 + x

1−x − x2 +x +1)( 1−x + x2 +x +1)

1−x ≥0,

(

x2 +x +1

1+x

≤0 (1−x)−

)

≤0

1+x

x ≤1,
						x [−2;	−1) [0; 1].
x (x + 2)	≥ 0 x	−2; −1		0; + ∞	)

	[	)	[
1 + x

Неравенство решено методом интервалов – рис. 4.

Наименьшая длина промежутка, который содержит все решения, равна 3.

Рис. 4
Ответ: [−2; −1) [0; 1], 3. ◄
Пример 10. Решите неравенство	4x2	−3x + 2 −		4x −3	≤ 0	и най-
Пример 10. Решите неравенство		x2 −5x +	6		≤ 0	и най-
		x2 −5x +	6

дите наименьшую длину промежутка, который содержит все его решения.

► Найдём сначала ОДЗ*:

−3x + 2 ≥ 0, x ≥

4x −3 ≥ 0

Теперьможнорешитьнеравенство, применивправило(ПК2) :

4x2 −3x +2 −

4x −3

ОДЗ* 4x2

−3x +2 −4x +3

≤ 0

≤

x2 −5x +

x2 −5x +6

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.06.2015319.88 Кб4Lektsii_zubova_2.pdf
#
03.06.2015450.28 Кб5Leonidov.pdf
#
03.06.2015550.54 Кб3LM1117.pdf
#
03.06.201520.96 Mб96M.A.Leontovich-термодинамика и стат физика.pdf
#
03.06.2015688.23 Кб77M1_10_14.pdf
#
03.06.2015504.99 Кб115M1_11_2012.pdf
#
03.06.2015581.89 Кб44M1_8_14.pdf
#
03.06.2015849.06 Кб70M3_10_14.pdf
#
03.06.2015603.08 Кб48M3_8_14.pdf
#
03.06.2015364.31 Кб61M3_8_2010.pdf
#
03.06.2015654.44 Кб53M4_10_14.pdf