
- •РАБОЧАЯ ТЕТРАДЬ ПО ТЕМАМ 6.1, 6.2
- •Тема 6.1. Интегрирование функций нескольких переменных
- •Двойной интеграл
- •Задача 1.1
- •Задача 1.2
- •Справочный материал
- •Решение задачи 1.1
- •Решение задачи 1.2
- •Задача 2.1
- •Задача 2.2
- •Справочный материал
- •Механический смысл двойного интеграла
- •Геометрический смысл двойного интеграла
- •Решение задачи 2.1
- •Решение задачи 2.2
- •Тройной интеграл
- •Задача 3.1
- •Задача 3.2
- •Задача 3.3
- •Справочный материал
- •Решение задачи 3.1
- •Решение задачи 3.2
- •Тройной интеграл в сферических координатах
- •Решение задачи 3.3
- •Задача 4.1
- •Задача 4.2
- •Задача 4.3
- •Справочный материал
- •Решение задачи 4.1
- •Решение задачи 4.2
- •Решение задачи 4.3.
- •Задача 5.1
- •Задача 5.2
- •Задача 5.3
- •Справочный материал
- •Решение задачи 5.1
- •Решение задачи 5.2
- •Решение задачи 5.3
- •Задача 6.1
- •Задача 6.2
- •Задача 6.3
- •Справочный материал
- •Решение задачи 6.1
- •Решение задачи 6.2
- •Решение задачи 6.3
- •Тема 6.2. Теория поля
- •Скалярное поле
- •Задача 7.1
- •Задача 7.2
- •Задача 7.3
- •Справочный материал
- •Решение задачи 7.1
- •Решение задачи 7.2
- •Решение задачи 7.3
- •Векторное поле
- •Задача 8.1
- •Задача 8.2
- •Справочный материал
- •Решение задачи 8.1
- •Решение задачи 8.2
- •Задача 9.1
- •Задача 9.2
- •Справочный материал
- •Решение задачи 9.1
- •Решение задачи 9.2
- •Задача 10
- •Справочный материал
- •Теорема Стокса
- •Решение задачи 10
- •Задача 11
- •Справочный материал
- •Решение задачи 11
- •Задания к типовым расчетам
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •ПРИЛОЖЕНИЕ
- •Полярная система координат
- •Эллиптические координаты
- •Сферическая система координат
- •Обобщенно эллиптические координаты
- •Механические приложения интегралов функций нескольких переменных
- •Механические приложения двойных интегралов
- •Статические моменты
- •Координаты центра тяжести
- •Моменты инерции
- •Механические приложения тройного интеграла
- •Статические моменты
- •Координаты центра тяжести
- •Моменты инерции
- •Механические приложения криволинейного интеграла первого рода
- •Статические моменты дуги
- •Координаты центра тяжести дуги
- •Моменты инерции дуги
- •Механические приложения поверхностного интеграла первого рода
- •Статические моменты участка поверхности
- •Моменты инерции участка поверхности
|
|
|
b |
g2 |
(y) |
(x, y)dx , если область интегрирования |
||||
2. ∫∫ f (x, y)dS = ∫dy |
∫ f |
|||||||||
D |
|
|
a |
g1 |
(y) |
|
|
|
|
|
можно представить в виде |
|
a ≤ y ≤ b |
|
. |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
g1 (y)≤ x ≤ g2 (y) |
|
|
|||
ЗАМЕЧАНИЕ 1 |
|
|
|
|
|
|
|
|
||
Если |
границы |
области |
D , |
по которой |
вычисляется |
двойной |
||||
интеграл, можно задать только различными уравнениями, то |
||||||||||
область интегрирования D разбивается на две или более частей. |
||||||||||
ЗАМЕЧАНИЕ 2 |
|
|
|
|
|
|
|
|
||
Вычислять |
повторный |
интеграл, |
например |
интеграл |
||||||
b |
g2 (x) |
|
|
|
|
|
|
|
|
|
∫dx |
∫ f (x, y)dy , следует, |
начиная с частного интегрирования |
||||||||
a |
g1(x) |
|
|
|
|
g 2 (x) |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
по |
внутреннего интеграла |
∫ f (x, y)dy . После подстановки |
||||||||
|
|
|
|
|
|
|
g1 (x) |
|
|
x . Ее |
пределов интеграции получится функция переменной |
||||||||||
нужно проинтегрировать по переменной x в пределах от a до b .
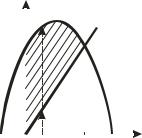
Решение задачи 1.1
Прежде всего восстановим по пределам интегрирования вид
области D , по которой |
берется |
двойной |
интеграл. |
Область D |
|||||||||||||||||||||
находится в полосе между прямыми |
х = 0 |
и х = 2 |
и ограничена |
||||||||||||||||||||||
снизу линией у = |
3х |
, а сверху линией у = 4 − (х −1)2 (рис.1). |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||
2 |
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у=4-( х-1)2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
3х |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
у |
|
= |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
|
1 |
|
|
2 |
3 |
х |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. |
|
|
|
|
|||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||
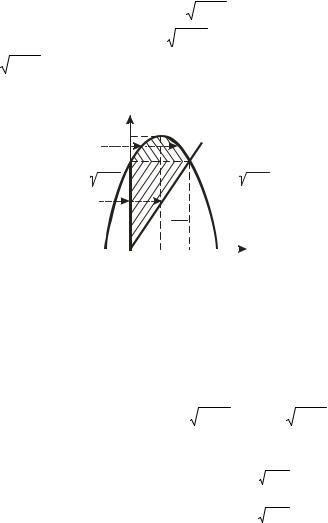
Если область D спроектировать на ось Оу , то она попадет в полосу между прямыми у = 0 и у = 4 . Чтобы найти левую и правую
границы области |
D , решим уравнение параболы |
у = 4 − (х −1)2 |
|||||||
относительно х. |
Получим |
х =1 ± 4 − у , причем линия АВ |
|||||||
определяется уравнением х =1 − |
4 − у , |
а линия ВС уравнением |
|||||||
х =1 + 4 − у . |
Уравнение |
прямой |
у = |
3х |
|
также решим |
|||
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
относительно х и запишем в виде: |
х = |
2 у |
. |
|
|
|
|
||
|
|
|
|
|
|||||
|
|
|
3 |
|
|
|
|
|
|
у |
В |
|
|
4 |
|
||
D2 |
|
||
А |
С |
||
х=1- 4-у3 |
D1 |
||
х=1+ 4-у |
х=23у
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
|
|
1 |
2 |
3 |
х |
||||
|
|
|
|
|
|
|
|
|
Рис. 2. |
|
|
|
||
Из рисунка 2 видно, что левая и правая граница области |
||||||||||||||
интегрирования |
D состоит из двух линий. |
Следовательно, область |
||||||||||||
D следует разбить на две части |
D1 и |
D2 . Эти области задаются |
||||||||||||
неравенствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D : |
0 ≤ у ≤ 3 |
D |
|
: |
3 ≤ у ≤ 4 |
|
|
|||||||
|
|
2 у |
|
2 |
|
|
|
|
|
|||||
1 |
0 ≤ х≤ |
, |
|
|
|
1 − 4 − у ≤ х≤1 + 4 − у. |
||||||||
|
|
|
|
|
|
|||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда заданный повторный интеграл будет представлен суммой двух интегралов.
2 |
4−(х−1)2 |
3 |
2 |
у |
4 |
1+ |
4− у |
|||
3 |
||||||||||
∫dx |
|
∫ f |
(x, y)dy = ∫dу ∫ f (x, y)dх+ ∫dу |
|
∫ f (x, y)dx . |
|||||
0 |
|
3 |
x |
|
0 |
0 |
3 |
1− |
4− у |
|
|
2 |
|
||||||||
5
Решение задачи 1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прежде чем расставлять пределы интеграции в другом порядке, |
||||||||||||||||||
выясним, по какой области ведется интегрирование в каждом |
||||||||||||||||||
интеграле. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая пределы интеграции, можно выписать следующие |
||||||||||||||||||
неравенства для областей D1 и D2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
− 2 2 ≤ y ≤ −2 |
|
|
|
|
|
− 2 ≤ y ≤ 2 |
|
|
|
|
|||||||
|
|
(D1 ) и |
|
|
|
|
|
|
|
|
|
|
|
(D2 ). |
||||
|
− y2 ≤ x ≤ 8 − y2 |
|
|
≤ x ≤ |
|
8 − y2 |
|
|
||||||||||
− 8 |
|
|
y |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, область D1 ограничена кривыми: |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
y = −2 |
|
|
|
|
|
|
|
||||
|
y = −2 2, y = −2 |
|
|
, |
|
|
|
|
||||||||||
|
|
= ± |
8 − y2 |
или |
|
|
|
|
|
8 |
|
|
|
|
||||
|
x |
|
x2 + y2 = |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
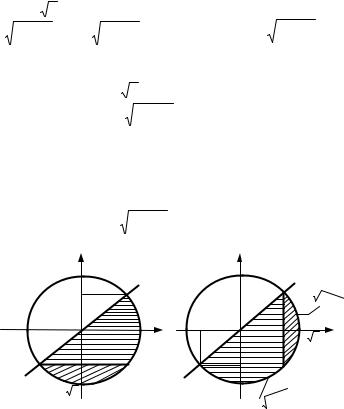
а область D2 ограничена кривыми (рис.3. а): |
|
|
|
|
|
|
|
|
|
|
||||||||
|
y |
= −2, y = 2 |
|
y = −2 |
|
|
|
|
|
|
|
|
||||||
|
|
x |
= y |
|
или |
|
|
x = y |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
+ y |
2 |
= 8 |
|
|
|
|
|
|
||
|
x = 8 − y2 |
|
x |
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
x |
|
|
|
|
y = |
8 |
− |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
y |
|
|
2 D2 |
|
|
|
|
|
||
|
|
D2 |
|
|
−2 |
|
|
|
|
|
|
|
x |
|
||||
|
|
|
x |
|
|
|
D1 |
|
|
|
|
2 |
2 |
|
|
|||
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
||
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
−2 2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3. а |
|
|
|
|
|
|
Рис.3. б |
|
|
|
|
|
|
||||
Если поменять порядок интегрирования, то область придется |
||||||||||||||||||
разбить на две области прямой |
x = 2 |
(рис. 3. б). Тогда области |
||||||||||||||||
интегрирования D1 и D2 можно задать неравенствами: |
|
|
|
|
|
|||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
