
Матеша 3 семак.docx
.pdf
СЕМЕСТР 3. ВОПРОСЫ К ЭКЗАМЕНУ
1. Определение и свойства двойного интеграла.
Интегральной суммой для функции f(x,y) по области D называется сумма вида:
∑ ( , )∆ = ( 1, 1)∆1 + … + ( , )∆
=1
Если предел |
|
|
, |
|
∆ |
|
|
существует и не зависит ни от способа разбиения области D на части, |
||||||||||||||
ни от выбора |
∑ |
|
|
|
|
|
(или |
|
|
), т.е |
|
|
|
|
||||||||
обозначается=1 ( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
точек в них, то он называется двойным интегралом от функции f(x,y) по области D и |
|||||||||||||||||||
|
|
|
( , ) |
|
|
|
( , ) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
, |
|
|
∆ |
, где |
( , ) |
— интегрируемая по области D функция, D — |
|||||||||
|
( , ) = ∑ |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
=1 |
|
|
и |
— переменные интегрирования, |
|
(или |
|
) — элемент площади. |
||||||||||
область интегрирования, |
||||||||||||||||||||||
Свойства двойного интеграла( ) |
: |
|
|
|
|
|
|
|
|
|||||||||||||
1.∙ ( , ) = ∙ ( , ) , — const
2.(1( , ) ± 2( , )) = 1( , ) ± 2( , )
3.Если область D разбить на две области 1 и 2 такие, что 1 ∩ 2 = , а пересечение 1 и2 состоит лишь из одной линии, их разделяющей, то
( , ) = 1( , ) + 2( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4. |
Если в области |
|
имеет место неравенство |
( , )≥0 |
, |
то и |
( , )≥0 |
. Если в |
|||||||||||||||||||||||||||||
области |
|
|
функции |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
, |
то |
и |
|||||||||||||||
|
|
|
|
|
|
|
( , ) |
|
|
|
φ( , ) |
удовлетворяют |
неравенству |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , )≥φ( , ) |
|
|
|
|||||||||||||||
( , ) ≥ φ( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5. |
|
|
= |
, тк |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∑ ∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
Если |
функция |
|
( , ) |
|
непрерывна |
в замкнутой |
области |
|
|
, |
площадь которой |
|
, |
то |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
— наименьшее и наибольшее |
|
|
|
|
|
|
|
|
|||||||||||||||
≤ ( , )≤ |
, |
где |
|
|
|
|
|
|
|
|
|
|
|
|
значения подынтегральной |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
функции в области |
|
|
|
|
|
|
|
|
непрерывна в замкнутой области |
|
, |
площадь которой |
|
, то в этой |
|||||||||||||||||||||||
7. |
Если |
функция |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)∙ |
|
|
|
|
|
|
|
|
|||||
области существует |
такая точка |
|
|
|
, что |
|
|
|
|
|
. Величину |
|
|
|
|
|
|||||||||||||||||||||
|
|
( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|
( , ) = ( , |
|
|
|
|
|
|
|
|
||||||||||
( , )= |
|
|
|
|
|
|
|
|
|
|
|
называют0 0 |
средним значение функции0 |
0 |
|
|
|
в области . |
|
|
|
|
|||||||||||||||
|
( , ) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|
|
|
|
|
|
|
|||||||||||||||||
2. Вычисление двойного интеграла в декартовой системе координат путем сведения к повторному. Пределы интегрирования (два случая).
Примеры.
Различают два основных вида области интегрирования (правильные):
1. Область интегрирования ограничена слева и справа прямыми = и = ( < ), а снизу и сверху — непрерывными кривыми = φ1( ) и = φ2( ) (φ1( )≤φ2( )), каждая из
которых пересекается вертикальной прямой только в одной точке
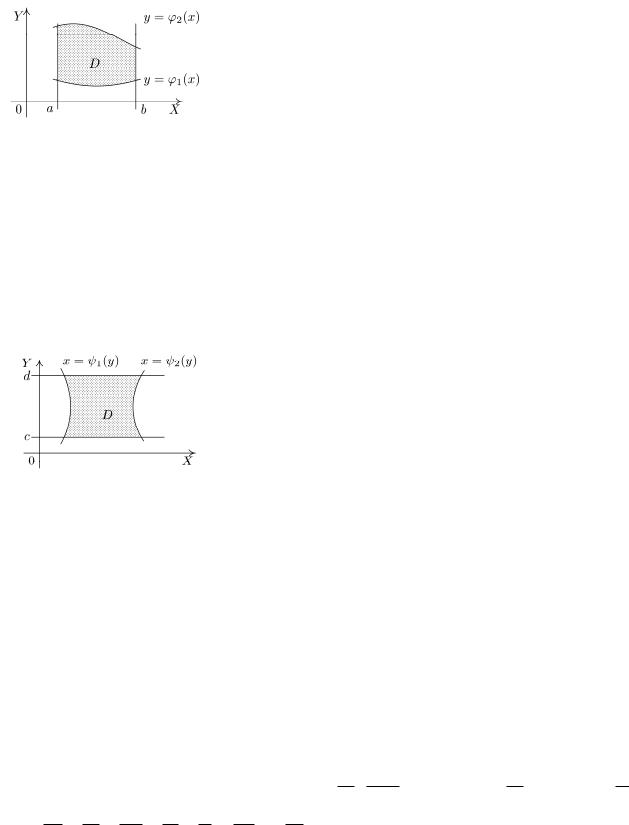
φ2( )
∫( ∫ ( , ) ) В этом выражении сначала вычисляется интеграл скобках, причём
φ1( )
интегрирование производится по переменной , а — постоянная. В результате интегрирования
получается непрерывная функция от : Ф( ) = |
φ2( ) |
|||||||
∫ ( , ) . Эту функцию интегрируем по в |
||||||||
пределах от |
|
до |
|
: |
|
|
. |
φ1( ) |
|
|
|
= ∫ Ф( ) |
|
|
|||
|
|
|
|
|
|
|
|
|
2. Область интегрирования ограничена снизу и сверху прямыми = и = ( < ), а слева и справа — непрерывными кривыми = ψ1( ) и = ψ2( ) (ψ1( )≤ψ2( )), каждая из
которых пересекается горизонтальной прямой только в одной точке
ψ2( )
∫( ∫ ( , ) ) В этом выражении сначала вычисляется интеграл скобках, причём
ψ1( )
интегрирование производится по переменной , а — постоянная.
Следовательно, двойной интеграл от непрерывной функции ( , ) по правильной области равен повторному интегралу от этой функции по области , те
|
|
|
|
|
ψ2( ) |
|
|
|
|
|
|
|
|
|
|
φ2( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( , ) σ = ∫( ∫ |
( , ) ) = ∫( ∫ |
( , ) ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
ψ1( ) |
|
|
|
|
|
|
|
|
|
|
φ1( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
Примеры №1. Вычислить |
|
( − ) |
, |
если область |
|
ограничена линиями |
= 2 |
− |
и |
|||||||||||||||||||||||||||||||
= 2 − 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение: Построим |
область |
|
. Первая линия — парабола |
с |
вершиной |
|
в точке (0,2), |
|||||||||||||||||||||||||||||||||
симметричная |
относительно |
|
|
|
. Вторая линия — прямая. Решая совместно уравнения |
|||||||||||||||||||||||||||||||||||
= 2 − |
2 |
и |
= 2 − 1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
найдем координаты точек пересечения: А(-3,-7), В(1,1). Область |
|||||||||||||||||||||||||||||||||||||
интегрирования принадлежит к первому виду. Находим: |
2− 2 |
|
|
1 |
|
3 |
|
4 |
|
|
|
2 |
|
|
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
2− 2 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
( − ) = ∫ |
∫ ( − ) = ∫ ( − |
2 |
)| |
2 −1 |
= |
∫ (− |
|
− |
2 |
+ + |
2 |
|
− |
2 |
) |
|||||||||||||||||||||||||
5 |
|
|
4 |
|
−3 |
|
2 −1 |
|
|
|
|
|
−3 |
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= (− |
10 |
− |
4 |
+ |
23 |
|
+ |
2 |
|
− |
23 |
)| |
−31 |
= 4 |
154 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

3. Замена переменной в двойном интеграле (общий случай). Определитель Якоби. Примеры.
Если функции = φ( , ) и = ψ( , ) имеют в некоторой области * плоскости непрерывные частные производные первого порядка и отличный от 0 определитель
( , ) = | |
∂ |
|
∂ |
|
∂ |
|
∂ |
| |
— определитель Якоби или якобиан, а функция |
( , ) |
непрерывна в |
|
|
∂ |
|
∂ |
|
∂ |
|
|
|||
| ∂ |
|
|
|
| |
|
|
|
||||
области , то справедлива формула замены переменной в двойном интеграле:
( , ) = *(φ( , ), ψ( , )) • |( , )|
4. Двойной интеграл в полярной системе координат. Вычисление якобиана. Пределы интегрирования (два случая). Примеры.
Пусть область интегрирования в полярных координатах определяется следующим образом: 0≤ (θ)≤ ≤ (θ), α≤φ≤β, где β − α≤2π. Тогда двойной интеграл в полярных координатах
описывается формулой: |
|
|
|
β (θ) |
|
|
|
|
Полярным |
|
|
( , )σ = ∫( ∫ ( φ, φ)φ |
|
|
|||
0≤ ≤ ≤, |
|
|
|
α (θ) |
|
|
|
|
|
|
|
|
|
|
|
||
прямоугольником называется область интегрирования, удовлетворяющая условиям: |
||||||||
α≤φ≤β, |
|
где |
β − α≤2π |
и |
описывается |
формулой: |
||
β
( , )σ = ∫(∫ ( φ, φ)φ
α
5.Приложения двойного интеграла.
●Площадь плоской фигуры = = φ
●Объем тела = ( , )
● Площадь |
|
|
|
|
|
|
|
|
|
|
|
|
поверхности |
|||||
= |
1 + ( |
∂∂ |
)2 |
+ ( |
∂∂ |
)2 = |
1 + ( |
∂∂ |
)2 |
+ ( |
∂∂ |
)2 = |
1 + ( |
∂∂ |
)2 |
+ ( |
∂∂ |
)2 |
●Масса плоской фигуры = γ( , )
● Статические моменты и координаты центра тяжести плоской фигуры = ∙γ( , ) и
; |
= |
|
и |
= |
|
= ∙γ( , ) |
|
|
|||

●Момент инерции плоской фигуры — произведение массы на квадрат расстояния точки до оси,
те = 2∙γ( , ) и = 2∙γ( , )
6. Определение и свойства тройного интеграла.
Если предел интегральной суммы существует при неограниченном увеличении числа таким образом, что каждая «элементарная область» стягивается в точку, то его называют тройным
интегралом от функции = ( , , ) по области и обозначают
|
|
|
|
|
|
|
, |
, |
)∆ |
|
= ( , , ) |
|
|
|||||
( , , ) = ∑ ( |
|
|
|
|||||||||||||||
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
— элемент объема. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема о существовании: Если функция |
при |
|
и |
|
непрерывна в ограниченной замкнутой |
|||||||||||||
области |
, то предел интегральной суммы |
= ( , , ) |
|
|
|
|||||||||||||
способа |
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
→0 |
|
в них. |
||
|
|
разбиения области |
|
на части, ни от выбора точек |
( , , ) |
|||||||||||||
Свойства: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. |
∙ ( , , ) = ∙ ( , , ) |
|
|
|
|
|
|
|||||||||||
2.(1( , , ) ± 2( , , )) = 1( , , ) ± 2( , , )
3.( , , ) = 1( , , ) + 2( , , )
4. |
|
( , , )≥0, |
если |
( , , )≥0; |
если |
( , , )≥φ( , , ), |
то |
( , , ) ≥ φ( , , ) |
|
|
|
|
|||
5. |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
6. Оценка интеграла ≤ ( , , )≤
7.Теорема о среднем значении: если функция ( , , ) непрерывна в замкнутой области, то в
этой области существует такая точка ( , , ), что ( , , ) = ( , , )∙
0 0 0 0 0
0 0
7. Вычисление тройного интеграла в декартовой системе координат путем сведения к повторному.
φ2( ) 2( , )
( , , ) = ∫ |
∫ |
∫ ( , , ) |
|
φ1( ) |
1( , ) |

8. Замена переменной в тройном интеграле (общий случай). Определитель Якоби.
Если функции |
( , , ), ( , , ), ( , , ) |
|
имеют в |
некоторой области |
|
* плоскости |
|
|||||||||||
непрерывные |
|
|
|
|
|
|
|
|||||||||||
|
|
частные производные первого порядка и отличный от 0 определитель |
|
|||||||||||||||
( , , ) = | |
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
|
|≠0 |
— |
определитель |
Якоби |
или якобиан, а |
|||
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
∂ |
∂, |
|
|
|
|
|
|
|
|||
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
функция |
( , , ) |
непрерывна |
в области |
|
то справедлива формула |
замены переменной в |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тройном интеграле: ( , , ) = [ ( , , ), ( , , ), ( , , )]∙||
9. Тройной интеграл в цилиндрической системе координат. Вычисление якобиана. Примеры.
= • φ∂ |
,∂ =∂ •∂φ∂ , |
∂ =∂ ; ≥0∂ |
,∂0≤φ≤2π, |
|||||||||||||||||
( , , ) = | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = |φ |
− φ 0 φ φ 0 0 0 1 | = ≥0 |
|
|
∂ ∂ ∂ ∂ |
∂ ∂ ∂ |
∂ |
||||||||||||||||
| ∂ |
| |
|
||||||||||||||||||
( , , ) = [ φ, φ, ]∙ φ
10. Тройной интеграл в сферической системе координат (два варианта). Вычисление якобиана. Примеры.
Сферическими координатами точки ( , , ) пространства называется тройка чисел , φ, θ, где
— длина радиуса-вектора точки , φ — угол, образованный проекцией радиуса-вектора на
плоскость и осью , θ — угол отклонения радиуса-вектора от оси .
= • φ • θ, = • φ • θ, = ∙ θ; ≥0, 0≤φ≤2π, 0≤θ≤π ( , , ) = |φ θ − φ θ φ θ φ θ φ θ φ θ θ 0 − θ | = φ( , , ) = ( φ θ, φ θ, θ)∙2θ∙ φ θ или
( , , ) = ( φ θ, φ θ, θ)∙2θ∙ φ θ
11.Приложения тройного интеграла.
●Объем области = = = φ = 2θ φ θ
●Масса тела = γ( , , )
●Статические моменты
|
= • γ( , , ) , |
= • |
γ( , , ) , = • γ( , , ) |
||||
● |
Координаты центра тяжести |
|
, |
|
|
, |
|
|
|
= |
= |
= |
|||
●Момент инерции
▪ относительно плоскостей = 2∙γ( , , ) , |
= 2∙γ( , , ) и |
= 2∙γ( , ) |
|
▪относительно координатных осей = (2 + 2)∙γ( , , ) ,
= (2 + 2)∙γ( , , ) и = (2 + 2)∙γ( , )
12. Криволинейный интеграл 1–го рода. Определение и свойства.
Криволинейным интегралом по дуге от скалярной функции ( , ) называется предел интегральной суммы при условии, что ∆ →0 при →∞:
∫ ( , ) = |
|
|
|
, |
|
∆ |
|
|
|
|
|
∑ |
|
|
|
непрерывна на кривой |
|
, то интеграл |
|||||
|
=1 |
|
|
|
|
( , ) |
|
|
|
||
|
|
|
|
|
|
|
|
||||
Теорема о существовании: Если функция |
|
|
|||||||||
существует. |
|
( |
|
|
|
) |
|
|
|
||
▪Если ( , , ) > 0, то крив интеграл ∫ ( , ) — масса кривой γ, где ρ = ( , ) —
переменная плотность (физ смысл)
▪Если ( , , )≥0, то крив интеграл ∫ ( , ) — площадь части цилиндр поверхности, у
которой направляющая лежит в плоскости , а образующая параллельна z; эта цилиндр поверхность ограничена сверху = ( , ), а снизу плоскостью (геом смысл)
Свойства:
●Не зависит от пути интегрирования ∫ ( , ) = ∫ ( , )
|
|
●∫ ∙ ( , ) = ∙ ∫ ( , ) , — const
● |
∫ |
( , ) + |
( , ) = ∫ |
( , ) + ∫ |
( , ) |
|
|
и |
|
, |
|
|||||||||
● |
|
|
|
|
||||||||||||||||
|
( |
1 |
2 |
|
) |
|
1 |
|
γ |
|
2 |
|
|
γ1 |
|
γ2 |
|
|
||
|
Если |
|
контур |
интегрирования |
|
разбит на |
две части |
|
|
|
|
то |
||||||||
|
∫ ( , ) = ∫ ( , ) + ∫ ( , ) |
|
|
|
|
|
|
|
|
|
||||||||||
|
γ |
|
|
γ1 |
|
|
γ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. Вычисление криволинейного интеграла 1–го рода. |
|
|
|
|
||||||||||||
● |
Если кривая задана |
= φ( ) |
: |
∫ ( , ) = ∫ ( , φ( )) |
1 + (φ'( ))2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
●Если кривая задана параметрически:
|
2 |
( '( ))2 + ( '( ))2 |
∫ ( , ) = ∫ ( ( ), ( )) |
||
● |
Если |
кривая |
|
задана |
|
1 |
|
в |
|
|
|
пространстве: |
|
|
|
2 |
|
|
'( ) 2 + '( ) 2 + '( ) 2 |
|
|
||||||
|
∫ ( , , ) = ∫ ( ( ), ( ), ( )) |
|
|
|
|||||||||
● |
|
1 |
∫ ( , ) = ∫ ( φ, φ) |
( |
2 |
+ '(φ) |
|
2 φ |
|||||
В полярных координатах: |
|
||||||||||||
|
( |
β ) |
( |
) |
|
) |
( |
) |
|
||||
|
|
|
|
α |
|
|
|
|
|
|
|||
14.Приложения криволинейного интеграла 1–го рода.
●Длина кривой: = ∫
●Площадь цилиндр поверхности:

Если ( , , )≥0, то крив интеграл ∫ ( , ) — площадь части цилиндр поверхности, у которой
направляющая лежит в плоскости , а образующая параллельна z; эта цилиндр поверхность ограничена сверху = ( , ), а снизу плоскостью
●Масса кривой:
Если ( , , ) > 0, то крив интеграл ∫ ( , ) — масса кривой γ, где ρ = ( , ) — переменная
плотность |
|
= ∫ ∙γ( , ) |
● Статические моменты: |
= ∫ ∙γ( , ) , |
|
|
|
|
●Координаты центров тяжести: = , =
● |
Моменты инерции: = ∫ |
2∙γ( , ) , = ∫ 2∙γ( , ) , |
= ∫ (2 + 2)∙γ( , ) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. Криволинейный интеграл 2–го рода. Определение и свойства. |
|
|||||||||||||||||||||||
Криволинейным |
интегралом |
|
|
от |
вектор-функции |
|
|
от |
векторного |
поля |
|||||||||||||||
→ |
|
|
|
→ |
|
|
|
→ |
по направленной дуге |
|
называется предел интегральной суммы |
||||||||||||||
( , ) = ( , ) + ( , ) |
|
|
|
|
→ |
|
^ |
^ |
|
|
|
^ |
^ |
|
|
|
|||||||||
при условии |
|
|
|
|
и |
|
|
|
|
: |
→ |
|
|
|
|
|
|
||||||||
∆ |
→0 |
∆ |
→0 |
∫ ( , ) = ∑ [ ( , |
)∆ |
|
+ ( |
, |
)∆ |
] |
|
||||||||||||||
Частные |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
||
|
|
случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∫ ( , ) = |
|
^ |
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∑ ( |
, )∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
=1 |
^ |
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫ ( , ) = ∑ ( |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Физический смысл — работа, совершенная переменной силой.
Свойства:
●∫ + =− ∫ +
● |
|
→ |
|
|
→ |
|
→ |
→ |
|
|
→ |
|
→ |
→ |
|
|
|
|
|
|
● |
∫ |
1 |
|
|
2 |
|
|
|
1 |
( , ) ± |
|
2 |
( , ) |
|
и |
|
, |
|
||
|
( , ) ± |
( , ) = |
∫ |
∫ |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
γ |
|
|
|
γ1 |
|
γ2 |
|
|
|
|
Если |
|
контур |
интегрирования |
разбит на две части |
|
|
то |
||||||||||||
|
|
→ |
|
→ |
|
→ |
→ |
|
→ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
||||||
|
∫ ( , ) = |
∫ ( , ) |
+ ∫ ( , ) |
|
|
|
|
|
|
|
|
|||||||||
|
γ |
→ |
→ |
γ1 |
→ |
|
γ2 |
|
|
|
|
|
|
|
|
|
|
|
||
● |
|
|
|
→, |
— const |
|
|
|
|
|
|
|
|
|||||||
|
∫ ∙ ( , ) |
= ∙ ∫ ( , ) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ + ∫ |
|
|
|
|
|
|||
● Крив интеграл по замкнутой кривой |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

16. Вычисление криволинейного интеграла 2–го рода.
●Кривая задана = , = φ( ): ∫ + = ∫[ ( , φ( )) + φ'( ) ( , φ( )) ]
|
|
2
●Параметрически: ∫ + = ∫[ ( ( ), ( ))∙ '( ) + ( ( ), ( ))∙ '( )]
|
1 |
17.Приложения криволинейного интеграла 2–го рода.
●Работа переменной силы 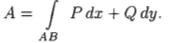
●Площадь плоской фигуры 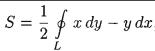
18.Условия независимости криволинейного интеграла 2–го рода от пути
интегрирования.

19. Формула Грина. Интегрирование полного дифференциала.

20. Поверхностный интеграл 1–го рода. Определение и свойства.
