
Матеша 3 семак.docx
.pdf
21. Вычисление поверхностного интеграла 1–го рода.
22. Приложения поверхностного интеграла 1–го рода.

23. Поверхностный интеграл 2–го рода. Определение и свойства.

24. Вычисление поверхностного интеграла 2–го рода (два варианта).

25.Приложения поверхностного интеграла 2–го рода.
●Объем тела 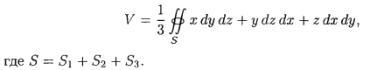
●
26. Формула Остроградского – Гаусса.
Если функции ( , , ), ( , , ), ( , , ) непрерывны вместе со своими частными производными первого порядка в пространственной области , то справедлива формула Остроградского-Гаусса:
( ∂∂ + ∂∂ + ∂∂ ) = + + , где — граница области и
интегрирование по производится по ее внешней стороне.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
27. |
|
Формула Стокса. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если |
функции |
( , , ) |
, |
|
|
( , , ) |
, |
( , , ) |
непрерывны |
вместе |
со своими |
частными |
||||||||||||||||||||||||
производными |
|
|
|
|
|
|
|
и |
|
— замкнутый контур, ограничивающий |
||||||||||||||||||||||||||
|
|
|
|
|
|
первого порядка на поверхности |
||||||||||||||||||||||||||||||
поверхность |
|
, то справедлива формула Стокса: |
|
|
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
∂ |
|
|
|
|
∂ |
|
∂ |
|
|
|
|
|
|
|
|
γ |
|
||||||
, |
+ , |
|
+ |
= |
|
|
|
− |
|
|
|
α + |
|
|
|
− |
|
|
|
β + |
|
|
|
|
− |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
∂ |
|
|
|
|
∂ |
|
∂ |
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
||||
α β γ |
— направляющие косинусы нормали к поверхности |
|
. Направление нормали: со |
|||||||||||||||||||||||||||||||||
|
|
|
|
( |
|
|
|
) |
|
( |
|
|
|
|
) |
|
|
( |
|
|
|
) |
|
|
|
|||||||||||
стороны нормали обход контура против часовой стрелки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
28. Понятие скалярного поля, его характеристики. |
|
|||||||||||||||||||||||||||||
Скалярное поле - часть пространства, в каждой |
точке |
( , , ) |
|
которого задана |
скалярная |
|||||||||||||||||||||||||||||||
функция |
= ( , , ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поверхность (линия) уровня скалярного поля есть геометрическое место точек, в которых функция
принимает постоянное значение, |
т.е |
( ) |
= |
. Для плоского поля |
= ( , ) |
линия уровня |
||||
|
, для пространственного |
|
|
|
|
|||||
= ( , ) |
|
поля |
= |
( , , ) |
поверхность уровня |
= ( , , ) |
||||
|
|
|
|
|
||||||
29. Понятие векторного поля. Векторные линии и векторные трубки.
Если в некоторой области пространства каждой точке M по определённому закону
ставится в соответствие вектор |
→ |
, то векторная функция |
→ |
называется полем вектора |
или векторным полем/ |
|
|
( ) |
|
Совокупность всехв екторныхлиний, про ходящих через точки куска поверхности вращения S, называются векторнойтр убкой.
30. Дивергенция векторного поля, ее свойства.

Дивергенция (расходимость) – характеристика вект-го поля, определяющая распределение и интенсивность источников и стоков поля: дивергенциейв т очке М
называется скаляр вида |
∂∂ |
+ |
∂∂ |
+ |
∂∂ |
и обозначается: |
||||||
→ |
∂ |
∂ |
∂ |
|
|
|
|
|
|
|
||
( ) = |
∂ |
+ |
∂ |
+ |
∂ |
|
|
|
|
|
|
|
Св-ва дивергенции: |
|
|
|
|
|
|
|
|
||||
1.если →- постоянный вектор, то |
|
→ |
|
|
. |
|||||||
|
|
∂∂ |
||||||||||
|
|
|
|
|
|
|
|
( ) = |
|
|||
→→
2.(∙)= ∙ , где с=const.
3. |
|
→ → |
|
→ |
, т.е. дивергенция суммы 2-х векторных функций равна |
сумме дивергенции слагаемых. |
|
||||
|
|
+ |
= + |
→- вектор, то |
|
4.если(U – скалярная) |
функция, |
||||
|
|
→ |
→ |
→ |
. |
(∙)= ∙ +
31. Ротор векторного поля, его свойства.
32. Соленоидальное векторное поле, его свойства.
Векторное поле называется соленоидальным, если дивергенция вектора в каждой точке
→
поля равна нулю: ( ) = 0., т.е. в области заданного поля V отсутствуют и стоки, и источники.
Свойства:
→
1). Поле является соленоидальным тогда и только тогда, когда
→
( ) = 0.

2). В соленоидальном поле поток через замкнутую поверхность, не содержащую внутри особых точек поля, равен нулю.
3). В соленоидальном поле потоки через замкнутые поверхности, окружающие все особые точки поля, равны между собой.
4). В соленоидальном поле поток через любое поперечное сечение векторной трубки сохраняет постоянное значение (называемое интенсивностью трубки)
33. Потенциальное векторное поле, его свойства.
Потенциальное (или безвихревое)в екторноепо лев м атематике —в екторноепо ле, которое можно представить как градиент некоторой скалярной функции координат.
→
=
При этом выполняются равенства:
= ∂∂ , = ∂∂ , = ∂∂
Свойства:
1.Потенциал определён с точностью до произвольной постоянной gradφ=grad(φ+C)
2.Разность потенциалов в двух точках M1 V,M2 V определена однозначно.
3.Если поле по тенциально, то линейный интеграл этого поля по любой кривой целиком лежащей в V , определяется только начальной и конечной точками этой кривой и не зависит от формы кривой.
4.Циркуляция потенциального в области V поля по любому контуру, лежащему в V, равна нулю.
5.Векторная линия потенциального поля в каждой точке M ортогональна эквипотенциальной поверхности (поверхности уровня потенциала), проходящей через точку M.
6.Ротор потенциального векторного поля равен нулю.
34. Операции второго порядка в векторном анализе. Оператор Гамильтона.

ОператорГ амильтона — векторный дифференциальныйопера тор, компоненты которого являются частными производными по координатам.
∂→ ∂ → ∂ →
= ∂ + ∂ + ∂
35.Понятие числового ряда, сходимости и суммы. Необходимый признак.

36. Простейшие свойства сходящихся рядов.

Теорема 1 (о почленном умножении ряда на число). |
Если ряд ∞ |
сходится и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
, то ряд ∞ |
|
|
|
|
|
|
|
|
=1 |
|
||
имеет сумму |
, где с – постоянная, также сходится и имеет |
|||||||||||||||
сумму . |
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
а 2 (о почленном сложении сходящихся рядов). Пусть числовые ряды |
|||||||||||||||
Теорем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
и ∞ |
|
|
сходятся и имеют суммы |
|
и |
|
соответственно. Тогда ряд |
||||||||
∑ |
∑ |
|
|
|
|
|
|
|
|
|
|
|
||||
=1 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
т акже сходится, и его сумма равна |
|
+ |
. |
|
|||||||||
∑ + |
|
|
|
|
|
|
|
|
|
|
|
|
||||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение( ). Если у ряда (1) |
∞ |
отбросить k первых членов, то получится |
||||||||||||||
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
новый ряд |
|
|
|
, называемый k-ым остатком ряда (1). |
|
|||||||||||
Теорема 3. |
Ряд (1) и любой из его остатков либо одновременно сходятся, либо |
|||||||||||||||
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= +1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
одновременно расходятся.
37. Гармонический ряд. Геометрический ряд.
38. Признаки сравнения рядов с положительными членами.
