2.2 Нахождение экстремального значения функции f(X) с учетом системы ограничений задачи Метод допустимых направлений Зойтендейка

Условие задания:

=[4;4]

Здесь решение совпадает с первой итерацией метода наискорейшего спуска (подъёма). Найдем градиент F(x):

.

Тогда координаты очередной точки:

Здесь решение совпадает с первой итерацией метода наискорейшего спуска (Подъёма), тогда:

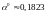
Определяем интервал допустимых значений для ⁰, при котором точка x¹ будет принадлежать ОДЗП. Для этого подставим координаты точки x¹ в ограничения задачи:

=>

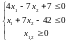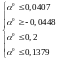
Тогда:

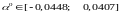
Находим величину ,которая обеспечит экстремум функции F(x). Воспользуемся уже найденным =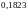 , но т.к. оно не входит в наш интервал, то =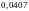 При этом очередная точка поисковой траектории оказывается на границе области. Координаты точки и значение градиента функции в этой точке определяются выражениями

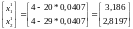
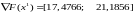
Движение в направлении градиента выводит за пределы ОДЗП, поэтому очередную точку поиска вычисляем исходя из выражения:

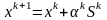
где 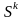- новое направление, которое составляет минимальный острый угол с вектором градиента и направлено либо внутрь, либо по границе ОДЗП. При этом очередная точка должна принадлежать ОДЗП, а функция цели при переходе к очередной точке должна уменьшаться максимальным образом.

Направление находим, как решение задачи:

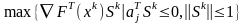
Найдем направление 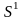очередного шага: т.к. x¹ лежит на , то услови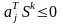е (где 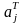- вектор коэффициентов при переменных в первом ограничении, на котором находится точка x¹) запишется:

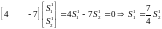
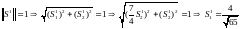
При движении из точки x¹ в точку x² следует двигаться по граничной прямой в направлении .

Координаты точки x² определяются выражением:

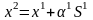
или

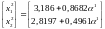
Находим интервал изменения , при котором точка принадлежит ОДЗП, причем ограничение отбросим:

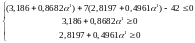
Получим интервал:

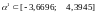
Найдем такое ¹ , которое обеспечит максимум F(x) в направлении . Для этого координаты точки x² подставляются в функцию F(x),тогда:

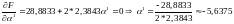
Значение ¹ не принадлежит ранее найденному интервалу, поэтому для расчета координат точки принимается = :

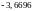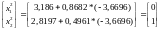
_{Мы находимся в точке экстремума функции с учетом ограничений. А значение функции цели в этой точке равно:}

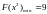
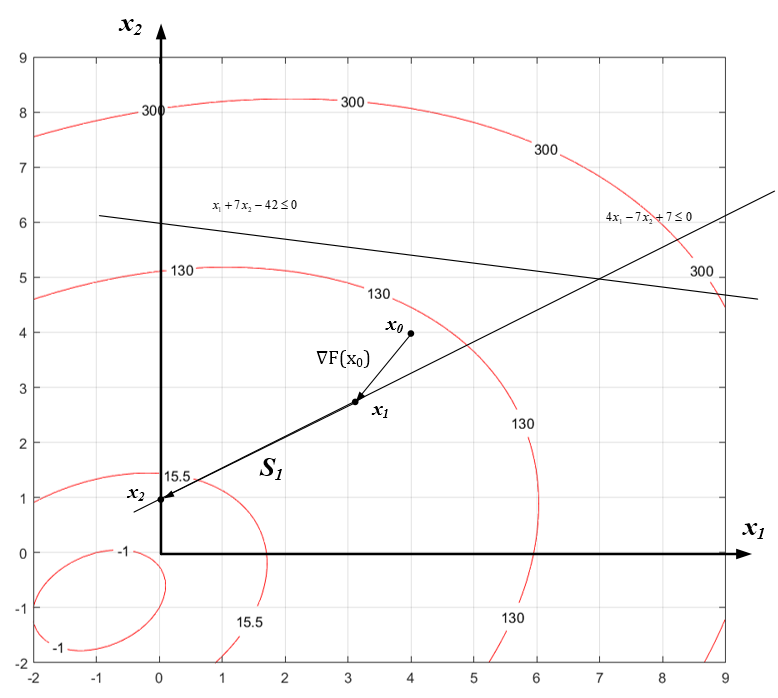
Рисунок 2.5 - Графическая интерпретация метода Зойтендейка

Метод линейных комбинаций

Условие задания:

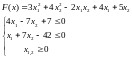
=[4;4]

Вычислим градиент функции F(x):

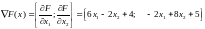
На следующем этапе вычислим значение градиента в точке x₀:

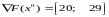
Суть метода линейных комбинаций заключается в линеаризации функции F(x) и замене ее линейной функцией в соответствии с выражением:

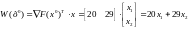
Решаем задачу линейного программирования при следующих ограничениях:

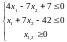
Процедура решения задачи иллюстрируется следующей симплекс таблицей:

Таблица 3.1

БП	Своб. члены	НП
		x1	x2
x3	-7	4	-7
x4	42	1	7
W	0	20	29

Таблица 3.2

БП	Своб. члены	НП
		x1	x3
x2	1	-0,5714	-0,1428
x4	35	5	1
W	0	-35,5714	-4,1429

Получено оптимальное допустимое решение, которое имеет вид:

Произведем корректировку найденного решения в соответствии с выражением:

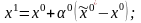
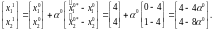
Найдем значение , которое доставляет экстремальное значение функции F(x¹):

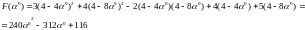
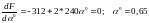
Определяем интервал допустимых значений для ⁰, при котором точка x¹ будет принадлежать ОДЗП. Для этого подставим координаты точки x¹ в ограничения задачи:

=>

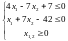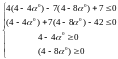
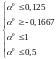
Тогда:

Величина 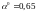, не входит в наш интервал, тогда =0,5. Координаты точки и значение градиента функции в этой точке определяются выражением

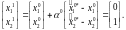
Значение функции цели в этой точке равно:

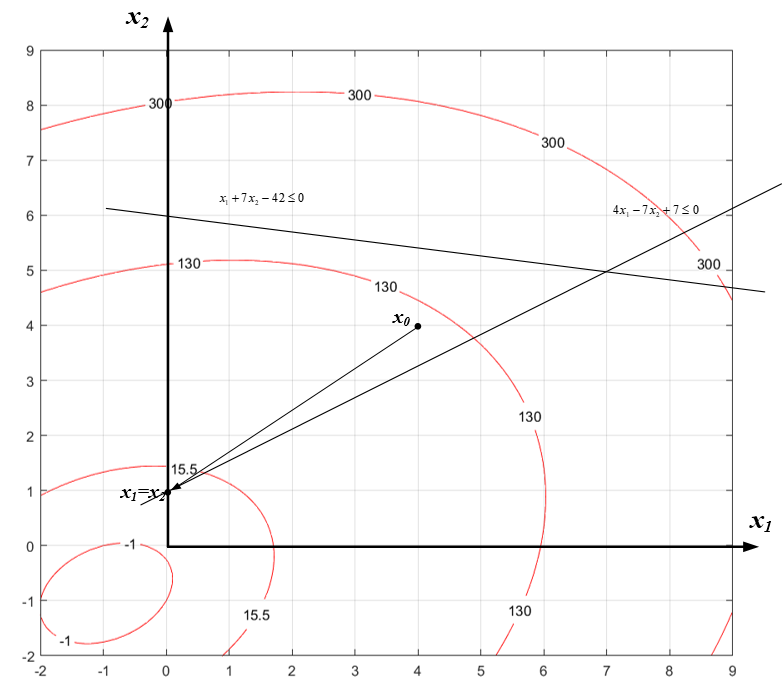
Рисунок 2.6 - Графическая интерпретация метода линейных комбинаций.