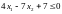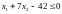2. Нелинейное программирование Построение одзп, выбор начальной точки поиска

Целевая функция имеет вид:

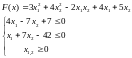
Вид функции можно посмотреть в пакете Matlab, используя следующую подпрограмму: >> [x1,x2]=meshgrid([-10:0.1:10]); >> F=3*x1.^2+4*x2.^2-2*x1.*x2+4*x1+5*x2; >> meshc(x1,x2,F);

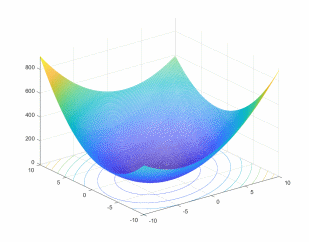
Рисунок 2.1 – Вид функции цели

Функция вогнута и имеет минимум.

Построим ОДЗП:

1. 

Пусть x₁=7, тогда x₂=5

Пусть x₁=0, тогда x₂=1

2. 

Пусть x₁=7, тогда x₂=5

Пусть x₁=0, тогда x₂=6

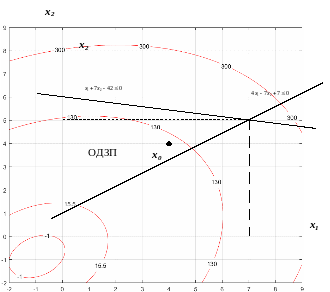
Рисунок 2.2 – ОДЗП

Внутри области допустимых значений выбираем точку x⁰, которая в дальнейшем будет являться начальной в процессе поиска экстремума:

x⁰=(4;4).

2.1 Нахождение экстремального значения функции f(X) без учета ограничений на переменные Метод наискорейшего спуска

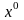=[4;4]

В методе наискорейшего спуска очередная точка при поиске минимума функции вычисляется по формуле:

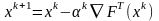
где направление движения задается вектором градиента 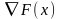функции F(x), вычисленном в точке 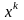, а величина шага перемещения определяется числовым параметром .

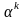Найдем градиент :

.

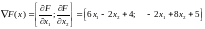
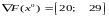На первом шаге движение осуществляется из точки вдоль вектора

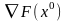- в новую точку :

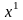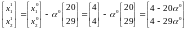
В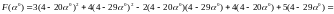 еличина шага на любом шаге выбирается из условия обеспечения экстремума функции в рассматриваемом направлении. Подставляя координаты точки в функцию 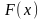, получим:

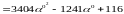
Из условия:

;

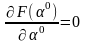найдем :

;

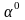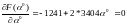
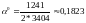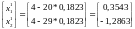
В результате после первого шага координаты очередной точки получаются равными:

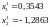
Вычисляем

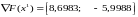
На втором шаге движение осуществляется в направлении вектора

- :

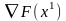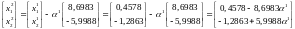
Подставив полученные выражения для x12 и x22 в функцию цели и преобразовав, из условия

;

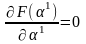найдем :

;

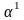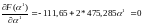
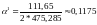Тогда:

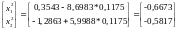
В результате после второго шага координаты очередной точки получаются равными:

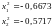
Вычисляем :

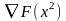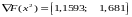
На третьем шаге движение осуществляется в направлении вектора

- :

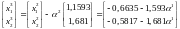
Подставив полученные выражения для x12 и x22 в функцию цели и преобразовав, из условия:

;

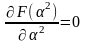найдем :

;

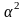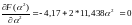
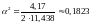В результате после третьего шага координаты очередной точки получаются равными:

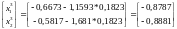
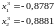
На третьей итерации закончим вычисления, значение функции цели:

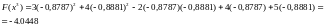
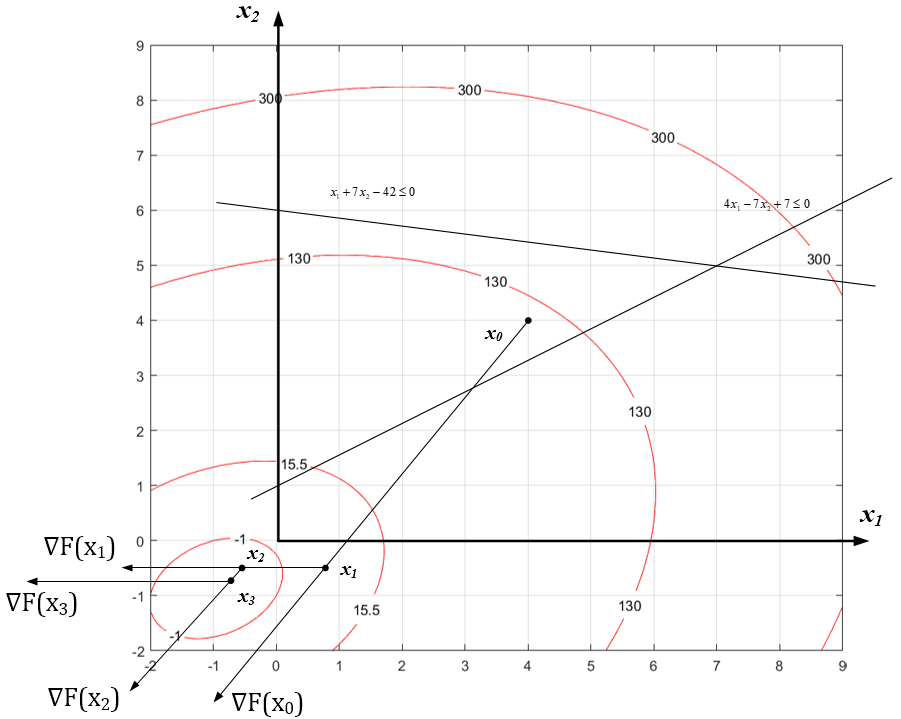
Рисунок 2.3 – Графическая интерпретация метода наискорейшего спуска

Метод Ньютона-Рафсона

Условие задания:

=[4;4]

Данный метод дает решение задачи за 1 шаг. Очередная точка поиска вычисляется в соответствии с выражением:

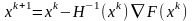
где 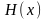– матрица Гессе функции ; 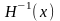– обратная по отношению к матрица.

Градиент F(x):

;

.

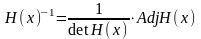
где det H – определитель матрицы H; AdjH – присоединенная к H матрица (транспонированная матрица алгебраических дополнений).

Найдем определитель матрицы Гессе:

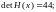
Найдем транспонированную матрицу алгебраических дополнений AdjH:

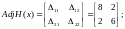
Теперь найдем матрицу обратную по отношению к 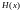- матрицу :

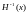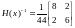
тогда:

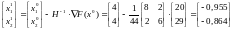
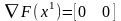
Следовательно, в точке 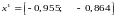функция F(x) достигает экстремального значения:

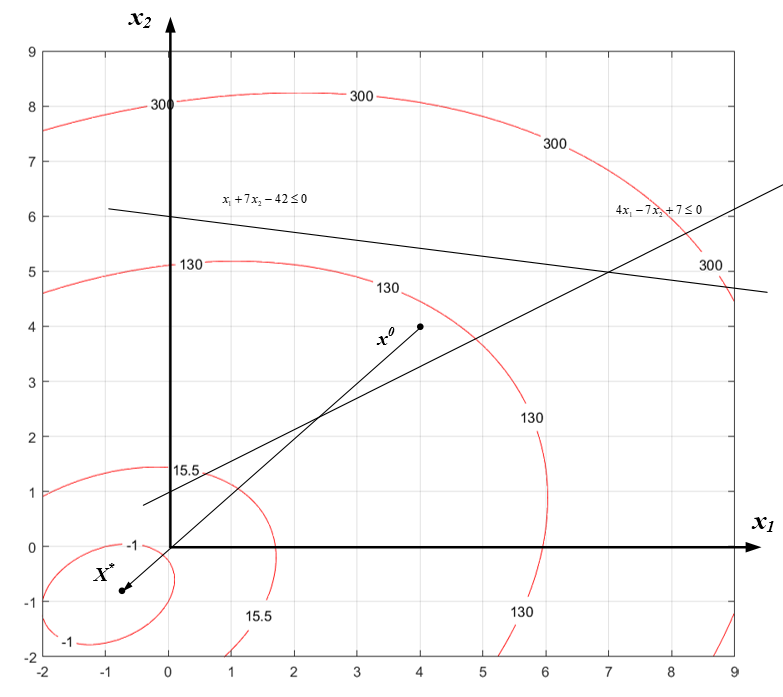
Рисунок 2.4 – Графическая интерпретация метода Ньютона-Рафсона