
727
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
8 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
n 1 |
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
3 |
|
|
|
8 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n |
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n (n 1) |
|
3 |
|
|
|||||||||||||||
8 |
|
|
|
|
1 |
8 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n |
|
3 |
|
|
|
|
|
|
|
|
|
n |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

 89 1. Ряд сходится. Значит, данный ряд с комплексными членами сходится абсолютно.
89 1. Ряд сходится. Значит, данный ряд с комплексными членами сходится абсолютно.
(2 3i)n
г) Для исследования на сходимость ряда
n 1 (3 i)2n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 32 |
|
|
|
||||||
составим |
|
ряд |
|
из |
|
модулей: |
|
|
2 3i |
|
|
13 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
32 |
( 1)2 |
|
|
|
|
|
|
|
13 |
|
|
13 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
3 i |
|
|
10 |
, |
|
|
|
|
|
. |
По |
ради- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 10) |
2n |
|
|
|
10 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
|
|
|
|
|||||||||
кальному |
признаку |
|
|
Коши |
этот |
числовой |
ряд |
сходится: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
lim |
n |
|
|
lim |
|
|
1. Значит, ряд с комплексными чле- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
n |
|
|
10 |
|
|
n |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
нами абсолютно сходится. В теории рядов с комплексными членами основные
В теории рядов с комплексными членами основные
определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами. А также при исследовании на сходимость рядов с комплексными членами применимы все известные признаки сходимости знакопостоянных рядов.
49. Исследовать на сходимость ряды:
а)
г)
|
|
2 i |
|
n2 |
|
|||
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||
n 1 |
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
n i |
|
|
|
|||
|
|
|
; |
|
||||
n 1 |
|
|||||||
n 1 |
|
|
|
|||||
Решение.
|
n |
n |
|
б) |
|
; |
|
|
|
||
|
|
||
n 1 n!(e i)n |
|
||
in
д) ;
n 1 n
в)
е)
|
n(2 i)n |
|
|
|
|
|
|
|
|
; |
|
|
|
|
2n |
|
|
|
||
n 1 |
|
|
|
|
|
|
|
|
n(2 i) 1 |
|
n |
||
|
||||||
|
|
|||||
|
|
|
|
. |
||
|
|
|
||||
n 1 |
n(3 2i) |
3i |
|
|||
71

|
2 |
i |
n2 |
||
а) Для исследования на сходимость ряда |
|
|
|
|
|
|
|
|
|||
n 1 |
3 |
|
|||
применим радикальный признак Коши:
|
|
|
|
|
|
|
|
2 i n2 |
|
|
|
2 i |
|
|
n2 |
|
|
|
2 i |
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
n |
n |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
n |
zn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
. |
Тогда |
|
|
lim n |
|
|
z |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
9 |
|
|
|
|
3 |
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
му ряд абсолютно сходится.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 |
|
2 |
|
|
1 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||
lim |
|
|
|
|
|
0 1 |
поэто- |
||||||||||||
|
|
|
|
||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
б) Для исследования на сходимость ряда |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n!(e i)n |
|
|
|||||
применим признак Даламбера: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
zn |
|
|
|
|
nn |
|
|
|
, zn 1 |
|
|
|
(n 1)n 1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
n!(e i)n |
|
|
|
(n 1)!(e i)n 1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
|
z |
n 1 |
|
lim |
|
|
(n 1)!(e i)n 1 |
|
|
lim |
|
(n 1)n (n 1)n!(e i)n |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
zn |
|
|
|
|
|
|
|
|
nn |
|
|
|
|
|
|
|
|
n!(n 1) (e i)n (e |
i)nn |
|
|||||||||||||||||||||||||||
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!(e i)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
|
|
(n 1)n |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
n 1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
i)nn |
|
|
e i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
n |
(e |
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
0,939 1, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
e2 ( 1)2 |
n |
|
|
|
n |
|
|
|
|
|
|
e2 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
поэтому ряд сходится абсолютно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
(В |
|
примере |
|
|
|
|
использован |
второй |
|
|
замечательный |
предел |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
|
1 |
|
|
|
e ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
в) Применим признак Даламбера. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
zn |
|
n(2 i)n |
, zn 1 |
(n 1)(2 i)n 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
2n |
|
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
72

|
|
|
|
|
|
|
|
|
|
|
|
(n 1)(2 i)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
lim |
zn 1 |
|
lim |
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
lim |
(n 1)(2 i)n (2 i)2n |
|
|
||||||||||||||||||
zn |
|
|
|
|
n(2 i)n |
|
|
|
|
|
|
|
2n 2 n(2 i)n |
||||||||||||||||||||||||
n |
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 i |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
lim |
|
|
|
|
5 |
1, поэтому ряд расходится. |
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
n |
n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
г) |
|
Представим ряд |
|
в виде суммы двух рядов с |
|||||||||||||||||||||||||||||
|
|
|
|
|
n 1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
|
|
|
|||||||
действительными членами |
|
|
|
i |
|
. Сравним первый |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n 1 |
n 1 n |
1 |
|
|
||||||||||||
из них с расходящимся обобщенным гармоническим рядом
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n |
|
|
|
|
|
|
|
||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
n n |
|
|
||
lim |
|
|
n 1 |
|
lim |
|
|
1 const 0 , первый ряд расходится. |
|||||||||
|
|
|
n 1 |
|
|||||||||||||
n |
|
|
1 |
|
|
|
n |
|
|
||||||||

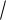 n
n
Второй ряд сравним с расходящимся гармоническим рядом
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
: |
lim |
|
|
|
lim |
|
|
|
|
|
1 |
const 0 , второй ряд также |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
n 1 n |
n |
|
|
1 |
|
|
|
|
|
|
n n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, исходный ряд также расходится. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
|
|
д) Представим исследуемый ряд |
i |
|
|
в виде суммы двух |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n |
|
|
|
||||
знакочередующихся рядов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
in |
|
i |
|
|
1 |
|
|
|
i |
|
1 |
|
i |
|
1 |
|
|
i |
|
1 |
|
|
( 1)n |
|
( 1)n 1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
i |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
||||||||||||||||
n 1 |
|
n 1 2 3 |
|
4 5 6 7 8 |
n 1 |
|
2n |
n 1 |
|
||||||||||||||||||||||||||||||
Оба числовых ряда с действительными членами сходятся согласно признаку Лейбница. Составим ряд из модулей членов
73

|
|
i |
n |
|
|
1 |
|
|
|
|
|
ряда: |
|
|
|
|
, он расходится. |
||||||
|
|
|
|||||||||
|
n 1 |
n |
|
n 1 n |
|
|
|
|
|||
ряд сходится условно. |
|
|
|||||||||
|
|
|
|
|
|
|
|
n(2 i) 1 |
|
n |
|
|
|
|
|
|
|
|
|
||||
е) |
Для ряда |
|
|
||||||||
|
|
|
|
||||||||
|
|
||||||||||
|
|
|
|
|
|
n 1 |
n(3 2i) 3i |
|
|||
признак Коши:
Следовательно, исходный
используем радикальный
|
|
|
|
|
lim |
|
|
|
|
|
n(2 i) 1 n |
lim |
|
(2 i)n 1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
lim n |
|
zn |
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
n |
|
|
|
n |
|
|
|
n(3 |
2i) 3i |
n |
(3 |
2i)n 3i |
|
|
|||||||||||||
|
|
|
2 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
|
|
|
5 |
|
|
|
|
5 |
|
1, ряд сходится абсолютно. |
|||||||||||||||
|
3 2i |
|
|
|
|
|
|
|
13 |
||||||||||||||||||
|
13 |
||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2. Степенные ряды с комплексными членами
Степенным рядом с комплексными членами
называется ряд вида
c0 c1 (z a) ... cn (z a)n ... cn (z a)n ,
n 0
где z – комплексное переменное, cn и а – комплексные или действительные числа.
При а = 0 имеем ряд вида c0 c1z ... cn z n ... cn z n .
n 0
Точки z, в которых ряд сходится, образуют область сходимости данного ряда. Поскольку комплексные числа на комплексной плоскости хОу представляются точкой, то область сходимости степенного ряда представляет собой круг.
Теорема Абеля. Если степенной ряд в комплексной области сходится в точке z0 0, то он сходится абсолютно в любой точке, лежащей внутри круга радиуса R z0 с цен-
тром в точке а для ряда cn (z a)n и с центром в начале
n 0
74
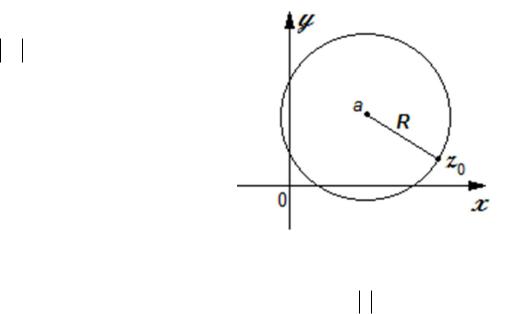
координат для ряда cn z n . Если же ряд расходится в неко-
n 0
торой точке z0 , то он расходится во всех точках плоскости хОу, удаленных от точки а на расстояние большее,
чем z0 .
То есть для каждого степенного ряда существует круг радиуса R, внутри которого ряды сходятся абсолютно (рис.3). Вне круга ряды расходятся. В точках границы круга схо-
димости степенной ряд Рис.3 может как сходиться, так и расходиться.
R – радиус круга сходимости, если z R для ряда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cn z n |
|
и если |
|
|
z a |
R для ряда cn (z |
a)n . |
|
||||||||||||||||||||||||||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если R 0, ряд сходится только в одной точке. |
|
||||||||||||||||||||||||||||||||||
Если R , |
ряд сходится во всех точках комплексной плос- |
||||||||||||||||||||||||||||||||||
кости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Для поиска R можно использовать признак Даламбера |
||||||||||||||||||||||||||||||||
или радикальный признак сходимости Коши. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Областью сходимости степенного ряда по отрицатель- |
||||||||||||||||||||||||||||||||
ным степеням z – a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
b1 |
|
|
|
b2 |
|
|
|
|
|
bn |
|
|
|
|
|
bn |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
... |
|
|
|
... |
|
является внеш- |
||||||||||||||||||||||
|
|
|
|
z a 2 |
|
|
z a n |
|
|
a n |
|||||||||||||||||||||||||
|
z a |
|
|
|
|
|
|
n 1 z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ность круга с центром в точке а некоторого радиуса R. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Если ряд |
cn (z a)n |
|
сходится в круге |
|
|
|
z a |
|
|
|
R , |
а ряд |
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn (z a) n |
|
|
сходится |
|
в |
области |
|
|
z a |
|
r , то |
при |
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 r R областью сходимости ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
cn (z a) |
n |
является кольцо r |
|
z a |
|
R ; |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
z a n |
|
|
|
|
||||||||||||||||||||||||||||||
n 1 |
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

при r > R этот ряд всюду расходится.
50. Найти круг и радиус сходимости ряда
z n |
|
|
|
|
|
|
|
|
|
|
|
|
|
in |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z 2i)n |
|
|
|
|||||||||||||||
а) |
|
|
|
|
; |
|
|
|
|
|
б) |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
n 0 n! |
|
|
|
|
|
|
|
|
n 0 z n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
n3n |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!(1 i) |
|
|
|
|
|
|
|
|
|
(2i)n 1 (z 3i)n |
|
||||||||||||||||||||||||||
г) (n! i)z3n ; |
|
|
|
|
д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2n ; |
|
|
|
е) |
|
|
|
|
|
|
. |
||||||||||||||||||||||
|
|
|
|
(2n 1)! |
|
|
|
|
|
|
3i)n |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
( 7 |
|||||||||||||||||||||||||||||||||||||||||||||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||||||||||||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) Для ряда |
z |
|
|
применим признак Даламбера. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n 0 n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z n 1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z |
, zn 1 |
|
z |
|
|
|
|
|
|
zn 1 |
|
lim |
|
(n 1)! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
zn |
|
|
|
|
|
|
|
. |
|
lim |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
zn |
|
|
|
z n |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
n! |
|
|
(n 1)! |
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
|
|
|
zn z n! |
|
lim |
|
z |
|
|
|
|
|
z |
|
lim |
|
1 |
|
|
|
|
|
z |
|
|
0 1, |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
n!(n 1)zn |
|
|
n 1 |
|
|
|
|
n 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поэтому ряд абсолютно сходится при любых значениях z, то есть в любой точке комплексной плоскости, R .
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) Для ряда |
|
i |
|
|
|
применим радикальный признак схо- |
||||||||||||||||||||||||||||||||
n |
||||||||||||||||||||||||||||||||||||||
|
n 0 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim n |
|
in |
|
lim |
|
|
|
|
|
|
|
|
|
|
02 12 |
|
|
1 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|||||||||||||||||
димости Коши: |
lim n |
|
zn |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
zn |
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
z |
|
|||||||||||||||||||
|
n |
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Согласно признаку Коши, ряд сходится при |
1 |
|
|
1 |
|
z |
|
|
1 – |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
z |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
внешняя часть круга с центром (0,0) радиуса 1. На границе
|
n |
|
этого круга ряд принимает вид: |
i |
in и расходится, |
n |
||
n 01 |
n 0 |
|
т.к. для него не выполняется необходимый признак сходимости.
|
(z 2i)n |
|
|
в) По признаку Даламбера для ряда |
|
: |
|
n3n |
|||
n 0 |
|
||
76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z 2i)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
lim |
|
z |
n 1 |
|
|
lim |
|
(n 1)3n 1 |
|
|
|
lim |
(z 2i)n (z 2i)n 3n |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
zn |
|
|
|
|
|
|
|
|
|
2i)n |
|
|
|
|
|
|
|
(n 1)3n 3(z 2i)n |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
n |
|
|
n |
|
|
(z |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n3n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
z 2i |
|
|
lim |
|
|
|
|
n |
|
|
|
|
|
|
|
z 2i |
|
, |
|
|
поэтому |
|
круг |
сходимости при |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
n |
|
1 |
|
|
|
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
z 2i |
|
|
1 |
|
z 2i |
|
|
3 – |
|
круг с центром (0; |
2) комплексной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
плоскости, радиуса R 3. Вне этого круга ряд расходится. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На границе круга сходимости |
|
z 2i |
|
|
|
|
3 ряд расходится, |
т.к. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
n |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
принимает вид: |
|
|
|
|
|
|
|
|
– расходящийся гармонический |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 n3n |
|
|
|
|
n 0 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ряд (1.6.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) По признаку Даламбера для ряда (n! i)z3n : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
z |
n 1 |
|
|
lim |
|
((n 1)! i)z3(n 1) |
|
|
lim |
|
(n!(n 1) i)z3n z3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
zn |
|
|
|
|
|
|
|
|
|
(n! i)z3n |
|
|
|
|
|
|
|
|
(n! i)z3n |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
z |
|
|
|
3 lim |
|
n!(n 1) i |
|
|
1, |
|
поэтому радиус круга сходимо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n! i |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
сти R 0 , ряд сходится только в одной точке (0; 0). |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!(1 i) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
д) По признаку Даламбера для ряда |
|
|
|
|
|
|
z 2n : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2n 1)! |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1)!(1 i) |
|
z |
2(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
lim |
|
zn 1 |
|
|
lim |
|
(2(n 1) |
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n!(1 i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
n |
|
z |
n |
|
n |
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n 1)! z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
n!(n 1)(1 i)z2n z2 (2n 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(2n 1)!n!(1 i)z2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 lim |
|
(n 1)(2n 1)! |
|
|
|
|
|
|
|
|
|
|
(n 1) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
z 2 lim |
|
|
|
|
|
z 2 |
0 0 1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
(2n 1)!(2n)(2n 1) |
|
2n(2n |
1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
поэтому |
|
радиус круга |
|
сходимости |
R , ряд сходится |
во |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
всех точках комплексной плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2i)n 1 |
(z 3i)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
е) Для ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
применим радикальный |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3i)n |
||||||||||||||||||||||||||||||||||||||||||||
( 7 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
признак сходимости Коши: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim n |
|
|
(2i)n 1(z 3i)n |
|
lim |
|
|
|
z 3i |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
lim n |
zn |
|
|
|
|
|
|
|
|
|
(2i) n |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
( 7 3i)n |
|
|
|
|
|
7 3i |
||||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
02 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
z 3i |
|
lim |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
)2 ( 3)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
( |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
z 3i |
|
|
|
2 |
|
|
|
|
z 3i |
|
|
1 |
|
z 3i |
|
2 – круг с центром (0; – 3), |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
радиусом 2, внутри которого степенной ряд с комплексными членами сходится абсолютно.
Контрольные вопросы № 2
1.Дайте определение функционального ряда и области его сходимости.
2.Дайте определение степенного ряда и области его сходимости.
3.Теорема Абеля для степенного ряда.
4. Чему равен радиус сходимости степенного рядааn xn , если:
а) ряд сходится только при х = 0, б) ряд сходится при любом значении х?
5. Приведите формулы нахождения радиуса сходимости степенного ряда аn xn в случае, когда степенной ряд со-
держит все степени х.
6. Приведите алгоритмы нахождения области сходимости степенного ряда аn xn в случае, когда степенной ряд содержит не все степени х.
7.Теоремы о дифференцировании и интегрировании степенных рядов.
8.Дайте определения рядов Тейлора и Маклорена.
9.Приведите формулы разложений элементарных функций в степенной ряд.
78
10.Алгоритмы применения рядов к приближенным вычислениям корней, значений тригонометрических функций, логарифмов.
11.Применение рядов к решению дифференциальных уравнений и к приближенным вычислениям определенных интегралов.
12.Может ли интервал сходимости ряда аn xn быть та-
ким: а) (–2; 0); б) (–3; 1); в) (–3; 3); г) (0; 2); д) ( ; ) .
13.Известно, что ряд аn (x 3)n в точке x = 2 расходит-
n 1
ся. Что можно сказать о сходимости ряда в точке:
а) х = 5; б) х = 3,5; в) х = 4.
14.Известно, что ряд аn (x 3)n в точке x = 2 абсолют-
n 1
но сходится. Что можно сказать о сходимости ряда в точке:
а) х = 5; б) х = 3,5; в) х = 4.
15.Существует ли степенной ряд, для которого верно следующее утверждение:
а) на обоих концах интервала сходимости ряд расходится; б) на одном конце интервала сходимости ряд сходится условно, а на другом – сходится абсолютно;
в) на обоих концах интервала сходимости ряд сходится абсолютно; г) на одном конце интервала сходимости ряд сходится услов-
но, а на другом – расходится; д) на одном конце интервала сходимости ряд сходится абсо-
лютно, а на другом – расходится.
16.Дайте определение числового и степенного ряда с комплексными членами.
17.Дайте определение сходящегося и расходящегося ряда
скомплексными членами. Приведите примеры сходящихся и расходящихся рядов.
18.Абсолютная и условная сходимость рядов с комплексными членами.
19.Теорема Абеля для степенного ряда с комплексными членами.
79
ГЛАВА 3. Ряды Фурье
§10. Ряды Фурье для периодических функций 3. Периодические функции. Периодические процессы
При изучении разнообразных периодических процессов, т.е. процессов, которые через определенный промежуток времени повторяются (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т.д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Простейшими периодическими функциями являются тригонометрические функции sin x и cos x. Период этих функций равен 2 . Простейшим периодическим процессом
(движением) является простое гармоническое кол е -
бание (движение), описываемое функцией y A sin( t 0 ) , где t 0, А – амплитуда колебания, – частота, 0 – началь-
ная фаза. Функцию такого вида (и ее график (рис.4)) называ-
ют простой гармоникой .
Рис.4
Основным периодом такой функции является T 2 , т.е. од-
но полное колебание совершается за промежуток времени Т. Преобразуем функцию у.
y A sin( t 0 ) A sin t cos 0 A cos t sin 0 ,
y a cos t b sin t , где a Asin 0 , b Acos 0 . Отсюда видно, что простое гармоническое колебание описывается периодическими функциями sin t и cos t .
Сложное гармоническое колебание , возникаю-
щее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида sin t и cos t . Например, функция, задающая сложное гармоническое колебание:
80
