
10546
.pdf
lim |
y = lim y |
x = lim y |
lim |
x = f ′(x) 0 = 0. |
x→0 |
x→0 x |
x→0 x |
x→0 |
|
Как мы видим, из существования производной |
f ′(x) следует равенство |
|||
lim y = 0 , означающее непрерывность функции в данной точке.
x→0
Согласно определению теперь мы можем находить производные различных функций. Например,
|
2 ′ |
(x + x)2 − x2 |
2x x + ( x)2 |
|
|
||||||
(x |
) = lim |
|
|
= lim |
|
|
|
= 2x, |
|||
|
|
|
|
|
|||||||
|
|
x→0 |
x |
|
x→0 |
x |
|
|
|
|
|
|
|
sin(x + x)− sin x |
|
|
2sin x cos(x + |
x) |
|||||
(sin x)′ = lim |
= lim |
|
2 |
|
|
2 |
= cos x. |
||||
|
|
|
x |
|
|||||||
|
x→0 |
x |
|
x→0 |
2 |
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь мы использовали первый замечательный предел и свойство непрерывности функции y = cosx , перейдя к пределу под знаком функции. Итак,
′ |
= cosx.Следующую формулу |
(cos x)′ = −sin x получите самостоя- |
(sinx) |
тельно.
Несколько сложнее найти производную логарифмической функции
|
ln(x + |
x) − ln x |
|
|
|
x |
1 |
|
|
|
|
|
|
||||
(ln x)′ = lim |
|
|
x |
|
||||
|
|
= lim ln 1 |
+ |
|
|
= |
||
|
|
|
||||||
x→0 |
x |
x→0 |
|
|
x |
|
|
|
Применим второй замечательный предел в следующей форме
=1 lim ln 1+ x x→0
|
|
|
|
lim 1 |
|
α |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
x |
x |
1 |
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
||||||||
x |
|
|
|
|
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
= |
|
ln(lim |
1 |
+ |
|
|
|
) = |
|
ln lim(1 |
+ α)α |
= |
|
|||||
x |
x |
|
x |
||||||||||||||||
x |
|
x→0 |
|
|
|
|
|
x |
α→0 |
|
|
|
|
||||||
Здесьα = x →0,когда x → 0. x
18.3. Уравнение касательной. Угол между кривыми. Исходя из геометрического смысла производной, можно получить уравнение касательной к кривой в данной точке. Задача сводится к выбору из уравнения
131
пучка прямых y − y0 = k(x − x0 ) конкретного значения углового коэффи-
циента |
k = f ′(x0 ). Таким образом, |
уравнение касательной к графику |
||||
функции |
y = f (x) в точке M0 (x0 , y0 ) |
имеет вид |
|
|||
|
y − y0 = f ′(x0 )(x − x0 ) , |
|||||
а уравнение нормали |
|
|
|
|
|
|
|
y − y |
|
= − |
1 |
(x − x ). |
|
|
0 |
|
||||
|
|
|
f ′(x0 ) |
0 |
||
|
|
|
|
|
||
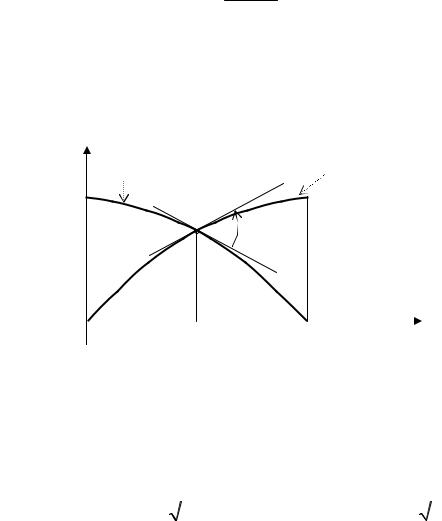
Под углом между кривыми в точке их пересечения естественно понимать наименьший из углов между касательными к кривым в этой точке. Тогда угол может быть вычислен как угол между двумя прямыми с заданными угловыми коэффициентами по формуле
tgϕ = k2 − k1 .
Вкачестве примера найдем, под каким углом пересекаются синусоида
икосинусоида. Задача сводится к нахождению значений производных
функций f1(x) = cos x и f2 (x) = sin x |
при x = π/4 (см. рис. 18.3). |
|
y |
= cos x |
y2 = sin x |
y1 |
||
1 |
|
|
|
|
ϕ ≈ 700 |
x
π π
42
Рис. 18.3
Вычисляем угловые коэффициенты касательных к заданным кривым в точке их пересечения
k |
= f ′(x)| |
|
= −sin(π) = − |
|
2 |
|
, |
k |
|
= f ′(x)| |
|
= cos(π) = |
|
2 |
|
. |
x=π / 4 |
|
|
|
2 |
x=π/ 4 |
|
||||||||||
1 |
1 |
4 |
2 |
|
|
|
2 |
4 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда
132
tgϕ = 
 2
2 2 +
2 + 
 2
2 2 = 2
2 = 2
 2 ϕ ≈ 700 . 1− 0.5
2 ϕ ≈ 700 . 1− 0.5
18.4. Правила дифференцирования. Непосредственное нахождение производных некоторых функций представляет собой трудоемкую задачу. Поэтому выведем правила дифференцирования, которые значительно упростят ее.
Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций
(u(x) + v(x))′ = u′(x) + v′(x) .
Действительно, приращение суммы равно
y = u(x + x) + v(x + x) − u(x) − v(x) = u(x + x) − u(x) + v(x + x) − v(x),
т.е. y = u + |
v.Следовательно, |
|
|
|
|
|
|
|
|
||||
y′ |
y |
= lim |
|
u |
+ |
v |
= lim |
|
u |
+ lim |
|
v |
= u′ + v′, |
= lim |
|
|
|
|
|
|
|
||||||
|
x→0 x |
x→0 |
|
x |
|
x |
x→0 |
|
x |
x→0 |
|
x |
|
так как предел суммы равен сумме пределов и последние пределы существуют в силу предположения о дифференцируемости слагаемых.
Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой функции
(u(x)v(x))′ = u(x)v′(x) + v(x)u′(x). |
(18.1) |
|||||
Действительно, дадим приращение аргументу |
x . Тогда сомножите- |
|||||
ли получат приращения |
u и |
v соответственно и приращение функции |
||||
равно |
|
|
|
|
|
|
y = (u + u)(v + v)− uv = u |
v + v |
u + u |
v. |
|||
Следовательно, |
|
|
|
|
|
|
y′ = lim |
y = v lim u + u lim |
v + lim |
u lim |
v . |
||
x→0 x |
x→0 x |
x→0 x x→0 x x→0 |
|
|||
133
Так как функция v(x) – дифференцируемая, то она непрерывная, поэтому последнее слагаемое в этой формуле равняется нулю и мы приходим к формуле (18.1).
В качестве следствия получим следующее правило: постоянный множитель при дифференцировании выносится за знак производной
(cf (x))′ = cf ′(x) .
Применим это правило для нахождения производной логарифмической функции с произвольным основанием 0, 1
′ |
ln x ′ |
|
1 |
′ |
|
1 |
|
1 |
|
||
(loga x) |
= |
|
|
= |
|
(ln x) |
= |
|
|
|
. |
|
lna |
lna |
|
||||||||
|
lna |
|
|
|
|
x |
|||||
Производная частного вычисляется по следующей формуле:
|
|
′ |
|
′ |
|
′ |
u |
= |
u v − v u |
||||
|
|
|
|
|
|
|
|
|
v |
2 |
|||
v |
|
|
|
|||
при условии, что знаменатель в данной точке не обращается в ноль. Действительно, выразим приращение частного через приращения делимого и делителя
|
|
|
|
|
|
|
|
u + u |
|
u |
v u − u |
v |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
y = |
|
|
|
− |
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
v + v |
v |
v(v + v) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
v lim |
u − u lim |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда lim |
y = |
|
x→0 |
x |
|
x→0 |
x |
= |
u′v − v′u |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim v(v + v) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x→0 |
x |
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдём, например, производную функции y = tgx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
sin x |
′ |
|
|
′ |
|
|
|
|
|
′ |
|
sin |
2 |
x + cos |
2 |
x |
|
1 |
|
|
||||||||
|
|
|
|
(sin x) cos x − (cosx) sin x |
|
|
|
|
|
|
||||||||||||||||||||
(tg x)′ = |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
. |
||
|
|
|
|
cos |
2 |
(x) |
|
|
|
|
cos |
2 |
x |
|
|
cos |
2 |
|
||||||||||||
|
|
cosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||
Получите самостоятельно производную функции y = ctg x .
134

Лекция 19. Производная (продолжение)
19.1. Дифференцирование сложной и обратной функций. Часто приходится находить производную так называемой сложной функции, представляющей собой «функцию от функции». Например,

 x2 +1, sin(2x + 3), e− x2
x2 +1, sin(2x + 3), e− x2
или в общем виде
y = f (ϕ(x)) = F(x).
Эта функция представлена как суперпозиция (композиция)двух функций
y = f (u), u = u(x),
где «внешняя» функция f (u) – дифференцируемая функция промежуточной переменной u, а «внутренняя» функция u(x) – дифференцируемая функция независимой переменной x. Оказывается, что производная сложной функции по независимой переменной равна произведению производной функции по промежуточной переменной на производную промежуточной переменной по независимой переменной
y′x = fu′(u(x))u′(x).
Это так называемое цепное правило доказывается следующим образом. Используя определение производной, получим
y′ |
= lim |
y = lim |
y lim |
u . |
|
x |
x→0 |
x |
x→0 |
u x→0 |
x |
|
|||||
В силу непрерывности функции |
u(x) из условия |
x → 0 следует, что |
|||
u → 0. Отсюда вытекает указанная формула в предположении, что |
|||||
u ≠ 0. |
u =u(x+ |
x)−u(x) =0, т.е. u(x+ x) =u(x)то |
|||
Если же окажется, что |
|||||
y = f (u(x+ x))− f (u(x)) =0 . Значит, |
′ |
′ |
|
||
u(x)=0и y(x)=0и формула диф- |
|||||
ференцирования сложной функции |
0 = fu′(u(x)) 0справедлива и в этом |
||||
случае. Далее, многие элементарные функции определены как обратные функции к другим функциям, например, y = arcsin x , y = ln x.
Возникает вопрос: нельзя ли найти производную обратной функции, зная производную исходной функции? Оказывается, можно. А именно, если для функции y = f (x)(например, для y = arcsin x ) существует обратная
135

функция x = ϕ(y) ( x = sin y , −π/2 ≤ y точке y имеет производную ϕ′(y) ≠ 0 ответствующей точке x функция y = мую по правилу
f ′(x) = |
1 |
, |
|
||
|
ϕ′(y) |
|
≤ π/2), которая в рассматриваемой (в нашем примере, cos y ), то в со- f (x) имеет производную, вычисляе-
(19.1)
в котором y = f (x). В нашем примере |
|
|
|
|
|
|
|
|
||||
(arcsin x)′ = |
1 |
= |
1 |
= |
1 |
|
= |
1 |
|
, |
||
(sin y)′ |
|
|
|
|
|
|
|
|||||
|
+ 1− sin2 y |
1− x2 |
||||||||||
|
|
cos y |
|
|
|
|
||||||
где знак « + » взят в силу того, что в промежутке −π/2 ≤ y ≤ π/2, в котором обратная функция существует, cos y положителен.
Для доказательства формулы (19.1) продифференцируем равенство x = ϕ(y) по переменной x, применяя правило дифференцирования сложной
функции (считая y функцией x): |
|
|
|
1= x' |
y' |
, |
|
y |
|
x |
|
откуда следует |
|
|
|
y′x = |
1 |
. |
|
|
|
||
x′ |
|
||
|
y |
|
|
Геометрический смысл этой формулы виден из рис. 19.1
yx = ϕ(y)
y |
y = f (x) |
β |
|
α |
x |
x |
|
Рис. 19.1 |
|
Касательная к кривой y = f (x) образует с положительным направле- |
|
нием оси Ox угол α . Касательная к той же кривой |
x = ϕ(y) образует |
угол β с положительным направлением оси Oy . Согласно геометриче-
′ |
′ |
α и β |
скому смыслу производной f (x) = tgα |
и ϕ (y) = tgβ. Но углы |
|
136 |
|
|
дополняют друг друга доπ/2, поэтому tgα tgβ =1. Это соотношение и выражает формулу дифференцирования обратной функции.
Найдём производную показательной функции y = ax , a > 0. Обратная для неё функция x = loga y . Применяя формулу (19.1)имеем
|
(ax )′ = |
1 |
|
= |
|
1 |
|
|
|
= ylna = ax lna |
|
|
|
(loga y)′ |
|
1 |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
lna y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Применяя это правило, найдите самостоятельно производные функций |
||||||||||||
|
|
|
arccos x , arctgx . |
|
|
|||||||
Применим |
формулу |
производной |
показательной |
функции |
||||||||
(ax )′ = ax ln a для вывода производной степенной функции |
|
|||||||||||
(xα )′ = (eαln x )′ = eαln xα 1 = αxα−1. x
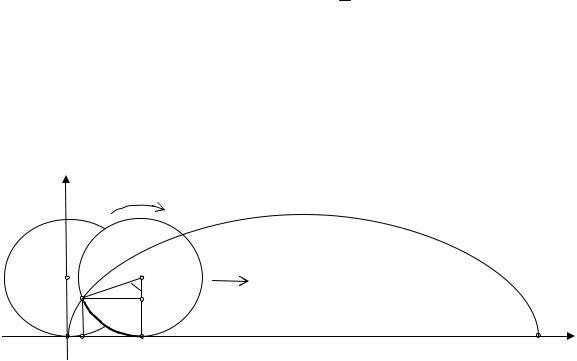
19.2.Дифференцированиефункций, заданных параметрически. Касательная к параметрически заданной кривой. Получим теперь правило нахождения производной параметрически заданной функции. Такая функция, например, возникает в задаче о траектории фиксированной точки M окружности радиуса r , катящейся без скольжения по осиOx.
|
|
C |
OP = MP = rt |
|
|
r |
x = OP − NP = rt − rsint |
||
t |
||||
M |
|
|
||
|
K |
y = r − KC = r − r cost |
||
|
|
|||
|
|
|
x |
|
O N |
|
P |
2πr |
|
|
|
|
||
|
|
|
Рис. 19.2 |
Пусть в начальный момент точка M находится в начале координат. В качестве параметра возьмем угол t , на который повернется радиус окружности O1O , приняв положение CM. Выразим координаты точки M(x, y) как функции параметра t . Из рисунка видно, что длина дуги MP равна
137

длине отрезка OP и равна rt . Следовательно, из треугольника MKC найдём
x = r(t − sint) |
≤ t ≤ 2π. |
|
|
0 |
|
y = r(1 |
− cost) |
|
Выбранные границы изменения параметра соответствуют одному обороту окружности. Таким образом, мы получили зависимость переменной y от переменной x, выраженную не явно, а через промежуточный параметр t . График этой зависимости представлен на рис. 19.2, а кривая называется циклоидой. Название циклоида означает: «напоминающая о кру-
ге». Его дал Галилео Галилей (1564–1642).Конечно, можно связать |
x и |
y непосредственно, исключив параметр t . Однако эта функция |
будет |
иметь достаточно сложный вид, поэтому возникает необходимость в нахождении производной y как функции переменной xна основе параметрического задания функции.
Рассмотрим задачу в общем виде. Пусть функция y = f (x) задана параметрически
x = ϕ(t) |
, |
α ≤ t ≤ β, |
|
|
|
|||
|
|
|
|
|
||||
y =ψ (t) |
|
|
|
|
|
|
|
|
где функции ϕ(t) |
и ψ(t)– дифференцируемы и функция ϕ(t) имеет об- |
|||||||
ратную. Тогда по определению производной имеем |
||||||||
|
|
y = |
lim |
y |
lim |
y |
= ψ′t . |
|
y′ |
= lim |
x→0 |
t |
= |
t→0 |
t |
||
|
|
|
|
|||||
x |
x→0 |
x |
|
x |
|
x |
ϕ′ |
|
|
lim |
lim |
||||||
|
|
|
|
|
|
t |
||
|
|
|
x→0 |
t |
t→0 |
t |
|
|
Здесь мы использовали то, что в силу непрерывности обратной функции к ϕ(t) из x → 0 следует t → 0.
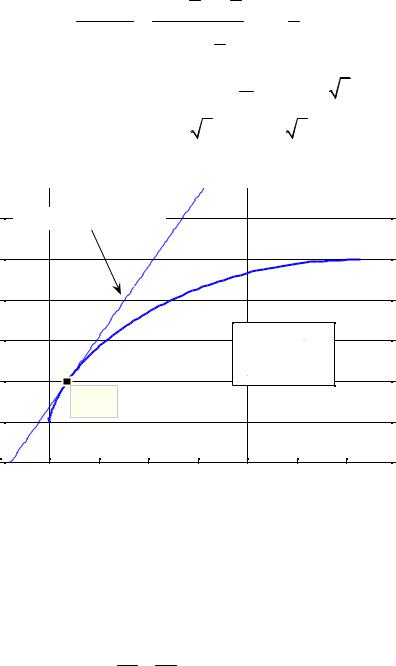
Задача. Получить уравнение касательной к циклоиде. Пусть окружность радиуса r =1совершила одну шестую часть оборота. Найдем уравнение касательной в соответствующей точке траектории. Одна шестая часть оборота окружности соответствует значению параметра t0 = π/3, а
|
|
|
|
|
|
|
координаты |
точки: |
x0 = x(t0 ) = (t − sint) |
|
t=π /3 = π/3− 3/2, |
||
|
|
|
||||
y0 = y(t0 ) =1− cost t=π/3 = 0,5. Производную y′x находим как производную функции заданной параметрически
138
|
|
|
|
2sin t |
|
cos t |
|
|
|
||
|
y′ |
= |
sint |
= |
2 |
|
2 = ctg t |
|
|
||
|
x |
1 |
− cost |
|
2sin |
2 |
t |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
В данной точке циклоиды она равна |
y′ |
= ctg t0 = ctg π = |
3 . Поэтому |
||||||||
|
|
|
|
|
x |
|
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение касательной в этой точке y = |
3x + 2 − π/ |
3 (см. рис.19.2). |
|||||||||
2.5 |
y=sqrt3*x+2-pi/sqrt3 |
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
x = t - sint |
|
|
|
|
|
|
|
|
|
|
|
y =1 - cost |
|
|
|
0.5 |
|
|
|
|
|
|
|
0 < t < pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 0.18 |
|
|
|
|
|
|
|
|
|
|
|
Y: 0.498 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
0 |
|
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
||
Рис. 19.3
19.3. Производная функции, заданной неявно. Касательная к неявно заданной кривой. Рассмотрим случай, когда функция задана неявно. Пример такой функции y = f (x) дается уравнением
x2 + y2 =1( y > 0). a2 b2
Графиком этой функции служит верхняя половина эллипса. Покажем, как находить производную этой функции, не выражая явно y через x (для некоторых неявно заданных функций такое вообще невозможно). Продифференцируем это уравнением по переменной x , считая, что переменная y является функцией x
1 |
2x + |
1 |
2yy′ = 0 |
y′ = − |
b2x |
|
a2 |
b2 |
a2 y |
||||
|
|
|
||||
|
|
|
139 |
|
|
|
В общем случае неявно заданной функции нужно действовать анало- |
|||||||||||||||||||
гичным образом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
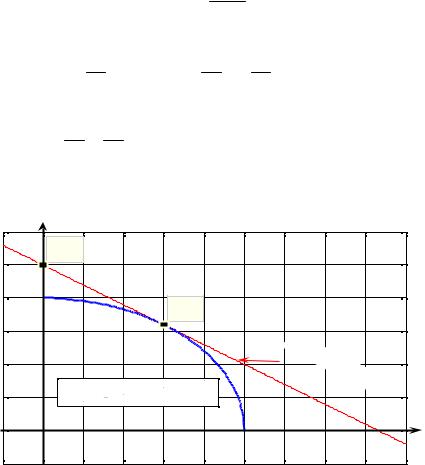
Задача. Получить уравнение касательной к эллипсу в точке |
M0 (x0 , y0 ) |
|||||||||||||||||||
.Уравнение касательной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y − y |
|
= − b2 x0 (x − x |
|
) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
a2 y |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
после умножения на |
y0 примет вид x0 x + y0 |
y = 1. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
b2 |
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
Для эллипса |
|
x2 |
+ y2 |
=1 |
в точке |
M |
0 |
(3,1.6) |
|
|
уравнение касатель- |
||||||||
|
|
|
25 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ной |
3x +10y − 25 = 0 |
(см. рис.19.4). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y: 2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
X: 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Y: 1.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
5= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
|
0.5 |
|
1/25x + 1/4y |
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
2 |
|
3 |
|
4 |
5 |
|
6 |
|
|
|
7 |
|
8 |
9 |
|
|
|
|
|
|
|
|
|
|
Рис. 19.4 |
|
|
|
|
|
|
|
|
|
|
|
|
19.4. Логарифмическое дифференцирование. Применим метод нахождения производной неявно заданной функции к выводу производной показательно-степенной функции вида
y = u(x)v(x) .
Прологарифмируем обе части этого равенства, опуская для краткости аргумент
ln y = vlnu.
Найдем теперь y′(x) как производную неявно заданной функции
140
