
9278
.pdf
180
направлению к сопротивлению R0, на которое замкнуты стержни. Показать, что мощность индукционного тока в контуре ABR0 равна мощности сил, которые надо приложить к проводнику AB, чтобы он двигался равномерно вверх.
Дано: Решение.
IПроводник AB движется в магнитном
a |
поле напряженностью H, создаваемым |
b |
током I. Поскольку площадь контура |
a<b |
ABR0 при этом уменьшается, возникает |
R0 |
изменение магнитного потока через |
|
замкнутый контур. |
|
|
P=Pi |
|
В результате в контуре ABR0 возникнет ЭДС. индукции и потечет индукционный ток Ii. Таким образом, на проводник с током AB, находящийся в магнитном поле прямого тока I будет действовать сила Ампера.
Магнитное поле прямого тока может быть вычислено по выражению:
H = I . 2π R
Согласно правилу левой руки, сила Ампера, действующая на проводник AB, направлена против скорости движения контура. Величина силы Ампера определяется выражением:
R |
b |
R |
R |
|
R |
b |
R |
|
Ii I |
|
b |
|
|
|
|
|
|
|
|
||||||||
FA |
= μ0 Ii H ´ dl |
|
= - j |
× μ0 Ii H × dx = - - j |
× μ0 |
ln |
, |
||||||
2π |
|
||||||||||||
|
a |
|
|
|
|
a |
|
|
|
a |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
где Ii - индукционный ток, возникающий в контуре ABR0, H - напряженность магнитного поля, создаваемого током I, вектор FÜ направлен вдоль тока Ii.
Для того, чтобы проводник AB двигался равномерно со скоростью υ , действующая сила Ампера должна быть уравновешена некоторой механической силой ; = ;Ë, направленной в сторону движения проводника (вверх).
Мощность силы Ампера может быть вычислена как:
P = F ×υ = μ0 Ii I ×V |
ln |
b |
. |
|
|
||||
A |
2π |
|
a |
|
|
|
|
|
|
Найдем величину индукционного тока Ii, текущего в контуре. Из закона Ома следует:
181
•E = ßE~ .
Сдругой стороны, вследствие изменения магнитного потока возникает
электродвижущая сила
•E = − FΦF .
Найдем магнитный поток через контур:
|
|
Ф= |
R R |
μ I |
|
dS |
|
|
|
|
|||||||||||
|
|
BdS = |
0 |
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
S (t ) |
|
|
|
|
|
2π |
S (t ) |
R |
|
|
|
|
|||||
Определим элемент площади в виде: F = F Fë. Следовательно, магнитный поток |
|||||||||||||||||||||
|
Ф = μ0 I dy × dx = μ0 I × y (t )× ln b . |
||||||||||||||||||||
|
|
|
|
y (t) b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 a |
R |
|
2π |
|
|
|
a |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Зная магнитный поток, можно найти ЭДС как |
|
|
|
|
|
|
|
|
|
||||||||||||
Ei |
= - |
d F |
= μ0 I |
× ln |
b |
× |
dy (t ) |
= μ0 I × ln |
b |
×υ , |
|||||||||||
|
|
|
|
||||||||||||||||||
|
|
dt 2π |
|
a |
dt |
|
|
|
2π |
|
a |
||||||||||
где υ – скорость движения проводника AB.
Используя закон Ома, вычислим значение индуцированного тока в контуре:
Ik |
= - μ0 I |
ln |
b |
×V . |
|
||||
|
2π |
|
a |
|
С учетом вычисленного значения индукционного тока, выражение для его мощности согласно закону Джоуля-Ленца имеет вид:
2 |
|
|
μ02 I 2υ2 |
|
b |
2 |
μ02 I 2υ2 |
b |
2 |
||||||||
Pi = Ii |
R0 |
= |
|
|
|
ln |
|
|
× R0 = |
|
|
|
|
ln |
|
. |
|
(2π R |
) |
2 |
|
(2π ) |
2 |
R |
|
|
|||||||||
|
|
|
|
|
a |
|
|
0 |
|
a |
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С другой стороны, мощность механической силы, действующей на контур:
2 |
2 |
2 |
|
|
b 2 |
|
|
|
|
|
|
|
|
||
|
μ0 |
I υ |
|
ln |
|
|
|
|
2 2 2 |
|
b |
2 |
|||
|
|
|
|
||||||||||||
P = |
|
|
|
|
|
a |
= |
μ0 I |
υ |
|
|||||
|
|
|
|
|
|
|
|
|
|
ln |
|
. |
|||
2π × 2π × |
R0 |
(2π ) |
2 |
|
|
||||||||||
|
|
|
R |
|
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Таким образом, P=Pi, что и требовалось доказать.
Ответ: P=Pi.
182
Задачи для самостоятельного решения
1.В однородное магнитное поле напряженностью 100 кА/м помещена квадратная рамка со стороной 10 см. Плоскость рамки составляет с направлением магнитного поля угол α = 60°. Определить магнитный поток, пронизывающий рамку.
2.В одной плоскости с бесконечным прямолинейным проводом с током 20 А расположена квадратная рамка со стороной, длина которой 20 см, причем две стороны рамки параллельны проводу, а расстояние от провода до ближайшей стороны рамки равно 5 см. Определить магнитный поток, пронизывающий рамку.
3.Кольцо из алюминиевого провода помещено в магнитное поле перпендикулярно линиям магнитной индукции. Диаметр кольца 30 см, диаметр провода 2 мм. Определить скорость изменения магнитного поля, если ток в кольце 1 А.
4.Круговой проволочный виток площадью 10 см2 находится в однородном магнитном поле, индукция которого 0,8 Тл. Плоскость витка перпендикулярна к направлению магнитного поля. Найти среднюю ЭДС индукции, возникающую в
витке при выключении поля в течение времени 15 мс.
5. В магнитное поле, изменяющееся по закону ( ) = 0,5cos(4 ), помещена квадратная рамка со стороной 80 см, причем нормаль к рамке образует с направлением поля угол α = 30°. Определить ЭДС индукции, возникающую в рамке в момент времени 5 с.
6. Стержень длиной 70 см вращается с частотой 2 с-1 вокруг оси, проходящей через его конец и перпендикулярной к направлению однородного магнитного поля с индукцией 0,1 Тл. Определить возникающую на концах стержня ЭДС индукции.
7. Горизонтальный стержень длиной 1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельна магнитному полю, индукция которого 5 мТл. При какой частоте вращения стержня разность потенциалов на концах этого стержня будет составлять 1 мВ?
8. В однородном магнитном поле равномерно вращается прямоугольная рамка с частотой 600 мин-1. Амплитуда индуцируемой в рамке ЭДС составляет 3 В. Определить максимальный магнитный поток через рамку.
183
9. Плоскость проволочного витка площадью 100 см2 и сопротивлением 5 Ом, находящегося в однородном магнитном поле напряженностью 50 кА/м, перпендикулярна линиям магнитной индукции. При повороте витка в магнитном поле, заряд, прошедший по витку, составляет 20 мкКл. Определить угол поворота витка.
10. В однородное магнитное поле с индукцией 0,3 Тл, помещена прямоугольная рамка с подвижной стороной, длина которой 15 см. Определить ЭДС индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиям магнитной индукции со скоростью 10 см/с.
КОЛЕБАНИЯ И ВОЛНЫ
§ 1. Классификация колебаний
Колебательным процессом, или колебанием называют любой периодический (т.е.
повторяющийся процесс)
x(t)= x(t+nT) |
(1.1) |
где t - время, T - период колебания, n = 1, 2, ..., x – отклонение некоторой величины от своего равновесного значения. Выражение (1.1) означает, что значение величины x повторяется через промежутки времени T, 2T, и т.д. Иногда равенство (1.1) приближенное, например, если колебания затухают. Колебательные процессы окружают нас повсюду, и такой вид движения относится к самым распространенным в природе и технике. Колебания существуют не только в физических системах; это может быть биологический объект, экономический или социальный процесс и т.п. Мы будем рассматривать физические системы, хотя используемое математические описание, известное как теория колебаний, является весьма общим.
Колебания возникают в любой системе, имеющей устойчивое состояние равновесия при отклонении от этого состояния. В механических колебательных системах при отклонении от равновесия возникает сила, которая стремится
184
вернуть систему назад; её называют возвращающей или квазиупругой силой.
Например, в случае самой простой модели - груз на пружине - это сила упругости. Слово «сила» в общем случае не следует понимать буквально: в механике это может быть и момент силы, для электромагнитных колебаний эта «сила» обусловлена явлением самоиндукции.
Колебания различаются по нескольким классификационным признакам:
1. По форме (т.е по виду функции x(t)): гармонические и негармонические (все
остальные). Гармоническими называют колебания, |
описываемые функцией времени |
|
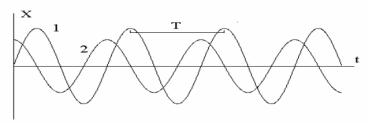
вида (см. рис.1): |
( ) = sin(U + ), |
|
где A - амплитуда (максимальное отклонение), ω - циклическая частота, φ0 - начальная фаза колебаний.
Рис.1 Осциллограммы гармонических колебаний. Начальная фаза 1-го колебания равна нулю, второго - π/2.
Гармонические колебания выделяются из всех других по следующим двум причинам: во-первых, достаточно малые колебания, как правило, являются гармонически. Во-вторых, колебания любой другой формы (негармонические), в сущности, представляют собой суперпозицию гармонических (в математике это положение называется теоремой Фурье, а соответствующее представление периодических функций - рядом Фурье).
2. По характеру возникновения колебания делятся на собственные (или свободные) и
вынужденные. Собственные - это колебания, вызванные только начальными условиями (например, начальным смещением или начальной скоростью).
Вынужденные - это колебания, вызванные действием периодической (т.е. также
колебательной) внешней «силы».
185
2. По динамике процесса колебания делятся на незатухающие, затухающие (при этом амплитуда уменьшается со временем), нарастающие (амплитуда растет). Например, собственные колебания всегда являются затухающими. Существуют также автоколебания - колебания, вызванные действием непериодической «силы» и параметрические колебания - колебания, вызванные периодическим изменением какого-либо параметра системы, связанного с его энергией (например, раскачивание качелей без внешнего воздействия).
§2. Кинематика гармонических колебаний
Рассмотрим гармоническое колебание, описываемое уравнением: |
|
( ) = sin(U + ). |
(2.1) |
Напомним, что x(t) - смещение некоторой величины от равновесного состояния.
Колебание определяется заданием амплитуды, частоты и начальной фазы. Поскольку |
|
период функции sint равен 2π, период функции sinU = sin !™y |
будет равен T . |
Поэтому период, частота ν, циклическая частота ω связаны соотношением: |
|
£ = y , U = 2—£. |
(2.2) |
Если смещение определяется формулой (2.1), то мгновенная скорость υ есть производная по времени от x, а ускорение a – вторая производная:
( ) = ′( ) = U(z |(U + ), |
|
( ) = J( ) = − U! sin(U + ). |
(2.3) |
Заметим, что последнюю формулу можно записать в виде: |
|
( ) = JJ(+) = −U! ( ). |
(2.4) |
Из выражений (2.3) ясно, что максимальная скорость и максимальное ускорение
определяются формулами †l = U, †l = U!. |
(2.5) |
186
§3. Гармонический осциллятор, начальные условия
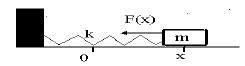
Рассмотрим простейшую модель колебательной системы – груз массы m, закрепленный на пружине с коэффициентом жесткости k, который может перемещаться без трения в горизонтальном направлении (рис.2).
Рис.2. Колебания груза на пружине
В произвольный момент времени t на него действует сила упругости, и второй закон
Ньютона для груза имеет вид: |
< = < JJ = −: ( ). |
|
|
(3.1) |
|
Разделим выражение (3.1) на массу m и запишем его в форме: |
|
|
|
JJ + U! = 0, |
(3.2) |
где U! = :⁄<. Пока это только обозначение, и смысл величины ω0 предстоит выяснить.
Мы получили дифференциальное уравнение, связывающее смещение и его вторую производную. Подставив выражение (2.4) для ускорения в формулу (3.2) мы получаем тождество (т.е. равенство (3.2) выполняется в любой момент времени при U = U ). Это означает, что общим решением дифференциального уравнения (3.2)
является гармоническое колебание, циклическая частота которого равна: |
|
U = ì:⁄<. |
(3.3) |
Дифференциальное уравнение (3.2) называется уравнением гармонического осциллятора (oscillation - колебание). Оно имеет универсальный вид для любой системы, где возможны незатухающие гармонические колебания. Итак, частота собственных колебаний пружинного маятника определяется формулой (3.3), а в общем случае она определяется свойствами самой колебательной системы.
Выясним, от чего зависит амплитуда и начальная фаза. Положив в формуле (2.1) и в первой формуле (2.3) t = 0, запишем:
187
= (0) = sin , = (0) = U cos .
Отсюда можно выразить амплитуду и начальную фазу (возвести в квадрат и сложить, избавимся от тригонометрических функций):
! = ! + !sU!, = ( -(í‘•• •). |
(3.4) |
Таким образом, амплитуда и начальная фаза собственных колебаний определяется начальными условиями. В рассмотренном примере это начальное смещение груза и начальная скорость. В частности, если колебание возникает из-за начального смещения (начальная скорость равна нулю), то как видно из (3.4), A= x0, φ0=π/2. Если
колебание вызвано начальным толчком (заданием начальной скорости в положении
= ‘• , = 0
равновесия), то í• .
§4. Преобразование энергии в процессе гармонических колебаний
При любом колебательном процессе происходит периодическое преобразование энергии из одного вида в другой. В рассмотренной модели — это потенциальная энергия деформированной пружины и кинетическая энергия груза. Они
определяются выражениями:
Ñq = :2! = 12 : !sin!(U + ),
ÑŽ = <2 ! = 12 <U! !cos!(U + ).
Поскольку : = <U!, коэффициенты перед sin!(U + ) и cos!(U + )
одинаковы. Складывая эти формулы (и учтя основное тригонометрическое тождество
|ª{!B + (z|!B = 1, B = U! + ), получим:
Ñq + ÑŽ = <U! ! = const. (4.1)
!

188
Рис.3. Преобразования энергии при гармонических колебаниях
Таким образом, хотя потенциальная и кинетическая энергии изменяются со временем
(рис.3), полная энергия колебаний не зависит от времени и определяется выражением (4.1). Видно, что максимум кинетической энергии соответствует минимуму потенциальной и наоборот, а их сумма остается постоянной. Сохранение энергии обусловлено тем, что мы пока не учли трение. Хотя формула (4.1) получена для простейшей модели колебательного движения, заметим, что энергия колебаний в любой системе пропорциональна квадрату амплитуды и квадрату частоты.
§5. Физический маятник
Физический маятник - это любое тело, имеющее ось вращения, не совпадающую с его центром масс (например, рис.4).
Рис.4. Физический маятник. Здесь точка С - центр масс, l - его расстояние до оси вращения О.
При выведении из состояния равновесия он будет совершать колебания, которые при
небольших амплитудах будут гармоническими. Покажем это. Исходим из основного |
|
уравнения динамики вращательного движения: |
K = NC, |

189
где J - момент инерции, M - момент сил, β - угловое ускорение. Из рис.4 ясно, что
вращающий момент создает только сила тяжести, поэтому его можно записать:
K = −<-ÜsinB,
где α - текущий угол отклонения, зависящий от времени. Поскольку угловое ускорение ω есть вторая производная от α, подставив все в (12), и приводя к виду уравнения осциллятора, запишем:
BJJ + îDE†*Ïu = 0. |
(5.1) |
Обозначив †*Ïî = U!, мы получим дифференциальное |
уравнение «похожее» на |
уравнение гармонического осциллятора (3.2). Конечно, это совсем другое уравнение и гармоническое колебание не является его решением, а значит колебания физического маятника не являются в общем случае гармоническими. Однако, если они достаточно малы, так, что можно считать |ª{B ≈ B, то уравнение (5.1)
превратится в (3.2) (разумеется для текущего значения угла α(t)), где циклическая
частота собственных колебаний определяется формулой:
U = !™y = 2—¢†*Ïî .
Следовательно, период колебаний равен:
t = !™ = 2—¢ î .
í• †*Ï (5.2)
В частности, для математического маятника, момент инерции которого определяется как N = <Ü!, из выражения (5.2) получается хорошо знакомая вам формула:
t = 2—ï-Ü .
Для пружинного маятника период можно найти, учитывая зависимость ω от k.
