
книги / Численные методы решения задач строительства. Ч. 1
.pdf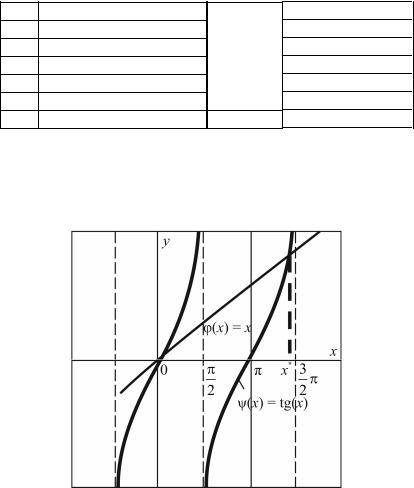
Таблица 2 . 2 . Таблица табулирования
хf(x) = х – tg(x)
0 |
0,000 |
0,5 |
–0,046 |
1 |
–0,557 |
1,5 |
–12,601 |
2 |
4,185 |
2,5 |
3,247 |
хf(x) = х – tg(x)
3 |
3,143 |
3,5 |
3,125 |
4 |
2,842 |
4,5 |
–0,137 |
5 |
8,381 |
Вдействительности на этом участке функция f(x) = х –
–tg(x) терпит разрыв (т.е. не выполняются условия теоремы 2.1), и это хорошо видно на рис. 2.4.
Рис. 2.4. Локализация корней уравнения х – tg(x) = 0
Таким образом, искомый корень уравнения находится на отрезке [4, 4,5], где выполняются условия теоремы 2.1.
31

2.2. Второй этап. Уточнение корня
Iteration (итерация) – повто-
рение, результат повторного применения какой-либо математической операции.
Этап уточнения корня заключается в построении по-
следовательности приближенных значений (итераций)
корня уравнения (2.1) исходя из начального приближения корня x0 (нулевой итерации).
Эта последовательность
x0, x1, x2,……xn…. (2.4)
называется итерационной последовательностью.
Если существует предел этой последовательности, т.е.
lim x x* , |
(2.5) |
n n
то говорят, что итерационный процесс (2.4) сходится и схо-
дится к точному решению уравнения x* [2].
На практике итерационный процесс ограничивают конечным числом шагов (итераций) n. Количество итераций зависит от требуемой точности нахождения корня.
Для прекращения итерационного процесса применяются различные критерии, зависящие от вида функции
y = f(x) в окрестности корня. |
y |
||||||
1. Если функция |
достаточно |
||||||
«пологая», то итерационный про- |
|
|
|
||||
цесс продолжается до тех пор, пока |
|
|
|
||||
две соседние итерации не станут |
|
|
|
||||
достаточно близкими, т.е. пока не |
|
|
|
||||
выполнитсяусловие |
|
|
|
x |
|||
|
|
|
|||||
|
xn 1 xn |
|
. |
(2.6) |
|
|
|
|
|
|
|
|
|||
32
2. Если функция у = f(x) «кру- |
y |
|||||||
то» меняет свои значения, целесо- |
|
|
|
|
||||
образно использовать условие |
|
|
|
|
||||
|
f xn |
|
. |
(2.7) |
|
|
|
|
|
|
|
|
|
|
|||
Если условие (2.6) или (2.7) |
|
|
|
|
||||
выполняется, то в качестве при- |
|
|
|
x |
||||
|
|
|||||||
ближенного решения |
уравнения |
|
|
|
|
|||
(2.1) с заданной точностью принимают n-ю итерацию, т.е.
x* xn .
Если ни одно из этих условий не выполняется, то итерационный процесс необходимо продолжить.
Рассмотрим несколько итерационных (приближенных) методов решения нелинейных уравнений. Выбор того или иного метода зависит от вида функции y = f(x).
2.2.1. Метод половинного деления (бисекции)
Пусть функция y = f(x) удовлетворяет условиям теоремы 2.1 на отрезке [a, b], т.е. уравнение (2.1) имеет единственный корень на этом отрезке.
Рис. 2.5. Схема метода бисекции
33
Метод половинного деления (бисекции) это один из простейших методов решения нелинейных уравнений. Приводим алгоритм и геометрическую интерпретацию (рис. 2.5) этого метода.
Алгоритм метода бисекции
1. Делим отрезок [a, b] пополам.
|
2. |
Если |
f a b |
|
0, |
то x* a b |
является |
корнем |
||
|
|
|
|
2 |
|
|
2 |
|
|
|
уравнения (2.1). |
|
|
|
|
|
|
|
|||
|
3. |
Если |
a b |
|
0, |
|
|
a b |
||
|
f |
2 |
|
то из двух отрезков a; |
2 |
, |
||||
|
|
|
|
|
|
|
|
|
||
a b |
|
|
|
|
|
|
|
|
|
|
|
2 |
;b выбираем тот, на концах которого функция f(x) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
имеет разные знаки.
4.Новый «суженный» отрезок [a1, b1] снова делим пополам и проводим тот же анализ и т.д.
5.В результате получаем на каком-то этапе или точ-
ный корень уравнения (2.1), или же бесконечную последо-
вательность вложенных друг в друга отрезков,
|
[a1, b1], [a2, b2], …………………[an, bn] |
|
||
таких, что |
f(ai) f(bi) < 0, (i = 1, 2, …..) |
(2.8) |
||
и |
b a |
1 |
(b a). |
(2.9) |
|
||||
|
i i |
2n |
|
|
Левые концы a1, a2, ..., an,… и правые концы b1, b2, ..., bn,… этих отрезков образуют монотонные последовательности – соответственно неубывающую и невозрастающую.
Доказывается утверждение, что существует общий предел x*, который является корнем уравнения (2.1).
x* lim a |
lim b . |
(2.10) |
||
n |
n |
n |
n |
|
|
|
|
||
34

Метод половинного деления легко реализуется на ЭВМ по следующей схеме.
Для нахождения приближенного значения корня урав-
нения (2.1) с заданной точностью необходимо циклически повторить следующую последовательность действий:
1) отрезок [a, b] делим пополам x a 2 b ;
2) если | f(x)| > ε, переходим на пункт 3, иначе – на пункт 5;
3)если f(x)·f(b) ≤ 0, то принимаем a = x, иначе b = х. То есть из двух отрезков выбираем тот, на концах которого функция имеет разные знаки, и новый «суженный» отрезок вновь называем отрезком [a, b];
4)если |a – b| > ε, то выполняется пункт 1, иначе – пункт 5;
5)в качестве приближенного решения уравнения (2.1)
сзаданной точностью ε принимается x a 2 b .
Замечание. Метод половинного деления практически удобно применять для грубого нахождения корня заданного уравнения, поскольку при увеличении точности объем вычислительной работы значительно возрастает.
2.2.2. Метод хорд
Пусть функция y = f(x) на отрезке [a, b] удовлетворяет условиям теорем 2.1, т.е. уравнение f(x) = 0 имеет на этом отрезке единственный корень x*.
Положим для определенности f ″(x) > 0 (рис. 2.6). Вместо деления отрезка пополам разделим его в отноше-
нии f(a): f(b).
С геометрической точки зрения способ пропорцио-
нальных частей эквивалентен замене кривой y = f(x) хордой, проходящей через точки A[a, f(a)] и B[b, f(b)].
35
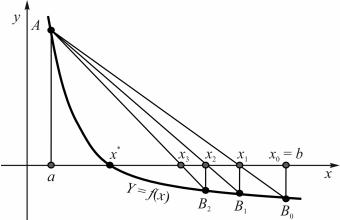
Рис. 2.6. Схема метода хорд (1-й случай)
Для построения итерационной последовательности по методу хорд необходимо выбрать начальное приближение
(нулевую итерацию) х0.
Если функция y = f(x) имеет 2-ю производную, сохра-
няющую знак на этом отрезке, то начальное приближение х0 выбирается исходя из условия
f(x0) f ″(x0) < 0. |
(2.11) |
Рассмотрим два случая, каждый из которых определен видом функции y = f(x) на отрезке [a, b].
Первый случай. Полагаем f(а) > 0, f(b) < 0 и f ″(x) > 0
для x [a, b] (рис. 2.6).
1.В качестве нулевого приближения корня выбираем тот конец отрезка [a, b], для которого выполняется условие (2.11), т.е. выбираем правый конец отрезка [a, b], х0 = b.
2.Проводим хорду АВ0 и за первое приближение (первую итерацию) х1 принимаем абсциссу точки пересечения хорды с осью ОХ.
3.Второе приближение х2 получаем как абсциссу точки пересечения хорды АВ1 с осью ОХ.
36

4. Аналогичным образом строим итерационную последовательность
х0 = b, x1, x2,……., xn,….
В математическом анализе доказывается теорема, что эта итерационная последовательность сходится к корню уравнения х* (2.1).
Для получения формулы (n + 1)-й итерации хn+1 запишем уравнение хорды ABn:
x xn |
|
y f (xn ) |
(2.12) |
|||
|
|
|
|
. |
||
x |
a |
f x |
f (a) |
|||
n |
|
|
n |
|
|
|
Полагая х = xn+1 и y = 0, найдем абсциссу точки пересечения хорды ABn с осью ОХ, т.е. (n + 1)-ю итерацию хn+1.
Вэтом случае левый конец отрезка [a, b] неподвижен,
ипоследовательные приближения (итерации) определяются по формуле
x0 b; |
xn 1 |
xn |
f (xn ) |
|
(xn a). |
(2.13) |
|
f (xn ) f |
(a) |
||||||
|
|
|
|
|
Второй случай. Полагаем f(а) < 0, f(b) > 0 и f ″(x) > 0
для x [a, b] (рис. 2.7).
Рис. 2.7. Схема метода хорд (2-й случай)
37

В качестве нулевого приближения корня выбираем тот конец отрезка [a, b], для которого справедливо усло-
вие (2.11).
Для данного случая выбирается левый конец отрезка [a, b], т.е. х0 = а, а в качестве неподвижного конца х = b.
Аналогично первому случаю строим последовательность приближений, сходящуюся к точному решению х* уравнения (2.1) и определяемую следующим соотношением:
x0 a; |
xn 1 xn |
f (xn ) |
(b xn ). |
(2.14) |
|
f (b) f (xn ) |
|||||
|
|
|
|
Таким же образом рассматриваются еще два случая, когда вторая производная отрицательна, т.е. f ″(x) < 0 на отрезке [a, b].
Следующая теорема обобщает все четыре случая для приближенного решения нелинейного уравнения (2.1) по методу хорд.
Теорема 2.2. Пусть функция y = f(x) на отрезке [a, b] удовлетворяет условиям теорем 2.1, т.е. уравнение (2.1) имеет на этом отрезке единственный корень.
Если функция y = f(x) имеет вторую производную, сохраняющую знак на этом отрезке, то исходя из начального приближения х0, удовлетворяющего условию (2.11), можно
вычислить корень уравнения (2.1) с заданной точностью по формулам (2.13) или (2.14).
2.2.3. Метод Ньютона (метод касательных)
Пусть уравнение (2.1) f(x) = 0 на отрезке [a, b] имеет единственный корень, причем производные f′(x) и f′′(x) непрерывны и сохраняют определенные знаки на этом отрезке.
Геометрический метод Ньютона эквивалентен замене небольшого участка дуги кривой y = f(x) касательной, проведенной в некоторой точке этой кривой (рис. 2.8).
38
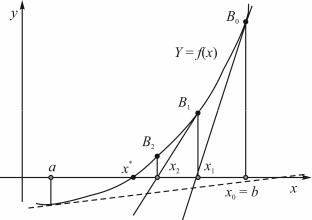
Рис. 2.8. Схема метода касательных
Положим для определенности f ′′(x) > 0 для x [a, b]
иf(b) > 0.
1.Для построения итерационной последовательности по методу касательных выберем начальное приближение (нулевую итерацию) x0 = b. исходя из условия
f(x0) f ′′(x0) > 0. |
(2.15) |
2. Проведем касательную к кривой y = f(x) в точке
B0[x0, f (x0)].
3.В качестве первого приближения корня х1 возьмем абсциссу точки пересечения этой касательной с осью ОХ.
4.Через точку B1[x1, f(x1)] снова проведем касательную, абсцисса точки пересечения которой с осью ОХ даст
нам второе приближение корня х2.
Аналогичным образом строим итерационную последовательность
х0 = b, x1, x2,……., xn,….
В математическом анализе доказывается теорема, что эта итерационная последовательность сходится к точному решению х* уравнения (2.1).
39

Для получения (n + 1)-й итерации хn+1 запишем нение касательной к нашей кривой в точке Bn[xn, (n = 0, 1, 2, ….)
y – f(xn) = f ′(xn) (x – xn).
урав- f(xn)]
Полагая y = 0, x = xn+1, получим формулу для построения последовательности приближений корня уравнения (2.1):
x |
x |
|
f (xn ) |
. |
(2.16) |
|
|||||
n 1 |
n |
|
f '(xn ) |
|
|
|
|
|
|
||
Если в нашем случае положить x0 = а, т.е. условие (2.15) не выполняется, то, проведя касательную к кривой y = f(x) в точке (a, f(a)), мы получили бы точку х (см. рис. 2.8), лежащую вне отрезка [a, b]. Выбранное таким образом начальное приближение оказывается непрактичным. В данном случае «хорошим» начальным приближением х0 является то, для которого выполняется условие (2.15).
В математическом анализе доказывается теорема, обобщающая это правило.
Теорема 2.3. Пусть функция y = f(x) на отрезке [a, b] удовлетворяет условиям теорем 2.1, т.е. уравнение (2.1) имеет на этом отрезке единственный корень.
Если функция y = f(x) имеет вторую производную, сохраняющуюзнак наэтомотрезке, то исходяизначального приближениях0, удовлетворяющего условию (2.15), можно вычислить корень урав-
нения (2.1) сзаданнойточностью поформуле (2.16).
Метод касательных хорошо реализуется на ЭВМ.
Замечания
1. Из формулы (2.16) видно, что чем больше значения f ′(x) в окрестности корня х*, тем меньше поправка, которую нужно прибавить к n-му приближению, чтобы получить (n + 1)-е приближение. Поэтому метод касательных особенно удобно применять тогда, когда график функции y = f(x) имеет большую кривизну в окрестности корня соответствующего уравнения, т.е. круто меняет свое значение.
40
