
книги / Численные методы решения задач строительства. Ч. 1
.pdf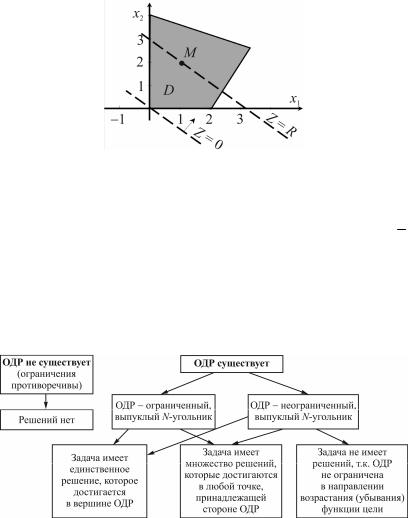
Рис. 6.8. Графический метод поиска экстремума функции
Стоящую перед нами задачу (6.8)–(6.9) можно сформу-
лировать следующим образом: среди всех точек (x1, x2) D найти такую, координаты которой минимизируют функцию цели (6.8).
В зависимости от области допустимых решений (ОДР) возможны следующие варианты решения задачи линейного программирования (рис. 6.9).
Рис. 6.9. Варианты решения задач ЛП
2. Приравняем выражение функции цели какой-либо постоянной величине R:
Zmin c1x1 c2 x2 |
R. |
(6.10) |
131
Это уравнение определяет на плоскости прямую, в точках которой функция цели Z принимает постоянное значение
R.Такая прямаяназывается линиейуровняфункциицели.
3.Будем изменять величину R, т.е. перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. Направление движения прямой для нашего примера (с2 > 0) указано на рис.
6.10стрелкой.
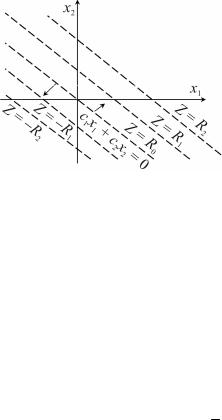
Рис. 6.10. Линии уровня целевой функции
4.Таким образом, можно сказать, что при возрастании
R от – до + линия уровня (6.10), смещаясь параллельно самой себе в одну и ту же сторону, «зачерчивает» всю плоскость.
5.В результате либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции
вобласти допустимых решений.
6.Определим координаты точки экстремума функции цели и вычислим ее значение в этой точке.
Очевидно, что в нашем случае это будет первая точка
встречи линии уровня функции с областью D (см. рис. 6.8) при ее смещении от меньших значений R к большим, и эта
132

точка совпадает с началом координат. Для любой другой точ-
ки из области D значение функции цели Zmin будет больше, чем вточке(0,0).
Рассмотрим несколько типичных примеров геометрического решения задач линейного программирования.
Пример 6.2. Минимизировать целевую функцию
|
Zmin 1 x y |
(6.11) |
|
при ограничениях: |
|
|
|
P1 : |
x y 1 0, |
|
|
P2 : 3x 2y 6 0, |
|
||
P3 |
: |
3x y 9 0, |
(6.12) |
P4 |
: |
x 0, |
|
P5 |
: |
y 0. |
|
Строим полуплоскости Pi, i = 1, 2, 3, 4, 5, соответствующие каждому неравенству системы ограничений (6.12).
Полуплоскость Р1 ограничена прямой x – y + 1= 0 и распо-ложена «снизу» от этой прямой. Аналогично строим полуплоскости Р2 и Р3. Пересечение полуплоскостей Р1,
Р2, Р3 и x 0, y 0 дает многоугольник D (рис. 6.11). Записываем прямую линии уровня функции цели
1 x y R
и строим прямые, соответствующие R = –1, R = 0 и R = 1. Из рис. 6.12 видно, что линию уровня нужно перемещать в сторону уменьшения значения R до встречи с «последней» точкой области, т.е. М(2,3) в которой функция цели принимает значение Zmin = – 4.
Таким образом, решением задачи является x = 2, y = 3,
Zmin= – 4.
Решение данной задачи с использованием электронных таблиц Excel приведено в подразд. 6.5.
133

Рис. 6.11. Область допустимых решений D (к примеру 6.2)
Пример 6.3. Минимизировать целевую функцию
Zmin x y |
(6.13) |
при ограничениях примера 6.2.
Область допустимых решений уже построена в предыдущем примере. Строим линии уровня x y R для R = 0
и R = –1.
Рис. 6.12. Область допустимых решений D (к примеру 6.3)
134
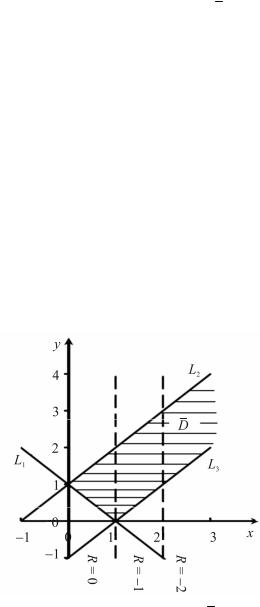
Из рис. 6.12 видно, что при перемещении линии уровня R соприкосновение с областью D произойдет по границе области.
Задача имеет бесконечно много решений. В ряде случаев можно выбрать одно из них исходя из физического смысла задачи.
Пример 6.4. Минимизировать функцию цели
Zmin x.
Система ограничений имеет вид
x y 1 0,x y 1 0,
x y 1 0,x 0, y 0.
(6.14)
(6.15)
Построим область допустимых решений, определяемую системой неравенств (6.15), аналогично примеру 6.2 (рис. 6.13).
Рис. 6.13. Области допустимых решений D (к примеру 6.4)
135
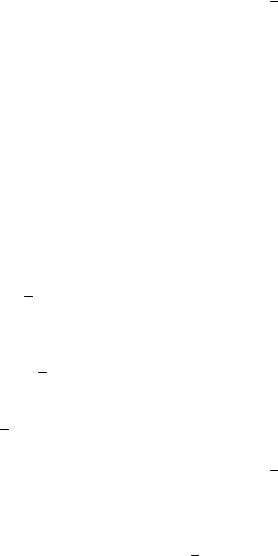
Строим линии уровня
–x = R для R = 0, R = –1, R = –2. Очевидно, что для
всех R (– , 0] линии уровня пересекают область D . Следовательно, функция цели не ограничена снизу, т.е.
Zmin .
Пример 6.5. Рассмотрим предыдущую задачу на поиск максимума функции цели, т.е. ограничения описываются системой (6.15), а функция цели имеет вид
Zmax x. |
(6.16) |
Из рис. 6.13 видно, что максимальное значение функция цели достигает в начале системы координат, т.е. решением задачи является x = 0, y = 1 и, соответственно, Zmax = 0.
Обобщим результаты приведенных выше решений задач линейного программирования (6.8)–(6.9). При решении этих задач возможны различные случаи.
1.При перемещении линии уровня соприкосновение
еес областью D произойдет по целому отрезку границы области. В этом случае решений бесконечно много. Именно такой случай рассмотрен в примере 6.3. В таких случаях надо обратиться к физической интерпретации задачи.
2. Область D является неограниченной фигурой, и прямая уровня Z R для сколь угодно больших по абсолютной величине отрицательных R имеет общие точки
с областью D . В этом случае минимальное значение функции цели в области равно – . Линия уровня –x = R при всех значениях R R 0 пересекает область D . Сле-
довательно, функция цели в области не ограничена снизу,
т.е. Zmin , иначе говоря, минимум функции не достига-
ется. Такой случай приведен в примере 6.4.
3. Область допустимых решений D пуста, и задача
(6.8)–(6.9) в этом случае не имеет решения.
136

4. Область допустимых решений D содержит единственную точку. В этом случае не приходится говорить об оптимальном решении.
В случае n неизвестных (n 3) все построения теряют наглядность. Однако геометрическая формулировка задачи в случае n неизвестных остается той же самой, что и в случае двух переменных. Различие состоит в том, что понятие «линия уровня» для n = 2 заменяется понятием «плоскость уровня» для n = 3 и «гиперплоскость» – для n > 3.
6.3.4. Симплекс-метод решения задач линейного программирования
Двумерные задачи линейного программирования решаются графически. Для случая n = 3 нужно уже рассмотреть трехмерное пространство, и целевая функция будет достигать своего оптимального значения в одной из вершин многогранника.
В общем виде, когда в задаче участвуют n-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3, весьма затруднительно
идаже невозможно.
Сдругой стороны, обычный метод классического математического анализа для решения задач на условный экстремум неприменим для решения задач ЛП. Линейная
форма (6.4), определенная в области (6.5) D , достигает своего экстремума на границе (в вершинах) этой области, т.е. в точках, в которых частные производные могут быть отличны от нуля.
А поскольку экстремум функции цели (6.4) достигается в вершинах многогранника, то, казалось бы, достаточно
137

вычислить значение функции цели во всех вершинах многогранника, а затем найти ту из них, в которой функция достигает своего минимума или максимума. Но такой путь решения задач ЛП, даже с относительно небольшим числом ограничений и неизвестных параметров, практически неосуществим, так как процесс отыскания вершин весьма трудоемкий, а число вершин может оказаться астрономически большим.
Поэтому надо найти способ перехода от данной вершины к «лучшей», а от нее – к еще «лучшей». Кроме того, сюда же надо добавить какие-то условия существования оптимального решения для данной задачи.
В этом и заключается суть метода последовательного улучшения плана для решения задачи ЛП, который называется симплекс-методом и наиболее широко применяется в настоящее время.
Опишем идею симплекс-метода. Пусть данная задача ЛП является задачей минимизации и имеет непустое мно-
жество допустимых решений |
(многогранная область |
|
|
D |
|||
с конечным числом вершин). |
Тогда каким-либо способом |
||
(они существуют) найдем какую-нибудь вершину области
D и все ребра, выходящие из этой вершины. Пойдем по одному из ребер, вдоль которого функция цели убывает.
Достигаем следующей вершины, находим выходящие из нее ребра и повторяем процесс. Когда мы доберемся до вершины такой, что вдоль всех выходящих из нее ребер функция возрастает, то эта вершина и дает оптимальное решение, т.е. в этой вершине и достигается минимум.
Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
138
Реализация симплекс-метода унифицирована, все вычисления проводятся с помощью специального вида таблиц (симплекс-таблиц). С другой стороны, метод хорошо программируется, и в настоящее время существуют всевозможные пакеты прикладных программ, включающие и реализацию симплекс-метода.
Широкое распространение электронных таблиц, таких, например, как Microsoft Excel, позволяет эффективно решать всевозможные задачи линейного программирования.
6.4.Примеры задач линейного программирования
всфере проектирования и управления строительным производством
Имеется много данных об успешном использовании моделей ЛП в различных задачах управления и проектирования в строительстве. Рассмотрим некоторые схемы таких задач.
6.4.1. Задача об оптимальном плане выпуска продукции
Основной формой деятельности любого предприятия является производство тех или иных видов продукции. При этом в процессе производства предприятие потребляет (расходует) определенные виды ресурсов (труд, сырье,
оборудование, денежные средства, природные ресурсы
и т.п.). Поскольку обычно размеры ресурсов ограничены, возникают проблемы их рационального распределения.
Если предприятие выпускает продукцию нескольких видов с использованием одних и тех же ресурсов, то администрация должна решить, какое количество продукции каждого вида следует производить. Принятое решение будет направлено на удовлетворение определенной цели администрации (например, получить максимальную прибыль или минимизироватьзатраты производства).
139

Постановка задачи. Предприятие выпускает n видов продукции, на которую употребляет m видов сырья. Расход i-го вида сырья на единицу j-го вида продукции составляет aij единиц. Известно, что на каждой единице продукции j-го вида предприятие получает прибыль cj.
Требуется определить, сколько единиц каждого вида про-
дукции должно изготовить предприятие (оптимальный план выпуска продукции), чтобы обеспечить максимальную прибыль. При этом следует учесть, что запасов сырья каждого ( i-го) вида имеется bi .
В качестве проектных (управляемых) параметров в данной задаче можно принять объемы выпуска соответ-
ствующего вида продукции: X x1, x2 , ..., xn . Иначе говоря,
xi, i = 1, 2, …, n – количество единиц каждого i-го вида продукции, которое должно изготовить предприятие.
Математической моделью этой задачи служит следующая задача линейного программирования: найти максимум целевой функции (линейной формы):
n |
|
Zmax c1x1 c2 x2 cn xn ci xi |
(6.17) |
i 1
при выполнении ограничений
a11x1 a12 x2 a1n xn b1, |
|
|||||||
a x a x a x b |
, |
|
||||||
|
|
21 1 |
22 2 |
2n n |
2 |
|
|
|
|
|
|
|
(6.18) |
||||
|
|
|
||||||
a |
|
x a |
x a |
x b |
|
, |
||
|
m1 1 |
m2 2 |
|
mn n |
m |
|
||
x |
j |
0, |
j 1, 2, , n. |
|
|
|
||
|
|
|
|
|
|
|
|
|
Решение такой задачи позволит руководителю определить оптимальные объемы выпуска, выявить те виды продукции, выпускать которые в данных условиях нецелесообразно, а возможно, и сделать вывод об изменении номенклатуры.
140
