
книги / Численные методы решения задач строительства. Ч. 1
.pdf
ский ученый Дж. Данциг описал один из основных методов решения задач линейного программирования, получивший название «симплексный».
Выбор метода решения задачи оптимизации зависит от свойств целевой функции и той информации о ней, которая может считаться доступной в процессе решения задачи.
В зависимости от вида целевой функции и структуры ограничений в математическом программировании выделяют следующие основные разделы (рис. 6.3).
Если целевая функция (6.1) и система ограничений (6.2)–(6.3) линейны относительно проектных параметров, то задача математического программирования называется задачей линейного программирования (ЛП). Если нелинейны – нелинейного программирования. Если ставится до-
полнительное условие, чтобы переменные были целочис-
ленны – задача целочисленного программирования и т.п.
Рис. 6.3. Классификация задач математического программирования
Методы решения задач математического программирования имеют свою специфику в отличие от методов классического анализа отыскания экстремумов функций, так как даже в наиболее простых задачах (линейное программирование) экстремум достигается в угловых точках границы области допустимых решений, т.е. там, где нарушается дифференцируемость функций.
121

При этом в практических задачах число переменных и ограничений обычно столь велико, что если просто перебирать все точки, «подозреваемые» на экстремум, то вряд ли даже ЭВМ справится с такой задачей.
6.2. Постановка задачи оптимального проектирования
Под проектированием мы будем понимать процессы создания не только архитектурно-строительных объектов или конструкций, но и процессов управления предприятием (фирмой) в сфере организационно-хозяйственной или экономической деятельности, процессы создания новых композиционных материалов и т.п.
Постановка задачи оптимального проектирования ведется с учетом назначения реальных целей проектирования и конкретных условий реализации проекта.
Процесс проектирования имеет целью получение оптимального объекта, имеющего возможно наилучшие свойства. Например, такие как минимальный вес, минимальная стоимость, максимальные прочностные характеристики, максимальная энерговооруженность, максимальная прибыль, минимум капиталовложений и т.п.
Постановка задачи оптимального проектирования носит неформальный характер и включает следующие этапы:
определение входных (управляемых) параметров;
определение выходных параметров (переменных, определяющих состояния изучаемого объекта);
выбор целевой функции;
назначение ограничений.
Входными (управляемыми) параметрами задачи назы-
ваются величины х1, х2, …, хn, которые полностью характеризуют изучаемый процесс. Их обычно записывают в виде
вектора X (x1, x2 ,.., xn ) .
122

Качество функционирования любой системы характери-
зуется множеством выходных параметров Y y1, y2 ,.., ym ,
или критериевэффективности [8].
Переменныe y1, y2 ,.., ym – это параметры оптимизации
(или функции отклика, или целевые функции). Это зависи-
мые переменныe.
Параметр оптимизации – это реакция (отклик) на воздействие входных параметров, которые определяют поведение изучаемого объекта.
Чаще всего требуется установить зависимость между проектными параметрами и одним из выходных параметров, наиболее важным.
Параметр оптимизации может быть измерен количественно, а может представлять собой качественную сторону объекта. Поэтому все выходные параметры обычно делятся соответственно на количественные и качественные.
Качественные критерии могут принимать только два значения: 1 или 0. Это может быть, например, разрушение или неразрушение сооружения, прием или неприем на работу какого-то сотрудника и т.д. В таких случаях обычно используют вероятностный подход. В дальнейшем будем рассматривать только количественные параметры.
Целевая функция (6.1) количественно выражает качество объекта, и потому ее иногда называют также функцией качества или критерием оптимальности. Общая задача математического программирования состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
Назначение ограничений. Ограничения объективно появляются при проектировании технических объектов и объектов управления и вытекают из конкретной физической и технологической сущности задачи, например ограниченности ресурсов и т.п.
123
Ограничения представляют собой математическое описание требований, обеспечивающих функционирование проектируемого объекта. Ограничения подразделяются:
на экономические, включающие в себя ограничения ресурсов, требования к сбыту, торговле, организационной системе;
прочностные, обеспечивающие работоспособность конструкции в целом, отдельных ее узлов из условий прочности, жесткости, устойчивости, долговечности; условия равновесия, совместности деформаций, формула Мора для определения прогиба и т.п.;
конструктивно-технологические, описывающие спе-
циальные конструктивные или технологические требования;
механические, описывающие кинематические и динамические характеристики объекта (взаимное расположение узлов и элементов конструкции, внешние усилия, инерционные силы, массу конструкции и т.п.).
Ограничения могут иметь вид: равенств (6.2) и (или)
неравенств (6.3).
6.3. Задачи линейного программирования
Линейное программирование – направление матема-
тики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.
Термин линейное программирование – это, конечно, не составление программ для ЭВМ. Программирование здесь должно интерпретироваться как планирование, формирование планов, разработка программы действий.
Круг задач, решаемых при помощи методов линейного программирования, достаточно широк. Это, например:
задача об оптимальном использовании ресурсов при производственном планировании;
задача о смесях (планирование состава продукции);
124

задача о нахождении оптимальной комбинации различных видов выпускаемой продукции;
транспортные задачи (перемещение грузов);
анализ размещения социальных и производственных объектов (предприятий).
Рассмотрим общую постановку задач ЛП, некоторые схемы типичного применения и методы их решения.
6.3.1.Общая постановка задачи
Задача линейного программирования (ЛП) форму-
лируется в общем виде следующим образом [7]: требуется найти экстремум (min/max) линейной функции n независимых переменных (проектных параметров) x1, x2, ..., xn:
n |
|
Zmin c1x1 c2 x2 cn xn ci xi |
(6.4) |
i 1
при ограничениях, наложенных на переменные в виде линейных неравенств (или равенств) m > n:
a11x1 a12 x2 a1n xn b1, |
|||||||
a |
|
x a x a x b , |
|||||
|
21 1 |
22 |
2 |
2n n |
2 |
||
.......................................... |
(6.5) |
||||||
|
|
|
|
|
|
|
|
a |
|
x a |
x a x b , |
||||
|
m1 |
1 |
m2 |
2 |
mn n |
m |
|
x |
|
|
0, |
i 1, 2, , n. |
|
||
i |
|
|
|
|
|
|
|
Линейную функцию (6.4) – функцию цели принято называть линейной формой задачи ЛП.
Напомним, что множество параметров X (x1, x2 ,.., xn ), удовлетворяющих системе ограничений (6.5), называется
областью допустимых решений задачи (ОДР D ).
Допустимое решение X * x* , x* ,.., x* , дающее экстре- |
|
1 2 |
n |
мумфункции цели (6.4), называется оптимальным решением.
125
Наряду с задачей ЛП (6.4)–(6.5), называемой стандартной, существуют и другие задачи ЛП, имеющие различные формы записи. Например, система неравенств (6.5) может быть смешанной, т.е. наряду с неравенствами система ограничений может содержать и равенства, или проектные параметры могут быть не все неотрицательны. И, наконец, в ряде случаев требуется найти максимум линейной формы Zmax. Любая из них может быть сведена путем несложных математических преобразований к эквивалентной ей задаче любого другого вида.
6.3.2. Геометрический смысл системы линейных неравенств
Рассмотрим геометрическое истолкование задачи линейного программирования, а также геометрическую сущность симплекс-метода. Знакомство с геометрической интерпретацией задачи помогает наглядно представить смысл задачи, понять характер возможных осложнений.
Случай двух проектных параметров
Начнем с рассмотрения одного линейного неравенства с двумя параметрами х1, х2:
ax1 bx2 c 0. |
(6.6) |
Областью решения неравенства (6.6) является множество точек, удовлетворяющих этому неравенству, т.е. полу-
плоскость Р, ограниченная прямой L: ax1 bx2 c 0.
Прямая L разбивает всю плоскость на две полуплоскости. Для того чтобы определить, какую из двух полуплоскостей описывает неравенство (6.6), достаточно выбрать
точку M 0 x10 , x20 из одной из полуплоскостей. И если ко-
ординаты этой точки удовлетворяют неравенству, то оно и описывает именно эту полуплоскость. Саму прямую L считаем принадлежащей этой полуплоскости.
126
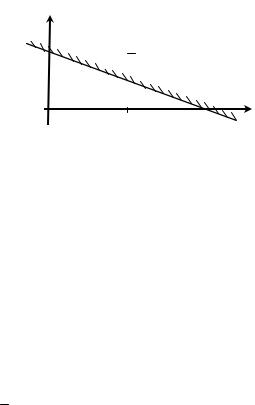
Пример 6.1. Найти полуплоскость, определяемую неравенством
x1 2x2 2 0.
Рассмотрим прямую x1 2x2 2 0, разбивающую всю
плоскость на две полуплоскости. Выбрав точку М(0,0), легко убедимся, что координаты ее не удовлетворяют исходному неравенству. Это означает, что неравенство определяет полуплоскость, расположенную «выше» этой прямой и саму эту прямую(рис. 6.4).
y
1 |
D |
x1
1 2
Рис. 6.4. Область решения неравенства
Случай m (m > 1) неравенств
Предположим теперь, что задано не одно неравенство, а система из m неравенств:
a |
|
x |
a |
x |
b 0, |
|
||
11 |
1 |
12 |
|
2 |
|
1 |
|
|
a21x1 |
a22 x2 |
b2 0, |
(6.7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
a |
|
x |
a |
|
x |
b 0. |
|
|
|
m1 1 |
m2 |
|
2 |
m |
|
||
Каждое неравенство определяет некоторую полуплос-
кость Pi, (i = 1, 2, ..., m). Областью допустимых решений системы неравенств (6.7) является некоторая многоугольная
область D , полученная в результате пересечения конечного числа полуплоскостей, описываемых каждым отдельным не-
127
равенством. Если эта область ограничена, то ее называют
многоугольником допустимыхрешений системы(6.7).
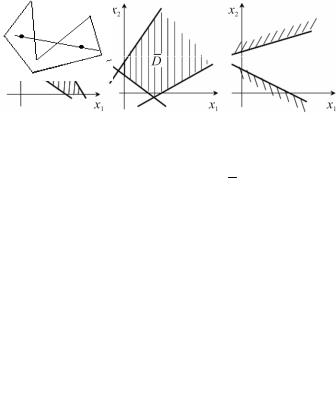
Область решения системы (6.7) может быть замкнутой ограниченной (рис. 6.5, а) или замкнутой неограниченной многоугольной областью (рис. 6.5, б), а может быть и пустой
(рис. 6.5, в), когда система (6.7) противоречива.
a |
б |
в |
Рис. 6.5. Области допустимых решений системы неравенств
Область допустимых решений D обладает важным свойством – она является выпуклой.
Область называется выпуклой, если она расположена по одну сторону прямой, проходящей через какой-либо отрезок границы области. Или когда две произвольные точки области можно соединить отрезком, полностью принадлежащим этой области (рис. 6.6).
а |
б |
Рис. 6.6. Области: выпуклый многоугольник (а); невыпуклый многоугольник (б)
Выпуклость многоугольника решений вытекает из способа его построения: он получен путем пересечения нескольких полуплоскостей.
128
Случай n проектных параметров
Сказанное выше можно обобщить для случая n проектных параметров. Система ограничений в этом случае имеет вид (6.5).
Каждое неравенство системы ограничений (6.5)
Pi : ai1x1 ai2 x2 ain xn bi |
(i 1,2, ,m) |
определяет некоторое полупространство Pi, а все неравенства – некоторую область в n-мерном пространстве, которая является пересечением конечного числа полупространств.
По аналогии с двумерным случаем называем эту область в n-мерном пространстве выпуклой многогранной областью, а в случае ее ограниченности – выпуклым много-
гранником.
Совокупность точек n-мерного пространства, координаты которого удовлетворяют системе (6.5), есть замкнутая
выпуклая многогранная область D , получающаяся в резуль-
тате пересечения всех m полупространств, отвечающих неравенствам системы. Если эта область ограничена, мы называ-
ем ее выпуклым многогранником впространстве.
Опорной прямой (при n = 2) |
L1 |
|
называется прямая, которая име- |
||
|
ет с областью D по крайней мере одну общую точку. При этом
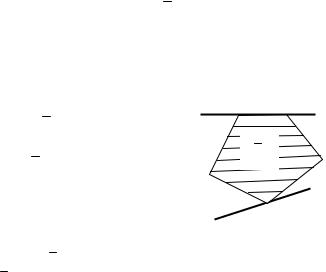
вся область D расположена по одну сторону от этой прямой. Например, на рис. 6.7 приведены две опорные прямые: L1 и L2. Прямая L1 проходит через вершину области D , а L2 – через сторону D .
D
L2
Рис. 6.7. К определению опорной прямой
129

При n = 3 уже говорят об опорной плоскости, которая может проходить через вершину многогранника, или его ребро, или его грань. Понятие опорной плоскости (гиперплоскости) легко обобщить на случай n > 3.
6.3.3. Геометрический метод решения задач линейного программирования
Рассмотрим геометрическое истолкование задачи линейного программирования для случая двух проектных параметров. При рассмотрении геометрического смысла задачи ограничения удобно задавать в виде неравенств, как мы и сделаем в этом разделе.
Постановка задачи. Пусть задана целевая функция для двух проектных параметров x1 и x2:
Zmin c1x1 c2 x2 . |
(6.8) |
Для определенности положим c2 0 . И пусть задана система линейных неравенств
a11x1 a12 x2 b1 0, |
|
|||||||
a |
x a |
x |
b |
0, |
|
|||
|
|
|
21 1 |
22 |
2 |
2 |
|
|
|
.. |
(6.9) |
||||||
|
||||||||
a |
|
x a |
x |
b |
0. |
|
||
|
|
m1 1 |
m2 2 |
m |
|
|
||
x |
|
0, |
x |
|
0. |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
Требуется среди допустимых решений системы неравенств (ОДР) найти такое, при котором целевая функция принимает минимальное значение.
Последовательность действий:
1.Строим область допустимых решений системы (6.9).
Вобщем виде – это выпуклая замкнутая многоугольная об-
ласть D на плоскости x1x2, лежащаявпервойчетверти. Предположим, что эта область имеет вид, как показано
на рис. 6.8.
130
