Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Числовые и степенные ряды. Ряды Фурье

.pdf

Скачиваний:

Добавлен:

20.11.2023

Размер:

972.67 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

= π12 (−1 + (−1)n + (−1)n − 1) = π22 ((−1)n − 1). n n

an = π2n2 ((−1)n − 1) = π−n22 (1 − (−1)n ).

					bn = 1	π
					bn = 1	f ( x) sin (nx)dx =
					π	− π
	1		0	(− x − 1) sin		(nx)dx +	1	π
=	1			(− x − 1) sin		(nx)dx +	1	(x + 1) sin (nx)dx =
	π	− π					π	0
			1	0	(x + 1) sin (nx)dx + 1				π
= −			1		(x + 1) sin (nx)dx + 1				(x + 1) sin (nx)dx.
			π − π				π		0

Вычислим неопределённый интеграл по частям:

(x + 1) sin (nx)dx =

u = x + 1,

dv = sin (nx)dx

du = dx,

v = −

cos(nx)

= ( x + 1) −

cos(nx)

− −1 cos(nx)dx =

= (x + 1) −

cos(nx)

cos(nx)dx =

= (x + 1) −

cos(nx)

1 sin (nx) + C =

= −n1( x + 1)cos(nx) + n12 sin (nx) + C.

Вычислили неопределённый интеграл:

(x + 1) sin (nx)dx = −n1(x + 1)cos (nx) + n12 sin (nx) + C.

Тогда

(x + 1) sin (nx)dx + 1

bn = −

( x + 1) sin (nx)dx =

π − π

−1

( x + 1)cos(nx) +

sin (nx)

−π

−1

(x + 1)cos(nx) +

sin (nx)

−1

cos(0) +

sin (0) −

(−π + 1)cos(−nπ)

sin (−nπ)

1 −1

(π +

1)cos(nπ) +

sin (nπ) −

−1

cos 0

sin 0

−1 −1

cos(0)

(−π + 1)cos(nπ)

−1

(π + 1)cos(nπ) +

cos0 =

= n1π (cos(0) − (−π + 1)cos(nπ) − (π + 1)cos(nπ) + cos (0)) =

=n1π (2cos (0) − ((−π + 1) + (π + 1))cos (nπ)) =

=n1π (2 − 2cos(nπ)) = n2π (1 − (−1)n ).

bn = π2n (1 − (−1)n ).

Нашли коэффициенты Фурье:

a0 = 2, an = π−n22 (1− (−1)n ), bn = π2n (1− (−1)n ).

Разложение функции f (x) в ряд Фурье имеет вид

∞	−2			n		2			n
f ( x) = 1 +			(1 − (−1)		) cos(nx) +		(1	− (−1)		) sin (nx) .
f ( x) = 1 +	πn	2	(1 − (−1)		) cos(nx) +	πn	(1	− (−1)		) sin (nx) .
n=1	πn					πn

Найдём разложение функции в ряд в развёрнутом виде. Выпишем коэффициенты ряда

a0 = 2, an = π−n22 (1− (−1)n ), bn = π2n (1− (−1)n ).

−2

−4

−2

a1 =

+ 1) =

;

a2 = 4π (1

− 1) = 0;

−2

−4

−2

a3 =

9π

(1 +

1) =

9π ;

a4 =

(1 − 1) = 0;

16π

a2n−1 =

−4

; a2n = 0.

π (2n − 1)2

b1 =

(1 + 1) =

; b2 =

(1 − 1) = 0;

2π

b3 =

+ 1) =

;

b4 =

− 1) = 0;

3π

4π

b2n−1

;

b2n = 0.

π (2n − 1)

Все чётные коэффициенты (2n)

в разложении равны нулю.

Нечётные

коэффициенты

(2n −1)

отличны от нуля. Разложение

функции

f (x) можно записать так:

∞

−1

f ( x) = 1 +

cos((2n − 1) x) +

sin ((

2n − 1) x) =

(2n − 1)

π n=1 (2n − 1)

= 1+

−cosx + sinx −

cos3x +

sin3x −

cos5x +

sin5x − … .

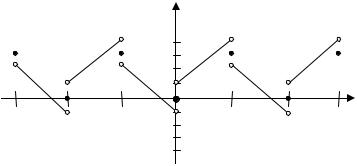
Найдем сумму S (x) ряда Фурье. Функция f (x) имеет x = 0

точку разрыва 1-го рода. Сумма ряда S ( x)						в точке x = 0
S (0) =	f (−0) + f (+0)		= −1 + 1 = 0.

2			2
На концах отрезка, в точках x = − π и x = π , сумма S (x) ряда
		S (−π)	= S (π) =	f (−π + 0) + f (π − 0)			=
				2

	=	(− (−π) − 1) + (π + 1)			= π − 1+ π + 1 = 2π		= π.

			2	2		2
На интервалах			непрерывности сумма S (x)				ряда совпадает
с функцией f (x) . Сумму S (x)				ряда Фурье можно записать так:

− x − 1, − π < x < 0,x + 1, 0 < x < π,

S ( x) = 0, x = 0,

π, x = −π, x = π.

График суммы ряда Фурье изображен на рис. 2.

						y = S(x)
			1
–3π	–2π	–π	0			x
–3π	–2π	–π	–1	π	2π	3π

Рис. 2

3.4. Разложение в ряд Фурье чётных и нечётных функций

Определение 9. Пусть функция y = f (x) определена на мно-

жестве D и для любого	x D выполнено условие −x D (т.е. об-
ласть D симметрична относительно начала координат). Функция
y = f (x) называется	чётной, если выполняется условие

f (−x) = f (x); нечётной, если f (−x) = − f (x) .

График чётной функции симметричен относительно оси OY, график нечётной функции симметричен относительно начала координат.

Если функция f (x) – чётная на отрезке [−a;a] , то

	а	а
	f ( x)dx = 2 f ( x)dx.
	− а	0
Если функция	f (x)	– нечётная на отрезке [−a;a] , то
		a
		f ( x)dx = 0.
		− a
Рассмотрим разложение чётных и нечётных функций в ряд
Фурье.	f (x)
Если функция	f (x)	чётная на отрезке [–π;π] , то произведе-
ние f (x) cos(nx)	– чётная функция, f (x) sin(nx) – нечётная

функция. Вычисляем коэффициенты ряда Фурье:

an = π1

− π

		1	π	2	π
a0	=		f (x)dx =		f (x)dx.
		π		π
			− π		0

f( x) cos(nx)dx = 2 π f ( x) cos(nx)dx.

π0

	1	π
bn =	1	f (x) sin (nx)dx = 0.
	π	− π

Получили неполный ряд Фурье, содержащий косинусы:

				a0		∞
		f ( x) =		a0		+ an cos(nx).			(42)
		f ( x) =				+ an cos(nx).			(42)
			2			n=1
Если функция		f (x)	нечётная на отрезке [–π;π] , то произве-
дение f (x) cos(nx)		– нечётная функция, f (x) sin(nx)							– чётная
функция. Вычислим коэффициенты ряда Фурье:
			= 1		π
		a0	= 1		f (x)dx = 0.
			π − π
	an = 1		π
	an = 1		f ( x) cos(nx)dx = 0.
		π	− π
bn = 1	π						2	π
	f (x) sin (nx)dx =						2	f ( x) sin (nx)dx.
	f (x) sin (nx)dx =						π	f ( x) sin (nx)dx.
π	− π						π	0

Получили неполный ряд Фурье, содержащий синусы:

∞
f (x) = bn sin (nx).	(43)

n=1

Пример 42. Разложить в ряд Фурье функцию f (x) = x2 периода 2π , заданную на отрезке [–π;π] . График функции изображен

на рис. 3.

С помощью полученного разложения найти сумму числового

ряда:

S = 12 = 1+ 12 + 12 + 12 + … + 12 + …

∞

n=1

Функция f (x) = x2

– чётная,

следовательно, b = 0 . Найдём

коэффициенты a0 и an :

a =

π x2 dx =

π = 2π3

= 2π2 .

0 3π

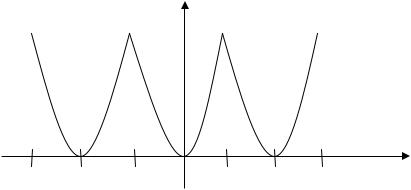
y = f(x)

–3π	–2π	0	π	2π	3π	x
		–π
			Рис. 3

u = x2

dv = cos(nx)dx

an =

0 x2 cos(nx)dx =

du = 2xdx

v =

sin (nx)

π sin (nx)

−

2xdx =

u = x,

dv = sin (nx)dx,

= −

0 x sin (nx)dx =

du = dx,

−cos(nx)

πn

v =

= −

−cos(nx)

π −

−cos(nx)

dx =

πn

π −

x cos(nx)

cos(nx)dx =

πn

π cos(nπ) −

sin (nx)

= (−1)n

πn2

πn3

Коэффициенты разложения

a	=	2π2	,	a = (−1)n	4	.
0		3		n	n2

Получили неполный ряд Фурье, или косинус-разложение:

f ( x) =

π2

+ 4

−cosx +

cos2x

−

cos3x

cos4x

−

cos5x

+ …

π2

∞

(−1)n

+ 4

cos(nx).

n=1

Сумма

S (x) ряда совпадает

функцией

f (x) :

S (x) = f (x) = x2 на отрезке [–π;π] .

С помощью полученного разложения найдём сумму числового

ряда:

S = 12 = 1+ 12 + 12 + 12 + … + 12 + … .

∞

n=1

Подставим в разложение x = π , получим

f (π) =

π2

+ 4

cos2π

−

cos3π

cos4π

−

cos5π

−cosπ +

+ …

π2

+ 4 1+

+ … +

+ …

= π2

+ 4S.

f (π) = π2 + 4S. 3

По условию f (π) = π2 , тогда

π2 = π2 + 4S, 3

4S = π2 − π2 = 2π2 , 3 3

S = π2 . 6

С помощью разложения функции в ряд Фурье нашли сумму числового ряда:

∞	1		1		1		1		1		2
		= 1+		+		+		+ … +		+ … =	π .
	2		2		2		2		2
n=1	n		2		3		4		n		6

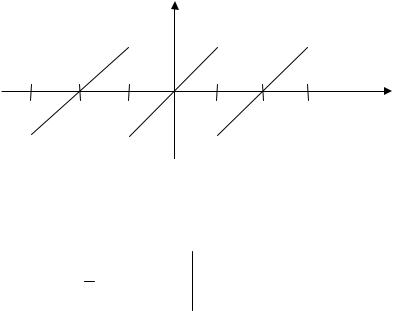
Пример 43. Разложить в ряд Фурье функцию f (x) = x периода 2π , заданную на отрезке [–π;π] . График функции изображен на рис. 4.

				π		y = f(x)
							x
			0		2π	3π
–3π	–2π	–π	0	π
–3π	–2π	–π		π
				–π
				Рис. 4
Функция		f (x) = x	– нечётная,		следовательно, a0 = an = 0 .

Найдём коэффициент bn :

bn = 2 π x sin (nx)dx = π 0

=	2	x	−cos(nx)
			n
	π

= −πn2 x cos(nx)

u = x,

dv = sin (nx)dx,

du = dx,

v =

−cos(nx)

π −

π +

cos(nx)dx =

πn

−2

π cos(nπ) +

sin (nx)

π =

−2 (−1)n = (−1)n+1

2 .

πn

πn2

f (x) = 2 sinx − sin2x

+ sin3x − sin4x

+ sin5x

− …

= 2 (−1)

n+1

sin (nx).

∞

n=1

Получили неполный ряд Фурье по синусам, или синусразложение. В точках непрерывности функции на интервале (−π;π)

сумма S (x) ряда Фурье совпадает с функцией S (x) = f (x) = x .

На концах отрезка,

в точках x = − π и x = π , сумма S (x) ряда

Фурье

S (−π) = S (π) =

f (−π + 0) + f (π − 0)

−π + π

= 0.

Сумма ряда Фурье

− π < x < π,

S ( x) =

x = −π, x = π.

Сумма ряда Фурье изображена на рис. 5.

y = S(x)

–3π

–2π

–π

2π

3π

–π

Рис. 5

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в папке книги

#
20.11.20238.37 Mб0Численные методы. Ч. 2.pdf
#
20.11.20237.06 Mб1Численные методы. Ч. 3.pdf
#
20.11.20236.88 Mб1Численные методы. Ч. 4.pdf
#
20.11.20237.5 Mб2Численные методы. Ч. 5.pdf
#
20.11.2023755.42 Кб0Численный расчёт стержневых систем..pdf
#
20.11.2023972.67 Кб2Числовые и степенные ряды. Ряды Фурье.pdf
#
20.11.20233.44 Mб1Чтение и перевод юридических текстов..pdf
#
20.11.2023605.64 Кб3Что нужно знать о зарубежных партнёрах особенности культуры, деловой этикет, переговоры..pdf
#
20.11.20238.48 Mб0Что такое философия..pdf
#
20.11.202346.99 Mб1Чугуны. Структура и термическая обработка.pdf
#
20.11.2023740.01 Кб4Шасси автомобиля. Элементы расчета и эксплуатационная надежность.pdf