
книги / Числовые и степенные ряды. Ряды Фурье
.pdf
Пример 30. Разложить функцию f (x) = lnx в ряд Тейлора в окрестности точки x0 = 1.
Воспользуемся рядом Тейлора:
f (x) = f ( x0 ) + |
f ′ (x0 ) |
( x − x0 ) + |
f ′′ (x0 ) |
( x − x0 ) |
2 |
+ … |
1! |
2! |
|
||||
|
|
|
|
|
… + f (n)n(!x0 ) ( x − x0 )n + …
Найдём коэффициенты разложения:
f (1) = ln1 = |
0, |
f ′ (x) = (lnx)′ = |
1 |
, f ′ (1) = 1. |
|
|
|
x |
|
f ′′ (x) = 1 |
′ |
= (x−1 )′ = −1 x−2 , f ′′(1) = −1. |
||
x |
|
|
|
|
f ′′′(x) = (−1)(x−2 )′ = −1(−2) x−3 , f ′′′(1) = −1(−2).
f (4) ( x) = (−1)(−2)(x−3 )′ = −1(−2)(−3) x−4 , f (4) (1) = −1(−2)(−3).
Наблюдается |
закономерность: |
f ′′(1) = −1, |
f ′′′(1) = 2!, |
f (4) (1) = −3!, тогда |
f (n) (1) = (−1)n+1 (n − 1)!. |
|
|
Подставим найденные значения в ряд Тейлора:
lnx = 1!1 ( x − 1) − 2!1 (x − 1)2 + 2!3!( x − 1)3 − 3!4!( x − 1)4 + …
… + (−1)n+1 (n − 1)!(x − 1)n + … . n!
Упростив коэффициенты, получим разложение функции в ряд Тейлора:
lnx = ( x − 1) − 12 ( x − 1)2 + 13 ( x − 1)3 − 14 ( x − 1)4 + …
… + (−1)n+1 (x − 1)n + … . n
41
Найдём интервал сходимости полученного ряда. Общий член ряда
un ( x) =
По признаку Даламбера
lim |
|
un+1 ( x) |
|
= lim |
|
(x − 1)n+1 |
|||||
|
|
|
|||||||||
|
un ( x) |
|
|
n + 1 |
|
||||||
n→∞ |
|
|
n→∞ |
|
|
||||||
|
|
= lim |
|
( x − 1) n |
|
|
= |
||||
|
|
|
|
||||||||
|
|
|
n→∞ |
|
|
n + 1 |
|
|
|
||
|
(−1)n+1 ( x − 1)n . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
: ( x − 1)n |
|
|
= lim |
|
( x − 1)n+1 |
|
n |
|
|
|
= |
||||||||||
|
|
|
|
|
|||||||||||||||||
|
( x − |
1) |
n |
||||||||||||||||||
|
n |
|
|
n→∞ |
|
|
|
n + 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x − 1 |
|
|
|
|
n |
|
|
|
|
|
|
x − 1 |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
= |
|
|
< |
1. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Раскроем модуль |
|
x −1 |
|
<1, |
−1< x −1< 1, |
|
интервал сходимости |
||||||||
|
|
|
|||||||||||||
0 < x < 2. |
|
|
|
|
|
|
|
|
|
|
|
||||
Проверим сходимость ряда на концах интервала. |
|
|
|||||||||||||
При x = 0 получим ряд (−1) |
n+1 |
(−1) |
n |
|
= (−1) |
2n+1 |
= −1. |
||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
∞ |
||
|
|
|
|
|
|
|
|
|
|
|
n=1 n |
n=1 n |
|||
|
|
|
|
n=1 |
|
|
n |
|
|
||||||
Гармонический ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∞ |
|
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
(−1) . |
|
|
|
|
|
|
|||||
При x = 2 получим ряд |
|
|
|
|
|
|
|||||||||
|
|
|
|
n=1 |
|
n |
|
|
|
|
|
|
|
|
|
Знакочередующийся числовой ряд сходится условно по при- |
|||||||||||||||
знаку Лейбница. |
|
|
|
|
|
|
|
|
|
|
|
||||
Интервал сходимости 0 < x ≤ 2. |
|
|
|
|
|
|
|
|
|
||||||
Замечание. При разложении функции в степенной ряд необ- |
|||||||||||||||
ходимо находить интервал сходимости. |
|
|
|
|
|
|
|
||||||||
Пример 31. Найти разложение |
|
в |
ряд |
|
|
Маклорена |
функции |
||||||||
f (x) = arctgx.
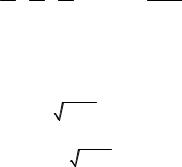
Находить разложение в степенной ряд данной функции по определению трудоёмко, так как надо вычислять производные и выявлять закономерность. Воспользуемся представлением данной функции в виде интеграла
42
|
|
x |
dt |
|
|
|
|
||
|
|
arctgx = 0 |
|
. |
|
|
|
|
|
|
|
1+ t2 |
|
|
|
|
|||
Подынтегральную функцию |
f ( x) = |
|
|
1 |
разложим в ряд |
||||
1 |
+ x2 |
||||||||
Маклорена, используя разложение |
|
|
|
||||||
|
|
|
|
|
|
||||
|
1 |
= 1 + x + x2 + x3 + x4 + x5 + … + xn + … |
|||||||
1 − x |
|||||||||
|
|
|
|
|
|
|
|||
с областью сходимости x (−1;1). Заменимв разложении хна (−t2 ):
f (t ) = |
|
|
1 |
= 1 − t2 + t4 − t6 + t8 − t10 + … + (−1)n t2n + … . |
|
1 |
− (−t2 ) |
||||
|
|
||||
Область сходимости полученного разложения t (−1;1). Почленно проинтегрируем полученный ряд в пределах от 0 до х,
где |
|
x |
|
<1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
arctgx = x |
dt |
|
|
= x (1− t2 + t4 − t6 + … + (−1)n t2n + …)dt = |
||||||||
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
0 1+ t |
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
= x − |
x3 |
+ |
x5 |
− |
x7 |
+ … + (−1)n |
x2n+1 |
|
+ … . |
|||
|
|
|
|
|
|
|
2n + 1 |
|||||||||
|
|
|
|
|
|
|
3 |
|
5 |
7 |
|
|
||||
Получили разложение функции в степенной ряд:
arctgx = x − x3 + x5 − x7 + … +
3 5 7
Интервал сходимости x (−1;1). Пример 32. Представить интеграл
x2n+1
(−1)n 2n + 1 + … .
в виде ряда по степеням х:
x |
dx |
|
|
. |
|
|
1 − x |
4 |
|||||
0 |
|
|
|
|||
Подынтегральная функция |
|
1 |
. |
|||
|
|
|||||
|
1 |
− x4 |
||||
43
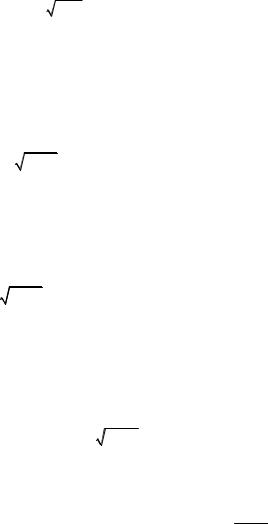
Воспользуемся частным случаем биноминального разложения функции в степенной ряд
1 |
|
= 1+ 1 x + |
1 3 |
x2 |
+ |
1 3 5 |
x3 + |
1 3 5 7 x4 |
|
1− x |
|
|
|
||||||
2 |
2 4 |
|
2 4 6 |
2 4 6 8 |
|||||
+ |
1 3 5 7 9 x5 + … = 1+ (2n − 1)!! xn |
||||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
n=1 (2n)!! |
||||
|
|
2 4 6 8 10 |
|
||||||
с областью сходимости x (−1;1). Заменим х на x4:
1 |
|
1 |
4 |
|
1 3 |
|
4 |
|
2 |
|
1 3 5 |
|
4 |
3 |
1 3 5 7 |
||
|
= |
1 + 2 x |
|
+ |
|
|
(x |
|
) |
|
+ |
|
(x |
|
) |
+ 2 4 6 8 |
|
1− x4 |
|
2 4 |
|
|
2 4 6 |
|
|||||||||||
|
+ |
|
1 3 5 7 9 (x4 )5 + … = 1 + (2n − 1)!! x4n . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 (2n)!! |
|||||||
|
|
|
2 4 6 8 10 |
|
|
|
|
|
|
|
|||||||
Тогда интеграл можно представить так:
+
(x4 )4 +
x
0
dx |
|
|
|
x |
|
|
|
1 |
|
4 |
|
1 |
3 8 |
1 3 5 12 |
|
(2n − 1)!! |
|
4n |
|
||||||||||||||||
|
|
|
= |
1 |
+ |
|
|
x |
|
+ |
|
|
|
|
|
x + |
|
|
|
|
|
x + … + |
|
|
|
|
|
x |
|
|
… dx = |
||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1− x |
|
|
|
|
|
|
2 |
|
|
|
2 |
4 |
|
2 4 6 |
|
|
|
(2n)!! |
|
|
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= x + |
1 x5 |
|
|
1 3 x9 |
|
1 3 5 x13 |
|
(2n − 1)!! |
|
x4n+1 |
|
||||||||||||||||||||||||
2 |
|
+ |
|
|
|
|
|
+ |
|
|
|
|
+ … + |
|
|
|
|
+ … . |
|||||||||||||||||
5 |
|
2 4 |
9 |
2 4 6 |
13 |
(2n)!! |
4n + 1 |
||||||||||||||||||||||||||||
Разложение интеграла можно записать так: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
dx |
|
|
= x 1+ |
|
∞ |
(2n − 1)!! xn dx = |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1− x |
|
|
|
|
|
(2n)!! |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
n=1 |
|
|
|
|
|
|
|
|
|
|
||||||||
= x1dx + x |
|
∞ |
(2n − 1)!! xn dx = x + |
||
|
|
|
(2n)!! |
|
|
0 |
0 |
n=1 |
|
||
|
|
|
|
= x + (2n − 1)!! |
|
|
|
|
|
∞ |
|
|
|
|
|
n=1 |
(2n)!! |
∞ x |
|
|
= |
|
|
|
(2n − 1)!! xndx |
||
|
(2n)!! |
|
|
|
n=1 |
0 |
|
|
|
x4n+1
4n + 1.
44

Интервалсходимости полученногорядасохраняется: x (−1;1).
Иногда приходится решать обратную задачу: по данному разложению найти сумму ряда или установить, к какой функции ряд сходится. Для этого используют почленное дифференцирование или интегрирование степенных рядов и стандартные разложения элементарных функций (см. приложение). В каждом случае необходимо определить, какой метод применить.
Пример 33. Применяя почленное дифференцирование или интегрирование, найти сумму степенного ряда:
x + |
x3 |
+ |
x5 |
+ |
x7 |
+ … + |
x2n−1 |
|
+ … . |
|
3 |
5 |
7 |
2n − 1 |
|||||||
|
|
|
|
|
||||||
Выберем метод, который будем применять. Общий член ряда
x2n−1
un (x) = 2n − 1.
Удобно применить метод почленного дифференцирования,
в этом случае сократится знаменатель |
(2n −1). Пусть сумма ряда |
|||||||||||
равна функции |
f (x), тогда |
|
|
|
|
|
|
|
|
|
||
|
|
x3 |
|
x5 |
|
x7 |
|
|
x2n−1 |
′ |
||
f ′ (x) = x + |
|
+ |
|
|
+ |
|
+ … + |
|
|
+ … = |
||
3 |
5 |
|
7 |
2n − 1 |
||||||||
|
|
|
|
|
|
|
|
|||||
|
= 1+ x2 + x4 + x6 + … + x2n−2 + x2n … . |
|||||||||||
Выберем |
порождающий |
|
ряд |
из |
приложения, похожий |
|||||||
на f ′(x), |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= 1 + x + x2 + x3 + x4 + x5 + … + xn |
|
1 − x |
||
|
с областью сходимости x (−1;1). Тогда
f ′(x) = 1+ x2 + (x2 )2 + (x2 )3 + … + (x2 )n−1 + (x2 )n
+ …
∞ n
… = (x2 ) .
n=0
45

f ′ ( x) = 1 −1x2 .
Находим
f ( x) = x |
1 |
|
dt = |
1 ln |
|
1+ x |
|
. |
|
|
|
||||||
|
2 |
|||||||
0 1− t |
|
|
2 |
|
1− x |
|
|
|
|
|
|
|
|||||
Сумма степенного ряда
x + |
x3 |
+ |
x5 |
+ |
x7 |
+ … + |
x2n−1 |
|
+ … = |
1 |
ln |
|
1+ x |
|
|
||||||||||||||
3 |
5 |
7 |
2n − 1 |
2 |
|
1 |
− x |
|||||||
|
|
|
|
|
|
|
||||||||
с областью сходимости x (−1;1).
Пример 34. Применяя почленное дифференцирование или интегрирование, найти сумму ряда:
1 2 + 2 3x + 3 4x2 +…+ n(n +1) xn−1 + … .
Выберем метод, который будем применять. Общий член ряда un (x) = n(n +1) xn−1.
В этом примере лучше применить метод почленного интегрирования. Пусть сумма ряда равна функции f (x), тогда
S1 ( x) = x f (t )dt = x (1 2 + 2 3t + 3 4t2 + … + n(n + 1)tn−1 + …)dt =
00
=2x + 3x2 + 4x3 + …+ (n +1) xn + ….
Повторно проинтегрируем:
S2 (x) = xS1 (t )dt = x (2t + 3t2 + 4t3 + … + (n + 1)tn + …)dt =
00
=x2 + x3 + x4 + … + xn + xn+1 + … .
Выберем порождающий ряд из приложения, похожий на S2 (x),
46

1 |
= 1 + x + x2 + x3 + x4 + x5 + … + xn + … |
|
1 − x |
||
|
с областью сходимости x (−1;1). Тогда
S2 ( x) = x2 + x3 + x4 + … + xn + xn+1 + … = |
|
|
1 |
− 1 − x. |
|||||||
1 |
− x |
||||||||||
|
|
|
|
|
|
|
|
||||
S2 |
( x) = |
|
|
1 |
− 1 |
− x. |
|
|
|
|
|
1 |
− x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
Чтобы найти функцию f (x), продифференцируем полученное выражение два раза:
|
|
|
|
|
1 |
|
|
′ |
|
|
1 |
|
|
|
|
S1 |
′ |
( x) = |
|
|
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
|
− 1 |
= |
|
|
2 − 1. |
|||||||
(x) = S2 |
1 |
− x |
(1− x) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
′ |
|
2 |
|
|
|
|
|
f ( x) = S′( x) = |
|
|
|
|
− 1 |
= |
|
|
|
. |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
(1− x) |
2 |
|
|
|
|
3 |
|
||
|
|
|
|
|
|
|
|
|
|
(1 − x) |
|
||||
Сумма ряда |
|
|
|
|
1 2 + 2 3x + 3 4x2 + … + n(n + 1) xn−1 + … = |
|
2 |
, |
|
(1 |
− x)3 |
|||
|
|
с областью сходимости x (−1;1).
Пример 35. Разложить данную дробь в ряд по степеням х:
(1 − 2x)3(1 + 4x).
Разложим данную дробь на простейшие дроби:
3 |
= |
|
A |
+ |
|
B |
= |
A(1 + 4x) + B (1 − 2x) |
. |
(1 − 2x)(1 + 4x) |
|
1 − 2x |
|
1 + 4x |
(1 − 2x)(1 + 4x) |
47

A(1+ 4x) + B(1− 2x) = 3.
|
|
|
|
|
|
|
|
x = |
1 |
, A(1 + 2) = 3 A = 1. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x = − |
1 |
|
|
|
|
1 |
|
|
B = 2. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
4 |
, B 1+ |
2 |
= 3 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
+ |
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
(1 − 2x)(1 + 4x) |
1− 2x |
1+ 4x |
|
|
|
|
|
||||||||||||||||
|
|
Воспользуемся разложением функции |
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
= 1 |
+ x + x2 + x3 |
|
+ x4 + x5 + … + xn + …, |
|
|
|
||||||||||||||||||||||
|
|
|
|
1 − x |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интервал сходимости x (−1;1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Каждую дробь разложим отдельно: |
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
4 |
|
|
|
5 |
|
|
|
|
n |
|
||||
|
|
|
|
= 1 + 2x + ( |
2x) |
|
|
+ (2x) |
+ ( |
2x) |
|
+ (2x) + … + (2x) |
|
+ …, |
||||||||||||||||
1 − 2x |
|
|
|
|
||||||||||||||||||||||||||
интервал сходимости |
|
2x |
|
<1, − 1 |
|
< x < 1 . |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 2(1 − 4x + (4x) |
2 |
3 |
|
4 |
|
|
|
n |
|
n |
+ …), |
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
− (4x) |
+ (4x) |
|
|
− … + (−1) |
|
(4x) |
|
|
|||||||||||||||||||
|
1 + 4x |
|
|
|
|
|
|
|||||||||||||||||||||||
интервал сходимости |
|
4x |
|
<1, − 1 |
|
< x < 1 . |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Просуммируем ряды, сгруппируем по степеням х:
(1 − 2x)3(1 + 4x) =
= 1 + 2x + (2x)2 + (2x)3 + (2x)4 + (2x)5 + … + (2x)n + …
+2(1− 4x + (4x)2 − (4x)3 + (4x)4 − … + (−1)n (4x)n + …) =
48
= 1 + 2x + (2x)2 + (2x)3 + (2x)4 + (2x)5 + … + (2x)n + …
+2 − 2 4x + 2(4x)2 − 2(4x)3 + 2(4x)4 − … + (−1)n 2(4x)n + … = = 1+ 2x + 22 x2 + 23 x3 + 24 x4 + 25 x5 + … + 2n xn + …
+2 − 23 x + 25 x2 − 27 x3 + 29 x4 − 211 x5 + …(−1)n 22n+1 xn + … =
= 3 + (2 − 23 )x + (22 + 25 )x2 + (23 − 27 )x3 + …(2n + (−1)n 22n+1 )xn + … .
3 |
= (2n + (−1)n 22n+1 )xn . |
|
∞ |
(1− 2x)(1+ 4x) |
n=0 |
Интервал сходимости будет наименьшим из двух интервалов:
− 14 < x < 14 .
2.5. Применение степенных рядов
Степенные ряды используют для приближенного вычисления значения функций, интегралов, решения дифференциальных уравнений и т.д.
Пример 36. Вычислить e2 с точностью до 0,01. Используем разложение
|
|
|
|
e |
x |
= 1 |
+ |
|
x |
+ |
x2 |
|
+ |
x3 |
|
+ |
x4 |
+ |
x5 |
+ … + |
xn |
+ … . |
|
|
|
|
|
|
1! |
2! |
|
3! |
|
4! |
5! |
n! |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
При x = 2 получим числовой ряд: |
|
|
|
|
|||||||||||||||||||
|
|
|
|
e2 = 1 |
+ |
|
2 |
+ |
22 |
|
+ |
23 |
|
+ |
24 |
+ |
25 |
+ … + |
2n |
+ … . |
|
||
1! |
|
|
|
|
|
|
n! |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2! 3! 4! 5! |
|
|
|
|||||||||||
Точность |
|
вычисления |
|
0,01, |
т.е. |
остаток |
ряда |
||||||||||||||||
Sn = |
|
S − Sn |
|
< 0,01, |
|
где |
Sn |
– частичная сумма ряда. Возникает во- |
|||||||||||||||
|
|
|
|||||||||||||||||||||
прос: сколько надо взять слагаемых, чтобы добиться заданной точности? Числовой ряд является знакоположительным, а не знакоче-
49

редующимся, следовательно, нельзя судить о погрешности по величине первого отбрасываемого члена. Выпишем остаток ряда:
|
|
|
Sn = |
|
|
|
2n+1 |
|
|
|
|
|
|
|
2n+2 |
|
|
|
2n+3 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ … = |
||||||||||||||
|
|
|
(n + 1)! |
(n + 2)! |
(n + 3)! |
|||||||||||||||||||||||||||||||||
= |
2n+1 |
|
+ |
|
|
|
|
|
2n+2 |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
2n+3 |
|
|
|
|
+ … = |
||||||
(n + 1)! |
(n + 1)!(n + 2) |
(n + 1)!(n + 2)(n + 3) |
||||||||||||||||||||||||||||||||||||
|
|
|
2n+1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ … . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
(n + 2) |
|
|
|
(n |
+ 2)(n + |
3) |
|
|||||||||||||||||||||
|
|
(n + 1)! |
|
|
|
|
||||||||||||||||||||||||||||||||
Заменим выражения (n + 2) , |
(n + 3),… на (n +1) , тогда зна- |
|||||||||||||||||||||||||||||||||||||
менатель каждой дроби станет меньше, а дробь больше. Получим |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2n+1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
22 |
|
|
|
|
|
||||||||
|
|
S |
|
< |
|
|
|
|
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ … . |
|||||||
|
|
|
|
|
|
|
|
|
(n + 1) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n + 1) |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
(n + 1)! |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
В скобках имеем бесконечно убывающую геометрическую |
||||||||||||||||||||||||||||||||||||||
прогрессию со знаменателем q = |
|
|
2 |
|
|
|
, её сумма |
|||||||||||||||||||||||||||||||
|
(n |
+ 1) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
|
= n + 1. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1− q |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1− |
|
|
|
|
|
|
n − 1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Остаток ряда не превосходит: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
Sn < |
|
|
2n+1 |
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n − 1 = |
|
< 0,01. |
||||||||||||||||||||||||||||||
|
|
|
|
(n + 1)! |
n!(n − 1) |
|||||||||||||||||||||||||||||||||
Получили неравенство для определения n:
(2n ) < 0,01, n! n − 1
или
50
