
книги / Математика. Линейная алгебра, векторная алгебра, аналитическая геометрия-1
.pdf
рам заданных плоскостей |
|
1 = {3; 3;1} и |
|
2 = {2; − 3; − 2}, в ка- |
|||||||||||||||||||||||||||
N |
N |
||||||||||||||||||||||||||||||
честве его можно взять векторное произведение векторов |
|
1 |
|||||||||||||||||||||||||||||
N |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
||||
и |
|
2 : |
|
= |
|
1 × |
|
= |
3 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
N |
S |
N |
N2 |
|
|
|
|
||||||||||||||||||||||||
|
= −3i |
+ 8 j −15k . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
− 3 |
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Таким |
образом, |
l = −3, |
m = 8, |
n = −15. За |
точку |
||||||||||||||||||||||||
M0 (x0 ; y0 ; z0 ), |
через которую проходит искомая прямая, |
можно |
|||||||||||||||||||||||||||||
принять точку ее пересечения с любой из координатных плоскостей, например с плоскостью XOY. Поскольку при этом z0 = 0,
координаты x0 и y0 определяются из системы уравнений заданных плоскостей, если положить в них z = 0.
3x + 3y − 1 = 0, |
|
7 |
|
|
16 |
|
||
|
= 0, |
отсюда получаем x0 = |
|
, y0 |
= − |
|
. |
|
5 |
15 |
|||||||
2x − 3y − 6 |
|
|
|
|
||||
Итак, искомые канонические уравнения прямой имеют вид
x − |
7 |
|
|
y + |
16 |
|
z − 0 |
|
x − |
7 |
|
|
y + |
16 |
|
|
z − 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
|
= |
15 |
= |
или |
5 |
|
= |
15 |
|
= |
. |
||||||
− 3 |
|
|
|
|
|
− 8 |
|
|
||||||||||
|
|
8 |
|
|
− 15 |
3 |
|
|
|
15 |
|
|||||||
Замечание.
В общем случае, точка M0 (x0; y0 ; z0 ) может быть другой.
Задача 5. |
Найти |
|
острый |
|
|
угол |
|
между |
прямыми |
|||||||||||
x − 1 |
= |
y + 5 |
= |
z − 7 |
и |
x − 4 |
= |
y + 5 |
= |
z − 6 |
. |
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
− 6 |
3 |
|
|
|
1 |
2 |
|
|
− 2 |
|
|
|
|
||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По формуле (6) получаем |
|
|
|
|
|
|
|
|
||||||||||||
|
|
cos ϕ = |
|
|
2 1+ (− 6) 2 + 3 (− 2) |
|
(− 2)2 = |
16 |
, |
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
22 + |
(− 6)2 + 32 |
12 + 22 + |
|
21 |
||||||||||||||
т.е. ϕ = arccos16 ≈ 40°. 21
121

Задача 6. Составить уравнение прямой, проведенной через точку M (− 7; 0; 9) перпендикулярно двум данным прямым:
x − 3 = y + 4 = z − 5 , x + 1 = y − 3 = z − 2 . |
|||||
− 2 |
− 1 |
3 |
4 |
6 |
− 5 |
Решение.
Приведем два способа решения задачи.
Способ первый.
Запишем уравнения любой прямой, проходящей через точку M:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 7 |
= |
|
y |
= |
z − 9 |
. |
|
(10) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
m |
|
n |
|
|||||||
|
|
|
Из условия ее перпендикулярности к данным прямым |
||||||||||||||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
− 2l − m + 3n = 0, |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4l + 6m − 5n = 0, |
|
||||||||||||
откуда m = − |
n |
; |
l = |
13n |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
4 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Подставляя |
|
найденные |
|
значения в |
(10), получим: |
|||||||||||||||||||
|
x + 7 |
= |
y |
= |
z − 9 |
или |
x + 7 |
= |
|
y |
= |
z − 9 |
. |
|
|||||||||||||
|
13n |
− |
n |
|
|
|
n |
13 |
|
|
|
− 2 |
8 |
|
|
||||||||||||
|
8 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Способ второй.
x + 7 = y = z − 9 , где S = {l; m; n} – направляющий вектор l m n
искомой прямой. Из условия задачи следует, что
S S1 = {− 2; −1; 3},
S S2 = {4; 6; − 5}.
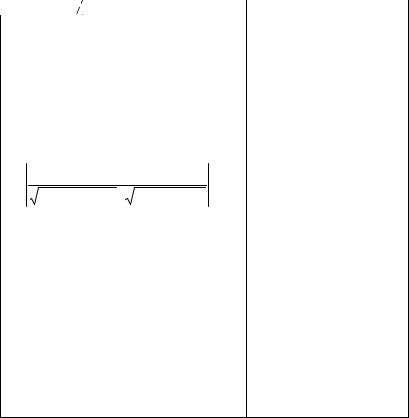
Следовательно, направляющим вектором искомой прямой может быть вектор
122
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
k |
= {− 13; 2; − 8} или |
|
= {13; − 2; 8}. |
||||||||||||||||||
|
|
|
= |
|
|
× |
|
= |
|
− 2 |
− 1 |
3 |
|
|
|||||||||||||||||||||
|
|
S |
S1 |
S2 |
|
S |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
6 |
|
− 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Таким образом, имеем |
|
x + 7 |
= |
y |
|
= |
z − 9 |
|
|
– канонические |
||||||||||||||||||||||
|
|
|
13 |
− 2 |
|
|
|||||||||||||||||||||||||||||
уравнения искомой прямой. |
|
8 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 5. Прямая и плоскость |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Основные формулы и рисунки |
|
|
|
Определения |
||||||||||||||||||||||||||||||
|
|
|
|
и замечания |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1. Острый |
|
угол |
между |
|
прямой Углом ϕ между прямой |
||||||||||||||||||||||||||||||
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
|
и плоскостью |
и плоскостью будем на- |
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
l |
m |
n |
|
|
|
|
|
|
|
зывать |
любой |
|
из двух |
|||||||||||||||||||||
|
Ax + By + Cz + D = 0 определяется по |
смежных углов, образо- |
|||||||||||||||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ванных прямой и ее про- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin ϕ = |
|
|
|
|
|
|
|
екцией |
|
на |
плоскость |
|||||||||||||
|
|
|
|
|
|
|
|
Al + Bm + Cn |
|
|
|
|
(рис. 1). |
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
|
|
|
. (1) |
Замечание. |
|
|
|
|
||||||||||||||||||||||||
A2 + B2 + C2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
l2 + m2 + n2 |
|
Угол α находим из ска- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лярного |
|
произведения |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормального вектора |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости и направляю- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щего вектора |
|
прямой. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
α + ϕ = π , |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
cosα = sin ϕ.
Рис. 1
123
Основные формулы и рисунки |
Определения |
|
|
|
||||||||||||||
и замечания |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
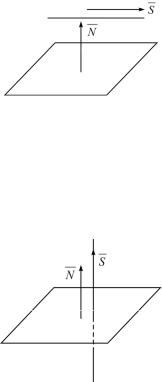
2. Условие |
параллельности |
прямой |
Замечание. |
|
|
|
|
|||||||||||
и плоскости (рис. 2) |
|
Прямая и плоскость па- |
||||||||||||||||
Al + Bm + Cn = 0. |
(2) |
раллельны, если скаляр- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
ное произведение |
на- |
||||||||
|
|
|
|
|
|
|
|
|
правляющего вектора |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
S |
||||||||
|
|
|
|
|
|
|
|
|
прямой |
и |
нормального |
|||||||
|
|
|
|
|
|
|
|
|
вектора |
|
|
|
|
|
плоскости |
|||
|
|
|
|
|
|
|
|
|
|
|
N |
|||||||
|
|
|
|
|
|
|
|
|
равно нулю. |
|
|
|
|
|||||
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||||||
3. Условие перпендикулярности пря- |
Замечание. |
|
|
|
|
|||||||||||||
мой и плоскости (рис. 3) |
|
Прямая и плоскость пер- |
||||||||||||||||
|
|
A |
= |
B |
= |
C |
. |
(3) |
пендикулярны, если на- |
|||||||||
|
|
|
|
|
правляющий вектор |
|
|
|
||||||||||
|
|
l m n |
|
|
S |
|||||||||||||
|
|
|
|
|
|
|
|
|
прямой |
и |
нормальный |
|||||||
|
|
|
|
|
|
|
|
|
вектор |
|
|
|
плоскости |
|||||
|
|
|
|
|
|
|
|
|
|
N |
||||||||
|
|
|
|
|
|
|
|
|
коллинеарны. |
|
|
|
||||||
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4. Условие |
принадлежности |
прямой |
|
|
|
|
|
|
|
|
|
|
||||||
плоскости (рис. 4): |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Al + Bm + Cn = 0, |
(4) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
+ By0 + Cz0 + D = |
|
|
|
|
|
|
|
|
|
|
|||||||
Ax0 |
0. |
|
|
|
|
|
|
|
|
|
|
|||||||
124

Основные формулы и рисунки |
Определения |
|
и замечания |
||
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. Точка пресечения прямой с плоско- Замечание. |
|
|
|
|||||||||||
стью (рис. 1) |
|
|
|
|
|
|
|
Чтобы решить систему |
||||||
x − x0 |
|
|
y − y0 |
|
|
z − z0 |
|
(5), нужно от канониче- |
||||||
|
|
= |
|
|
= |
|
|
, |
ских уравнений прямой |
|||||
l |
|
m |
|
n |
||||||||||
O : |
|
|
|
|
(5) |
|||||||||
|
|
|
+ Cz + D |
= 0. |
|
перейти |
к параметриче- |
|||||||
Ax + By |
|
ским уравнениям: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x |
= x0 + lt, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= y0 + mt, |
(6) |
||
|
|
|
|
|
|
|
|
|
|
y |
||||
|
|
|
|
|
|
|
|
|
|
|
= z0 + nt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
||
|
|
|
|
|
|
|
|
|
Подставляя эти выраже- |
|||||
|
|
|
|
|
|
|
|
|
ния для x, y, z в уравне- |
|||||
|
|
|
|
|
|
|
|
|
ние плоскости, опреде- |
|||||
|
|
|
|
|
|
|
|
|
ляем параметр t: |
|
|
|||
|
|
|
|
|
|
|
|
|
t = − |
Ax0 |
+ By0 |
+ Cz0 |
+ D |
. |
|
|
|
|
|
|
|
|
|
Al + Bm + Cn |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Подставляя |
найденное |
||||
|
|
|
|
|
|
|
|
|
значение |
t в |
уравнение |
|||
|
|
|
|
|
|
|
|
|
(6), получаем координа- |
|||||
|
|
|
|
|
|
|
|
|
ты искомой точки пере- |
|||||
|
|
|
|
|
|
|
|
|
сечения прямой и плос- |
|||||
|
|
|
|
|
|
|
|
|
кости. |
|
|
|
|
|
125

|
|
|
|
Задачи |
|
|
|
|
|
|
|
|
Задача 1. Найти угол между прямой |
x = 9 + t, |
y = 5 − 2t, |
||||||||
z = −1− t |
и плоскостью 4x − 2y + 2z + 7 = 0. |
|
|
|
|
|
|
|
|||
|
Решение. |
|
|
|
|
|
|
|
|
||
|
Запишем уравнения данной прямой в виде |
|
x − 9 |
= |
y − 5 |
= |
|||||
1 |
|
||||||||||
|
|
|
|
|
|
|
|
− 2 |
|||
= |
z + 1 |
. |
Теперь, используя |
формулу (1) |
при |
A = 4, |
|
B = −2, |
|||
|
|
||||||||||
|
− 1 |
|
|
|
|
|
|
|
|
|
|
C = 2, l = 1, m = −2, n = −1, |
получим |
|
|
|
|
|
|
|
|||
|
|
|
4 1 + (− 2) (− 2)+ 2 (− 1) |
|
6 |
|
1 |
|
|||
|
sin ϕ = |
42 + (− 2)2 + 22 |
12 + (− 2)2 + (− 1)2 = |
|
24 |
6 |
= 2 . |
||||
Таким образом, ϕ = π . 6
Задача 2. Составить параметрические уравнения прямой, |
|||
проходящей через точку |
A(− 7; − 3; 2) |
и перпендикулярной |
|
плоскости x − 4y − 5z + 8 = 0. |
Найти точку M прямой, соответст- |
||
вующую значению параметра t = 2. |
|
||
Решение. |
|
|
= {1; − 4; − 5} данной |
Поскольку нормальный вектор |
|
||
N |
|||
плоскости перпендикулярен ей, по условию он должен быть параллелен искомой прямой. Поскольку x0 = −7, y0 = −3, z0 = 2, l = 1, m = −4, n = −5, получаем параметрические уравнения прямой:
x = −7 + t,y = −3 − 4t,
z = 2 − 5t.
126

|
При t = 2 |
находим x = −5, |
y = −11, |
z = −8, |
т.е. получаем |
|||||||||||
точку M (− 5; − 11; − 8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Задача 3. Убедиться в том, что прямая |
x − 2 |
= |
y + 4 |
= |
z − 1 |
|
|||||||||
|
|
|
− 2 |
|||||||||||||
|
|
|
|
|
4 |
|
3 |
|
|
|
||||||
параллельна плоскости 5x − 2y + 7z + 3 = 0. |
|
|
|
|
|
|
|
|
|
|||||||
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании условия (2), где l = 4, |
m = 3, |
n = −2, |
A = 5, |
||||||||||||
B = −2, C = 7, имеем 4 5 + 3 (− 2)+ (− 2) 7 = 0. |
|
|
|
|
|
|
|
|
|
|||||||
|
Задача 4. Найти точку пересечения прямой |
x + 1 |
= |
y − 2 |
= |
|||||||||||
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
= |
z −1 |
с плоскостью 3x − 2y + z − 3 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем |
уравнение прямой в параметрическом |
виде: |
|||||||||||||
x = −1+ 2t, y = 2 + t, z = 1− t. |
Подставляя значения x, |
|
y, z |
|||||||||||||
в уравнение |
плоскости, |
имеем |
3 (− 1+ 2t)− 2 (2 + t)+ |
|||||||||||||
+ (1− t)− 3 = 0 , откуда t = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя теперь это значение t в параметрические уравнения прямой, находим координаты точки пересечения: x = 5,
y = 5, z = −2, M (5; 5; − 2).
Задача 5. Проверить, что прямая x − 2 = y − 3 = z + 1 ле- 2 1 3
жит в плоскости x + y − z − 6 = 0.
Решение.
Здесь x0 = 2, y0 = 3, z0 = −1, l = 2, m = 1, n = 3,
A = 1, B = 1, C = −1, D = −6.
127
Проверим условия (4):
2 1+ 1 1+ (− 1) 3 = 0, 1 2 + 1 3 + (−1) (−1)− 6 = 0.
Условия (4) здесь выполнены, а это значит, что прямая лежит в плоскости.
Задача 6. Дана прямая |
x − 1 |
= |
y |
= |
z + 1 |
и вне ее точка |
|
|
|
||||
2 |
3 |
|
− 1 |
|||
M (1;1;1). Найти точку N, симметричную M относительно дан-
ной прямой.
Решение.
Составим уравнение плоскости, проходящей через точку M, перпендикулярной к данной прямой. 2(x − 1)+ 3(y − 1)− (z − 1) = 0
или 2x + 3y − z − 4 = 0.
Найдем точку Q, в которой эта плоскость пересекает данную прямую. Запишем уравнения прямой в параметрическом
виде: x = 1+ 2t, |
y = 3t, |
z = −1− t. |
|
|
|
|
|
|
|
|
|
|
Подставляя |
x, y, |
z в уравнение |
плоскости, получим: |
|||||||||
2 (1+ 2t)+ 3 (3t)− (−1− t)− 4 = 0, 14t −1 = 0, t = |
1 |
. |
||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
8 |
|
3 |
|
15 |
|
|
|||
Точка Q имеет координаты |
Q |
|
; |
|
|
; − |
|
|
. |
Тогда коорди- |
||
|
|
|
|
|
||||||||
|
|
|
7 |
|
14 |
|
14 |
|
|
|||
наты симметричной точки можно найти из формул координат
середины отрезка, т.е. |
|
= |
|
xM + xN |
; |
|
|
|
= |
yM + yN |
; |
|
= |
zM + zN |
; |
||||||||||||||||||||||||
x |
|
|
y |
z |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
||||||||||||
|
8 |
= |
1+ xN |
; |
3 |
= |
1+ yN |
; − |
15 |
= |
|
1+ zN |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
14 |
|
|
|
2 |
|
|
14 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Откуда |
|
xN |
= |
9 |
; |
|
|
yN = − |
4 |
; |
|
zN |
= − |
22 |
. |
Следовательно, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
7 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|||||||||
|
|
9 |
|
4 |
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
N |
|
; − |
|
; − |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
7 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
128
§ 6. Кривые II порядка
Основные формулы и рисунки |
|
|
Определения |
|
|||||||||||
|
|
и замечания |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
|
|
|
|
|
|
|
|
Эллипс есть |
геометриче- |
|||||
|
|
|
|
|
|
|
|
|
ское место точек, сумма |
||||||
|
|
|
|
|
|
|
|
|
расстояний |
которых |
до |
||||
|
|
|
|
|
|
|
|
|
двух |
данных |
точек |
F1 |
|||
|
|
|
|
|
|
|
|
|
и F2 , называемых фокуса- |
||||||
|
|
|
|
|
|
|
|
|
ми эллипса, есть величина |
||||||
|
|
|
|
|
|
|
|
|
постоянная (большая, чем |
||||||
|
|
|
Рис. 1 |
|
|
расстояние |
между |
фоку- |
|||||||
|
|
|
|
|
сами). |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
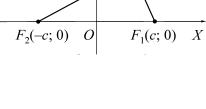
Замечание. |
фокусы |
через |
||||
|
|
|
|
|
|
|
|
|
Обозначим |
||||||
|
|
|
|
|
|
|
|
|
F1 и F2 , расстояние между |
||||||
|
|
|
|
|
|
|
|
|
ними через 2c, а сумму |
||||||
|
|
|
|
|
|
|
|
|
расстояний |
от |
произволь- |
||||
|
|
|
|
|
|
|
|
|
ной точки эллипса до фо- |
||||||
|
|
|
|
|
|
|
|
|
кусов – через 2a (рис. 1). |
||||||
|
|
|
|
|
|
|
|
|
По |
определению 2a > 2c, |
|||||
|
|
|
|
|
|
|
|
|
т.е. |
a > c. |
|
|
|
|
|
2. Каноническое уравнение эллипса |
Уравнение (1) содержит |
x |
|||||||||||||
|
x |
2 |
+ |
y |
2 |
|
=1. |
|
и y только в четных степе- |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
(1) |
|
|
|
|
|
|
|
||||
|
a2 |
b2 |
нях, |
следовательно, |
эллипс |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
симметричен относительно |
||||||
|
|
|
|
|
|
|
|
|
осей OX и OY , |
а также от- |
|||||
|
|
|
|
|
|
|
|
|
носительно точки O(0; 0), |
||||||
|
|
|
|
|
|
|
|
|
которая называется |
цент- |
|||||
|
|
|
|
|
|
|
|
|
ром эллипса. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
129

Основные формулы и рисунки |
|
|
Определения |
|
|||||||
|
|
и замечания |
|
||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Точки A1, A2 , B1 , B2 назы- |
||||||
|
|
|
|
|
ваются вершинами эллипса; |
||||||
|
|
|
|
|
a – большая полуось эл- |
||||||
|
|
|
|
|
липса, b – малая полуось |
||||||
|
|
|
|
|
эллипса (a > b); |
|
|
|
|||
|
|
|
|
|
|
F1, F2 OX (рис. 2). |
|
||||
|
Рис. 2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
3. |
a2 − c2 = b2. |
(2) |
Величины a, b, c связа- |
||||||||
|
|
|
|
|
ны соотношением (2), |
где |
|||||
|
|
|
|
|
2c – расстояние между |
||||||
|
|
|
|
|
фокусами. |
|
|
|
|
||
4. Эксцентриситет эллипса |
|
Эксцентриситет эллипса – |
|||||||||
|
|
c |
|
|
это отношение расстояния |
||||||
|
ε = |
. |
(3) |
между фокусами |
к боль- |
||||||
|
|
||||||||||
|
|
a |
|
шой оси эллипса: |
2c |
|
или |
||||
|
|
|
|
|
|||||||
|
|
|
|
|
2a |
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
c |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Следует |
запомнить, |
что |
||||
|
|
|
|
|
форма эллипса (мера его |
||||||
|
|
|
|
|
сжатия) |
характеризуется |
|||||
|
|
|
|
|
эксцентриситетом ε < 1 (т.к. |
||||||
|
|
|
|
|
0 < c < a ). |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
130
