
книги / Физические теории пластичности
..pdfгде ρ0 – плотность материала, ψ(Rk ) , ψΤ(k ) , ψ(Ρk ) – составляющие свобод-
ной энергии на k-й СС, являющиеся явными функциями соответствующих термодинамических параметров состояния R(k ) , Τ(k ) , Ρ(k ) . Из неравенства Клаузиуса–Дюгема с учетом независимости термодинамиче-
ских параметров |
состояния |
|
R(k ) , Τ(k ) , Ρ(k ) |
непосредственно |
следует |
|||||||||||||||||||||
общий вид эволюционных уравнений для r(k ) , τc(k ) , ρ(k ) : |
|
|
|
|||||||||||||||||||||||
|
(k ) |
|
|
∂ ψi |
|
∂ |
ψ |
(k ) |
(k ) |
|
|
|
∂ |
ψi |
|
∂ |
ψ(k ) |
|
|
|||||||
r |
|
= ρ |
0 |
|
|
= |
|
|
R |
; τc |
= ρ |
0 |
|
|
|
|
= |
|
|
Τ |
; |
|
||||
|
|
(k ) |
|
|
|
|
|
(k ) |
|
|
|
|
||||||||||||||
|
|
|
∂ R |
|
∂ |
R |
(k ) |
|
|
|
|
|
Τ |
∂ |
|
|
Τ |
(k ) |
|
(7.88) |
||||||
|
|
|
|
|
|
|
|
∂ ψi |
|
∂ |
∂ |
|
|
|
|
|
||||||||||
|
|
|
|
|
ρ |
(k ) |
= ρ |
|
|
|
ψ(k ) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
Ρ |
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 ∂ Ρ(k ) |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
∂ Ρ(k ) |
|
|
|
|
|
|
|
|
|||||||||
Далее для построения в рамках термодинамического подхода теории вязкопластичности монокристалла вводится вязкопластический потенциал:
Ω= ∑Ω |
(φ |
(k ) |
), где φ |
(k ) |
= φ |
(k ) |
(τ |
(k ) |
, r |
(k ) |
, τc |
, ρ |
(k ) |
, θ). |
|
ˆ k |
|
|
ˆ |
|
|
(k ) |
|
|
(7.89) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k
С использованием вязкопластического потенциала, пластические деформации реализуются сдвигом по СС, дующее соотношение:
d p = |
∂ Ω |
= ∑ |
∂ Ω∂ |
|
φ(k ) |
= ∑ γ(k )m(k ) . |
|
∂ σ |
|
|
|||||
|
k ∂ φ(k ) ∂ σ |
k |
(S) |
||||
учитывая, что получают сле-
(7.90)
Суммирование в записанных выше соотношениях осуществляется по всем активным системам скольжения.
Функция диссипации Ф определяется разностью между мощностью работы напряжений на пластических деформациях и мощностью работы на квазистатическом (или вязком) и кинематическом упрочнении, чему соответствуют два представления функции диссипации:
|
p |
|
|
|
|
∂ ψi ∂ ψΤ(l) |
||
Φ= σ:d |
|
– ∑ |
∑ρ |
|
|
|
|
|
|
0 ∂ ψ(l)∂ Τ(k ) |
|||||||
|
|
k |
|
l |
||||
|
|
|
|
|
|
Τ |
||
|
|
∑ρ0 |
|
|
Τ(k ) – ∑ |
||
|
|
l |
∂ |
|
k |
|
|
∂ ψi ∂ ψ(Ρl) |
(k ) |
|
|||
|
|
|
Ρ |
|
, (7.91) |
ψ(l∂) |
Ρ(k ) |
|
|||
Ρ |
|
|
|
|
|
171
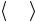
|
|
|
i |
|
|
(l) |
|
Φ= σ:dp – ∑ |
∑ρ |
|
∂ ψ |
|
|
∂ ψR |
|
0 |
∂ ψR |
∂ |
|
||||
k |
l |
R |
(k ) |
||||
|
|
(l) |
|
|
|
||
R(k )
– ∑ ∑ρ∂
0 k l
∂ ψi ∂ ψ(Ρl) |
(k ) |
|
|
|||
|
|
|
Ρ |
|
. |
(7.92) |
ψ(l∂) |
Ρ(k ) |
|
||||
Ρ |
|
|
|
|
|
|
Относительно соотношения (7.91) необходимо отметить следующее: по сути дела, считается, что часть энергии не диссипирует, а запасается в виде внутренней энергии упругих искажений решетки, энергии взаимодействующих дислокаций, что и описывают 2-й и 3-й члены правой части. Соотношение (7.92) в этом смысле менее понятно: как правило, вязкостное трение приводит к рассеянию энергии; вероятно, в данном случае следует помнить о вязкопластичности, т.е. повышение вязкого сопротивления приводит к повышению запасенной упругой энергии, реализуемой при разгрузке.
Приведенная формулировка модели, обозначаемая как ЕВ-модель (E. Busso), далее сопоставляется с другими известными соотношениями пластичности монокристаллов. В рассмотрение включены модели
G. Calletaud и L. Meric e.a. (обозначенные как GC), L. Anand с соавторами (LA), D. McDowell&R. McGinty (DM). Все указанные модели отно-
сятся к классу упруговязкопластических, однако в рамках моделей GC и LA рассматриваются также варианты с исключением вязких членов. В табл. 7.1 и 7.2 приведена достаточно полная информация обо всех соотношениях анализируемых моделей. В табл. 7.1 приведены функции, описывающие вязкопластичность, выражения составляющих свободной энергии, соотношения для сопряженных термодинамических переменных, характеризующих различные виды упрочнения. В табл. 7.2 содержатся сведения об эволюционных уравнениях для критического напряжения сдвига, вязкого сопротивления и остаточных микронапряжений.
Реализация всех рассматриваемых моделей осуществлялась с использованием МКЭ и неявной схемы интегрирования по времени. Сопоставление результатов расчета осуществлено для ГЦК-монокристаллов (12 потенциально активных систем скольжения). Идентификация параметров модели проводилась для случая одноосного нагружения по направлению 100 при квазистатическом нагружении и использовании закона уп-
рочнения Тейлора. Калибровка проводилась таким образом, чтобы влияние вязкостных членов в интервале скоростей деформации 10–1–10–3 с–1 было весьма малым. Во всех моделях при калибровке пренебрегалось кинематическим упрочнением (т.е. ρk = 0 ). Все коэффициенты моделей сведены в табл. 7.3.
172

Таблица 7.1 Функции, используемые в моделях пластичности кристаллов
Функции |
|
|
|
|
|
GC |
|
|
|
|
|
|
|
|
|
|
EB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LA |
|
|
|
|
|
|
|
|
|
|
|
DM |
|
|
|
|
|
|||||||||||
|
f (k) |
|
|
|
τ(k ) − ρ(k ) |
|
− τc( k ) − τc0 |
|
|
|
τ( k ) − ρ( k ) |
|
− τc( k ) |
|
|
|
|
|
|
τ( k ) − ρ( k ) |
|
|
|
|
τ( k ) − ρ( k ) |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
γ |
( k ) |
|
|
|
γ0 |
|
f |
k |
τˆ0 |
n |
|
γ0 |
|
− |
F0 |
1 − ( |
f |
( k ) |
ˆ |
) |
p |
q |
γ0 |
|
f |
(k) |
r |
(k) n |
γ0 f |
(k ) |
r |
(k ) n |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ex p |
|
|
|
|
|
|
τ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ψR {R |
|
} |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
1 |
|
|
hτ (R |
|
|
) |
2 |
|
|
1 |
hτ (R |
|
|
) |
2 |
|
|||||||||||||||
ˆ |
(k) |
|
(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
(k) |
|
|
|
|
|
(k ) |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
1 |
|
hτ (T |
|
|
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
{T |
|
} |
|
1 |
|
τc |
|
hτ |
|
∑l h T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|||||||||||
ψT |
(k ) |
|
|
|
|
l |
|
|
|
|
|
|
(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
(k ) |
|
|
|
|
2 |
(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ψP {P |
|
} |
|
|
1 |
hR |
(P |
|
) |
2 |
|
|
|
|
|
1 |
|
hR (P |
|
|
) |
2 |
|
|
|
|
1 |
|
hR (P |
|
|
|
) |
2 |
|
1 |
|
hR (P |
|
|
) |
2 |
|||||||||||||||||||
ˆ |
(k) |
|
(k) |
|
|
|
|
|
|
|
|
( k ) |
|
|
|
|
|
|
|
|
|
|
( k ) |
|
|
|
|
|
|
|
|
|
|
|
|
( k ) |
|
|
|
|
|
( k ) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
r (k) |
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
h R( k ) |
|
|
|
|
|
|
|
|
h R( k ) |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
τc( k ) |
|
|
|
|
hτ ∑l hklT (l ) |
|
|
|
|
|
|
|
hτ T ( k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|||||||||||||
|
ρ(k ) |
|
|
|
|
|
|
hρR(k ) |
|
|
|
|
|
|
|
|
|
hρR(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
hρR(k ) |
|
|
|
|
|
|
|
|
hρR(k ) |
|
|
|
|
|||||||||||||||||
Таблица 7.2 Эволюционные уравнения для различных моделей
Модель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение |
|
|
|
|
|
|
|
||||||||||
(k ) |
= |
∑l |
h |
kl |
|
− dτT |
(l ) |
|
γ |
(l ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
τc (GC) |
|
hτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
τ(k ) |
= |
∑l |
h |
kl |
(hτ |
|
|
|
(l ) |
|
|
|
|
|
|
γ |
(l ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
c (EB) |
|
|
− dτ τc |
|
|
− τ0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r(LA)(k ) |
= |
|
|
|
+ (1− qh )δ |
kl |
{1 |
− |
r(l ) |
r } |
a |
|
γ |
(l ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
∑l hτ qh |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
r(DM)(k ) |
= |
|
q h |
|
γ(l ) |
|
− (q |
h |
−1)h |
|
γ(l ) |
|
|
− d r(l ) |
q |
|
γ(l ) |
|
− (q |
−1) |
|
γ(l ) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
∑l |
|
h |
τ |
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
τ |
|
|
|
∑l |
h |
|
|
|
h |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ρ(k ) = |
h si g n(γ( k ) ) − d |
ρ(k ) |
|
γ(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты расчета кривой σ – ε при растяжении ГЦК-моно- кристалла в направлении [1 0 0] при скорости деформации 10–3 с–1 для всех четырех вязкопластических моделей обнаруживают удовлетворительное соответствие.
Анализируются результаты расчетов с использованием указанных вязкопластических моделей при двухосном деформировании монокристаллов. Кристаллографическое направление [1 0 0] совпадает во всех численных экспериментах с одной из осей главных деформаций Х1. Для
173

Таблица 7.3
Материальные параметры анализируемых моделей
|
|
Параметры |
|
Параметры |
|
|||
|
|
|
упругопластических |
|
||||
Параметр |
вязкопластических моделей |
Единицы |
||||||
|
|
|
|
|
моделей |
|
|
|
|
GC |
EB |
LA |
DM |
GC |
|
LA |
|
C11 |
250 |
250 |
250 |
250 |
250 |
|
250 |
ГПа |
C12 |
200 |
200 |
200 |
200 |
200 |
|
200 |
ГПа |
C44 |
100 |
100 |
100 |
100 |
100 |
|
100 |
ГПа |
γ0 |
1,0 |
150 |
7,3 10–4 |
1,0 |
– |
|
– |
с–1 |
n |
2,0 |
– |
0,01 |
0,01 |
– |
|
– |
– |
τ0 |
20 |
465 |
– |
– |
– |
|
– |
МПа |
F0 |
– |
48,9 |
– |
– |
– |
|
– |
КДж моль |
p |
– |
0,163 |
– |
– |
– |
|
– |
– |
q |
– |
1,220 |
– |
– |
– |
|
– |
– |
τc 0 |
100 |
105 |
103 |
108 |
100 |
|
– |
МПа |
r0 |
– |
– |
103 |
108 |
– |
|
100 |
МПа |
r* |
– |
– |
195 |
– |
– |
|
235 |
МПа |
a |
– |
– |
0,929 |
– |
– |
|
1,6 |
– |
hτ |
1008 |
1150 |
1824 |
2203 |
1092 |
|
1953 |
МПа |
dτ |
84 672 |
12,1 |
– |
10,5 |
9532 |
|
– |
– |
hρ |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
0,0 |
МПа |
dρ |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
0,0 |
– |
hkl , qh (активное) |
0 |
0 |
0 |
0 |
0 |
|
0 |
– |
|
|
|
|
|
|
|
|
|
hkl , qh (Тейлор) |
1 |
1 |
1 |
1 |
1 |
|
1 |
– |
|
|
|
|
|
|
|
|
|
реализации моделей используется МКЭ (пакет Zebulon) с элементами, допускающими независимое задание нормальных и сдвиговых деформаций. Исследовались нагружения по лучевым траекториям деформа-
ции |
(двумерный вариант) при отношениях |
ε11 / ε22 = −0, 95… 5, 33 |
|
и ε |
/ ε = 0, 02… 0, 40 (при неизменной скорости деформации ε = 10−2 |
с–1 |
|
11 |
12 |
11 |
|
во всех вариантах). Опыты на двухосное растяжение-сжатие осуществ-
лялись |
|
при использовании изотропного |
закона |
упрочнения Тейлора |
( hkl = q |
h |
= 1, 0 ), сопоставление проведено для траекторий напряжений |
||
|
|
|
|
|
σ11 – σ22 . Результаты расчетов по всем |
четырем |
моделям находятся |
||
в удовлетворительном соответствии. Рассмотрена также активация сис-
тем скольжения и накопленный на них сдвиг; |
для варианта |
ε11 / ε22 = 5, 33 отмечается, что при напряжении σ11 ≈ 250 |
МПа из мно- |
174
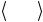
жества СС {1 1 1} 1 1 0 активировались четыре первичные системы скольжения, а при напряжении σ11 ≈ 310 МПа – дополнительно четыре
вторичные СС.
В экспериментах на растяжение-сдвиг использовались оба закона упрочнения – Тейлора и деформационного ( hkl = qh = 0, 0 ). Здесь отме-
чается существенное отличие результатов, полученных, с одной стороны, с помощью моделей EB и GC, с другой – LA и DM; в двух последних при напряжениях σ11 ≈ 210 и 350 МПа соответственно резко акти-
визировались вторичные СС. Данное обстоятельство связано с тем, что в моделях LA и DM учтен разворот кристаллической решетки, что отсутствует в моделях EB и GC. Для проверки этой гипотезы были проведены расчеты с использованием модели DM, в которой были отключены повороты; результаты оказались близки к результатам моделей EB и GC. Сопоставлялись также накопленные сдвиги, результаты аналогичны: близость данных по моделям EB и GC и их резкое отличие от полученных с помощью моделей LA и DM. Отмечается также, что возможным источником различия результатов являются использованные в моделях различные схемы решения нелинейных уравнений, основанные на методе Ньютона–Рафсона; исследованию данного вопроса авторы собираются посвятить будущие работы.
Аналогичное сопоставление осуществлено для всех пяти программ нагружения при использовании упругопластических моделей LA и GC. Во всех расчетах принят закон упрочнения Тейлора ( hkl = qh = 1, 0, ρ(k ) = 0 ).
Для случая двухосного растяжения-сжатия траектории нагружения σ11 – σ22 оказываются близкими; кроме того, обнаруживается их малое от-
личие от траекторий, полученных с помощью вязкопластических моделей LA и GC. Для варианта ε11 / ε22 = 5,33 приведены результаты расчета сум-
марной скорости сдвигов как функции напряжения σ11 и времени. Для обеих моделей при σ11 ≈ 270 и 285 МПа наблюдаются осцилляции сум-
марной скорости сдвига, что авторы связывают с неустойчивостью алгоритма в окрестности точек активизации вторичных СС. Проведено также сопоставление номеров четырех первичных и вторичных активируемых систем скольжения и накопленных сдвигов на них; за исключением нагружения по траектории ε11 / ε22 = −0, 95 , где в модели GC не активирова-
лась ни одна из вторичных систем; соответствие результатов следует при-
175

знать удовлетворительным, учитывая некоторое отличие траекторий нагружения (в модели LA в отличие от модели GC напряжение σ11 достига-
ло в момент активизации вторичных СС нулевого значения). Аналогичное удовлетворительное соответствие получено для программ нагружения рас- тяжение-сдвиг.
Весьма подробно вопросы построения и применения физических моделей упруговязкопластичности для описания поведения поликристаллов в широком диапазоне скоростей деформации (10–3–102 с–1) при больших деформациях (порядка 100 %) и относительно низких гомологических температурах (Тг < 0,3) рассмотрены в статье [68]. Как и в большинстве рассмотренных выше работ, использовано мультипликативное разложение градиента места и ОС анизотропной гиперупругости (с учетом температурной деформации), в котором в качестве мер напряженного и деформированного состояния приняты соответственно второй тензор Пиола–Кирхгоффа и тензор деформаций Коши–Грина, определенные в терминах разгруженной конфигурации.
Пластическое деформирование полагается реализующимся скольжением краевых дислокаций; следует отметить, что, как и во многих других работах последнего десятилетнего периода, закон вязкопластичности выводится на основе уравнения Орована:
γ(k ) = ρ(mk ) bv(k ) (τ(k ) , τc(k ) , θ), ∑ , |
(7.93) |
k |
|
где ρ(mk ) – плотность мобильных дислокаций, v(k ) – средняя скорость движения дислокаций в k-й СС, причем v(k ) равна нулю при τ(k ) < τ(ck ) .
Критическое напряжение сдвига полагается равным сумме двух составляющих: сопротивления близкодействующих барьеров, которые могут быть преодолены за счет термических флуктуаций даже при напряжениях ниже барьера Пайерлса–Набарро (называемого термической составляю-
щей) τ(ctk ) и сопротивления дальнодействующих барьеров (называемого
атермической составляющей) |
τca(k ) |
(см., например, [93]). Для модуля сред- |
||||||||||||
ней скорости движения дислокаций принимается соотношение: |
||||||||||||||
|
|
|
|
|
0 |
|
|
|
(∆τ |
|
|
) |
∆τ(k ) ≤ 0, |
|
|
v |
(k ) |
|
= |
|
|
ψ |
(k ) |
(k ) |
, τct |
(7.94) |
|||
|
|
|
|
|
|
|
|
(k ) |
|
|
|
|||
|
|
|
|
l(k ) νexp |
− |
|
|
|
|
|
|
|
0 < ∆τ(k ) < τct(k ) , |
|
|
|
|
|
|
|
κ θ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
176

где ∆τ(k ) = τ(k ) – τ(cak ) , l(k ) – средняя длина свободного пробега дислока-
ций, ν – характеристический частотный параметр (порядка 1012 с–1), ψ(k ) – свободная энтальпия активации (или свободная энергия актива-
ции Гиббса); направление движения совпадает с направлением сдвиговых напряжений. Предлагается модификация закона упрочнения, рассмотренного выше [64], для учета влияния температуры и скорости деформации.
Для определения макронапряжений используется процедура осреднения Тейлора по представительному объему, включающему 400 зерен. Предлагаемая модель встроена в конечно-элементный пакет ABAQUS. Подробно описаны процедура и результаты идентификации модели, выполненной для чистого (99,987 %) алюминия и алюминиевого сплава (ГЦК-решетка). Для идентификации использованы известные в литературе экспериментальные данные по одноосному растяжению образцов при нескольких значениях постоянных скоростей деформаций и температур. Полученные параметры были далее приняты для теоретического предсказания поведения материала при одноосном нагружении со скачками по скорости деформаций и температуре; режимы изменения скоростей деформаций и температур выбраны аналогичными реализуемым в известных из литературы экспериментах. Сравнение расчетных и экспериментальных данных по зависимостям «напряжение – деформация» показывает хорошее соответствие.
Одним из недостатков моделей поликристаллов, основанных на физических теориях, является необходимость рассмотрения большого количества (сотни и тысячи) зерен со своими ориентациями, что требует существенных затрат процессорного времени. Возможным вариантом уменьшения вычислительных затрат является модель «текстурных компонентов», представленная в статье [75]. Под текстурным компонентом понимается ориентация кристаллической решетки, для которой функция распределения ориентаций (ФРО) имеет локальный максимум. Вместо расчетов для большого числа зерен рассматриваются несколько (в данной работе – пять, четыре из которых соответствуют указанным локальным максимумам ФРО, пятый характеризует распределение остальных ориентаций) элементов («псевдозерен»). Для каждого из псевдозерен используется модель упруговязкопластичности со степенным законом течения и изотропным законом упрочнения. Для аппроксимации ФРО
177
вблизи текстурных компонент принят закон распределения Мизеса– Фишера. Вычисления искомых параметров (скоростей пластических деформаций и напряжений) производятся далее для текстурных компонентов, после чего осуществляется ориентационное осреднение параметров с локальными ФРО. На двух примерах для ГЦК-поликристаллов показано удовлетворительное соответствие результатов, полученных с помощью предлагаемой модели (5 элементов) и модели Тейлора (1000 зерен).
Модификация упруговязкопластической модели, учитывающая поврежденность материала, предложена в [152]. Классическое мультипликативное разложение градиента места дополнено составляющей, отвечающей за порообразование и переводящей пластически деформированную конфигурацию в разгруженную. Приведены кинетические уравнения, описывающие эволюцию пор, связанную с наличием начальных пор, образованием пор от включений вторичной фазы и коалесценцией. Скорости сдвигов по СС определяются степенным законом; использован гиперупругий закон, связывающий тензор деформаций Коши–Грина и второй тензор Пиола–Кирхгоффа, определенные в разгруженной конфигурации. Для случая одноосного нагружения проанализировано влияние ориентации монокристаллических зерен на процесс накопления поврежденности и кривые «напряжение – деформация». Для поликристаллического агрегата меры напряженного и деформированного состояния определяются осреднением по объему; сопоставление кривых σ–ε при растяжении поликристаллического образца для трех алюминиевых сплавов обнаруживает хорошее соответствие экспериментальным данным.
Результаты применения упруговязкопластической модели для анализа особенностей деформирования двухфазного сплава (титан + алюминий) содержатся в статье [134]. Подробно рассмотрены физические механизмы деформирования и упрочнения двухфазного сплава, основной объем которого составляет α-фаза с ГПУ-решеткой, остальная часть имеет слоистую структуру из α + β-фаз (β-фаза – кристаллиты с ОЦКрешеткой). Анализируется деформирование представительного объема поликристаллического агрегата; для решения на макроуровне использован пакет ABAQUS. Особое внимание уделяется идентификации физической модели, для чего авторами осуществлены три серии численных экспериментов.
Модели обобщенных континуумов (в особенности – градиентные теории) все чаще применяются исследователями в последние годы для модификации различных физических теорий. Остановимся детальнее на
178

некоторых работах данного направления. В статье [161], основанной на феноменологической градиентной теории пластичности [92], рассматривается вариант градиентной физической теории упруговязкопластичности. Анализируется случай малых градиентов перемещений, в связи с чем не делается различия между отсчетной и актуальной конфигурациями. В духе микроморфного континуума Миндлина вводятся радиу- сы-векторы макроточки Х и микроточки х, соответствующие операторы Гамильтона обозначаются как и . Каждой макроточке Х приписывается микрообъем δV, наделенный микроструктурой (системами скольжения). Скорости сдвига по произвольной k-й СС определяются разложением в ряд Тейлора с сохранением градиентов первого порядка:
|
γ(k ) (X, x) = |
γ(k ) |
(X) + x γ(k ) (X) , |
(7.95) |
где |
γ(k ) (X) – осредненная |
по |
δV скорость сдвига |
по k-й СС, |
γ(k ) |
(X) – осредненный по δV градиент скорости сдвига по k-й СС. |
|||
Пластическая составляющая тензора деформации скорости далее определяется обычным соотношением:
|
|
|
d p ≡ d′p |
= ∑ γ(k ) (X, x) m(S)(k ) . |
|
|
(7.96) |
|
|
|
|
|
k |
|
|
|
|
|
Подстановка (7.95) в (7.96) и запись мощности напряжений в едини- |
|||||||
це объема на скоростях пластических деформаций, N p = |
1 |
∫ σ: d p dV , |
||||||
δV |
||||||||
|
|
|
|
|
δV |
|
||
приводят к следующему результату: |
|
|
|
|||||
|
|
|
N p = σ : d p + τ • ηp , |
|
|
(7.97) |
||
где |
d p |
= ∑ γ(k ) |
(X) m(S)(k ) , |
ηp = ∑m(S)(k ) γ(k ) (X) , σ |
= |
1 |
σdV , |
|
|
|
k |
|
k |
|
δV δ∫V |
||
τ = |
1 |
∫ σ x dV , |
A •B = Aijk Bijk ; тензор (третьего ранга) |
τ |
называет- |
|||
|
δV |
δV |
|
|
|
|
|
|
ся тензором «парных напряжений».
179

Тензор скорости полных микродеформаций в δV полагается линейной функцией микрокоординат х. Тогда мощность напряжений на единицу объема можно представить соотношением:
|
N = |
1 |
∫ σ: d dV = σ : d + τ • η , |
(7.98) |
|
|
|
δV |
δV |
|
|
где d = 1 |
∫ d dV , |
η = 1 |
∫ d dV . В дальнейшем полагается, что |
||
δV |
δV |
|
δV |
δV |
|
осредненный по δV тензор скорости микродеформаций |
d равен тензо- |
||||
ру скорости макродеформаций D в точке Х, D (Х) = |
d , а d = η . |
||||
Уравнения равновесия и статические граничные условия макроуровня получены на основе принципа виртуальной мощности. В качестве определяющих соотношений макроуровня использован закон Гука в скоростной форме как для напряжений, так и для парных напряжений:
σ = Π: De , τ = le2 Π: ηe , |
(7.99) |
где lе – параметр, имеющий размерность длины и связанный с размером области δV («упругий масштаб»), Π – обычный тензор упругих характеристик (4-го ранга).
На микроуровне используется модифицированная модель вязкопластичности. С этой целью вводятся эффективная скорость сдвига и эффективные сдвиговые напряжения для каждой СС, включающие в себя соответственно градиенты скоростей сдвигов и парные напряжения, с помощью масштабных коэффициентов приведенные к размерности скорости сдвига и обычного напряжения. Закон упрочнения по СС определяется в терминах эффективной скорости сдвига. Принимается степенной закон зависимости эффективной скорости сдвига от эффективного сдвигового напряжения на каждой СС. Модель замыкается гипотезой о равенстве отношений средних по СС скоростей сдвигов и их градиентов (последние умножаются на масштабные факторы) и соответствующих энергетически сопряженных силовых факторов на каждой СС, причем это отношение равно отношению эффективной скорости сдвига к эффективному напряжению сдвига в каждой СС. Приведены результаты решения модельной плоской задачи о деформировании бик-
180
