книги / Строительная механика, динамика и устойчивость композитных конструкций

Проделав подобную процедуру для оставшихся геометрических соотношений, можно убедиться, что возмущенное поле деформаций в теле можно представить как

Для упрощения анализа задачи устойчивости примем ряд допущений (или гипотез):

1. Начальное состояние описывается уравнениями линейной теории упругости. Следовательно:

61

Выражения аналогичны линейной части уравнений (1.9.2.2) для возмущенного поля перемещений u1 .

Подставим соотношение (1.9.2.3) в выражение для полной потенциальной энергии системы в новом, смежном с начальным состоянием. При этом полную потенциальную энергию предста-

62

вим в виде разложения по степеням малого параметра, ограничиваясь линейным и квадратным слагаемыми

где Э0 – полнаяпотенциальная энергиявстационарном состоянии. Если рассматривать слагаемое {u1} как вариацию поля перемещений, то слагаемое Э1 (линейное слагаемое разложения по α) по определению будет вариацией потенциальной энергии

стационарного состояния Э1 Э0 .

В свою очередь приращение потенциальной энергии при переходе из начального равновесного состояния в смежное бесконечно близкое состояние равно

где {q} – объемные силы; {p} – поверхностные силы; V – объем тела; S – поверхность, на которой действуют нагрузки.

A2 0 , и, следовательно, в величину Э2 консервативные си-

лы не входят, а входят только коэффициенты при 2 в выражении для энергии упругого деформирования U.

Таким образом

где [С] – матрица жесткости упругого материала.

63

Учитываяусловиеустойчивости, упругая системаприметвид

где 0 C 0 – поле начальных напряжений.

Энергетический критерий устойчивости вида (1.9.2.12) известен как условие устойчивости Брайана.

1.9.3.Энергетический критерий устойчивости

вформе Тимошенко

где α – малая величина. Деформации, соответствующие возмущенному состоянию, определим, ограничившись квадратичными слагаемыми

Если принять гипотезу о справедливости линейной задачи теории упругости для невозмущенного состояния и пренебречь влиянием изменения размеров и формы конструкции до потери

устойчивости, то для векторов 0 и будут справедливы геометрические соотношения Коши (аналогично подходу Брайана), а компоненты тензора деформаций свяжем с полем пе-

ремещений u2 нелинейными геометрическими соотношениями. Подсчитывая значение приращения энергии (с точностью до

постоянного множителя 2 ), получим

64

Используя условие взаимности работ, можно второе слагаемое представить в виде

где C и, применяя формулу Остроградского – Гаусса,

перейдем к интегралу по поверхности S. При этом на части контура S1 , где заданы граничные условия в напряжениях

u2 T p S – критерий в форме Тимошенко.

S

В отличие от критерия Брайана, критерий устойчивости (1.9.3.6) не содержит начального поля напряжений 0 , но тре-

бует определения поля дополнительных перемещений u2 ,

удовлетворяющего кинематическим граничным условиям и обеспечивающего условие стационарности Э0 0 .

1.10. Устойчивость стержней

Получим условие устойчивости прямолинейного упругого стержня на основе критерия Брайана (рис. 1.18).

65

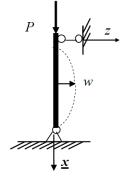
Гипотезы:

1.Ось ненагруженного стержня идеально прямая.

2.Изменением размеров стержня до потери устойчивости пренебрегаем.

3.Изгиб стержня (смежная форма равновесия) описываем в рамках линейной теории изгиба.

В этом случае возмущенное состояние стержня определяется функцией прогиба

в виде дифференциального уравнения проварьируем функционалЭ по w:

66

Первое слагаемое интегрируем дважды по частям, а второе один раз

– дифференциальное уравнение устойчивости стержня.

1.11. Устойчивость анизотропных пластин

На основе энергетического подхода сформулируем критерий устойчивости пластины.

Основные гипотезы:

1.До нагружения пластина плоская и не описывается соотношениями теории упругости.

2.Изменением размеров пластины до потери устойчивости пренебрегаем.

3. Изгиб пластины (возмущенное состояние) описываем в рамках теории изгиба пластин Тимошенко.

Перемещение произвольной точки пластины в пространстве xyz определяется при изгибе по кинематической модели Тимошенко

67

Брайана следующие выражения:

В учитываем только прогиб w.

Распишем выражение для приращения полной энергии для ортотропной пластины (x, y – оси ортотропии):

68

Неизвестные функции w, 1 , 2 и не зависят от z, что позволя-

ет провести интегрирование по координате z с пределами h2 ,

где h толщина пластины, и перейти к интегралам по срединной поверхности S.

сткость; Nx0 , Ny0 , Nxy0 мембранные усилия в пластине в невозму-

щенном состоянии; ( Э) 0 критерий устойчивости пластины.

Если для вариационного уравнения устойчивости пластины поставить систему уравнений Эйлера – Остроградского, то можно перейти к дифференциальной постановке задачи устойчивости пластины.

Так как подынтегральная функция в функционале Э является квадратичной, относительно неизвестных функций и их частных производных, то уравнения Остроградского будут линейными дифференциальными уравнениями в частных производных.

69

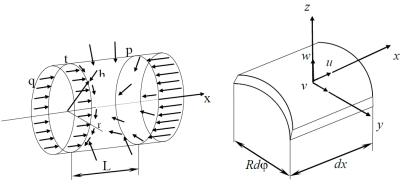
1.12. Устойчивость анизотропных оболочек

Задачу устойчивости тонких упругих оболочек рассмотрим

70