книги / Строительная механика, динамика и устойчивость композитных конструкций

силы на ось z:

Составим уравнения равновесия для моментов относительно осей α, β, z. Уравнение моментов относительно оси α:

Уравнение моментов относительно оси β аналогично, а относительно оси z

161

Это однородные граничные условия, для неоднородных условий на краю заданы какие-либо ненулевые функции. Для замкнутых оболочек часть граничных условий может заменяться условиями периодичности.

7. Энергия упругого деформирования оболочки

используем далее закон Гука, геометрические соотношения и интегрирование по координате z.

4.2. Оболочка вращения

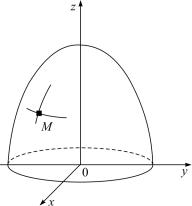
Оболочки вращения осесимметричны, их координатная поверхность представляет собой поверхность вращения (рис. 4.7).

Рис. 4.7. Оболочка вращения

1. Геометрические соотношения. Пересечение плоскости,

которой принадлежит ось z, с координатной поверхностью образует меридиональную кривую (меридиан). Пересечение плоскости, ортогональной оси z, с координатной поверхностью образует окружность, называемую параллелью. Набор меридиональных кривых и параллелей определяет два семейства координатных

162

линий осесимметричной оболочки. Геометрия оболочки вращения определяется формой меридиана.

Рассмотрим оболочку в системе цилиндрических координат r, φ, z (рис. 4.8). Точки поверхности вращения определяются значениями г и р, координата z не является независимой z = z(r). Определим параметры Ламе, когда α – меридиональное и β – окружное направления:

ds rd H d .

Рис. 4.8. Оболочка вращения в цилиндрической системе координат

Определим главные кривизны поверхности вращения: R1 – радиус кривизны меридиана,

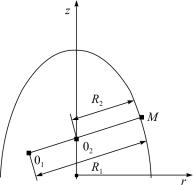
Для определения радиуса кривизны R2 необходимо рассмотреть треугольник O1O M и O2O M , эту геометрическую задачу предлагается решить самостоятельно (рис. 4.9).

163

Кроме того, в соответствии с моделью С.П. Тимошенко нормаль поворачивается в плоскости rz:

и, следовательно, тангенциальные деформации в геометрических соотношениях (4.2.6)–(4.2.7) останутся без изменений, а изгибные деформации примут вид

Тогда тензор обобщенных деформаций будет содержать четыре нулевые компоненты: r , , r , , определяемые через две

функции перемещений u и v.

165

3. Физические соотношения. Обобщенный закон Гука для оболочки вращения запишется, как и в общем случае, с использованием матрицы обобщенных жесткостей, но количество ненулевых компонент тензора обобщенных нагрузок будет меньше; например, в случае технической теории оболочек вращения соотношения примут вид:

4.Энергия упругого деформирования оболочки вращения.

Врамках модели Кирхгофа – Лява

5. Уравнения равновесия оболочки вращения. Рассмотрим оболочку, напряженное состояние которой осесимметрично. Составим уравнения равновесия для элемента оболочки (рис. 4.10).

Спроецируем усилия на нормаль к площадке:

166

в преобразовании выражения было использовано вспомогательное равенство:

Рис. 4.10. Усилия и моменты, действующие на элемент срединной поверхности оболочки вращения

167

Уравнение для моментов составляем относительно оси, касательной к окружности,

Полученных уравнений достаточно для описания деформирования оболочки вращения. Например, в модели С.П. Тимошенко величины N , N , M , M ,Q выражаются через перемещения u, w

иугол поворота 1 , и решается система относительно этих трех функций. В модели Кирхгофа – Лява величины N , N , M , M вы-

ражаются через u, w, и система разрешается относительно u, w,Q .

Для определения искомого решения система полученных обыкновенных дифференциальных уравнений дополняется соответствующими граничными условиями

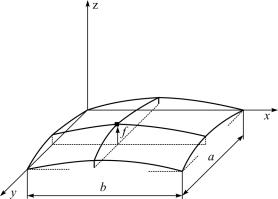
4.3. Пологие оболочки

Пологой оболочкой называется оболочка, геометрия которой может быть отождествлена с геометрией ее проекции на плоскость (рис. 4.11), а, b – характерные размеры проекции, f (x, y) –

функция, описывающая координатную поверхность, т.е. стрела подъема оболочки.

Рис. 4.11. Пологая оболочка

168

Пологими считаются оболочки, для которых выполняется неравенство

В дальнейшем будем рассматривать прямоугольные в плане оболочки.

1. Геометрия оболочки. Так как оболочка пологая, то система координат α, β совпадает с системой координат х, у (см. рис. 4.11) и выражение для квадрата длины дуги

и являются малыми величинами. Следовательно, гауссова кривизна

поэтому пологие оболочки называют оболочками с нулевой гауссовой кривизной.

2. Геометрические соотношения. Учитывая, что выполняют-

169

В последних двух уравнениях пренебрегаем слагаемыми u

R2

сдвиг существенного влияния.

Компоненты тензора деформации оболочки в произвольной точке оболочки на расстоянии z от координатной поверхности

Таким образом, компоненты тензора деформаций eij выра-

жаются через функцию прогиба w, тангенциальные смещения координатной поверхности и, v и углы поворота нормали 1 и 2 .

170