
книги / Строительная механика, динамика и устойчивость композитных конструкций
..pdfгде Ui ,Vi – мембранные усилия; Wi , M xi , M yi – изгибающие уси-
лия. Таким образом, для конечного элемента определим вектор размерностью 6n, где п – число узлов конечного элемента, например п = 3:
|
|
|
i |
|
|
e |
|
|
|
(5.4.3) |
|
|
|
j , |
|||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
Fi |
|
|
F |
e |
|
|
(5.4.4) |
|
|
|
Fj . |
|||
|
|
|
F |
|
|
|
|
|
|
k |
|
Минимизация общей потенциальной энергии конечного элемента приводит к системе линейных алгебраических уравнений
|
|
|
|
|
e |
|
|
|
F e |
|
, |
(5.4.5) |
|
|
|
k e |
|
|
|
||||||
где |
ke |
– матрица жесткости конечного элемента размерностью |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6n 6n . Учитывая, что мембранные усилия приводят к деформированию конечного элемента в его плоскости, а поперечные усилия – к изгибу, воспользуемся полученными ранее матрицами жесткости конечных элементов для пластин. Тогда для деформирования в плоскости конечного элемента
ke
p 6 6
ui |
Ui |
|
|
||
v |
V |
|
|
|
|
|
i |
i |
|
|
|
u j |
U j |
, |
(5.4.6) |
||
|
|
|
|
|
|
vj |
Vj |
|
|
||
|
|
|
|
|
|
uk |
Uk |
|
|
||
v |
|
V |
|
|
|
|
k |
k |
|
|
|
201
а для изгиба
ke
b 9 9
wi |
|
Wi |
|||
|
|
xi |
|
M |
xi |
|
|
|
|
||
|
yi |
|
M yi |
||
|
|
|
|
|
|
wj |
|
Wj |
|||
|
xj |
|
|
|
|
|
|
M xj |
|||
|
|
|
|
M |
|
|
|
yj |
|
|
yj |
wk |
|
Wk |
|||
|
|
|
M |
xk |
|
|
|
xk |
|
||
|
|
|
M |
yk |
|
|
|
yk |
|
||
(5.4.7)
.
Учитывая, что изгибные и мембранные компоненты деформаций не влияют друг на друга, и сопоставляя последние соотношения с (5.4.5), получим матрицу жесткости конечного элемента оболочки в виде
|
|
|
k p |
k p |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
11 |
11 |
|
|
|
|
|
|
|
|
|
k p |
k p |
0 |
0 |
0 |
0 |
|
||
|
|
|
|
11 |
11 |
|
|
|
|
|
|
|
|
|
0 0 kb |
kb |
kb |
0 |
|
|
|||
|
|
|
|
|
|
11 |
11 |
11 |
|
... |
|
|
|
|
0 |
0 |
kb |
kb |
kb |
0 |
|
||
|
|
|
|
|
|
11 |
11 |
11 |
|
|
|
|
|
|
|
0 |
0 kb |
kb |
kb |
0 |
|
|
|
|
|
|
|
|
|
11 |
11 |
11 |
|
|
(5.4.8) |
ke |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
. |
||
|
|
|
k p |
k p |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
11 |
11 |
0 |
0 |
0 |
0 |
|
|
|
|
|
k p |
k p |
|
|
|||||
|
|
|
|
11 |
11 |
b |
b |
b |
0 |
|
|
|
|
|
|
0 |
0 |
k11 |
k11 |
k11 |
... |
|
|
|
|
|
0 0 kb |
kb |
kb |
0 |
|
|
|||
|
|
|
|
|
|
11 |
11 |
11 |
|
|
|
|
|
|
0 |
0 k11b |
k11b |
k11b |
0 |
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||||
Мы рассмотрели получение матрицы жесткости в локальной системе координат, связанной с конечным элементом. Однако при переходе к конструкции в целом необходимо установить связь между локальной и глобальной или конструктивной системами координат, так как:
202

1)координаты узлов при разбиении конструкции задаются
вглобальной системе координат, и для построения матрицы жесткости конечного элемента необходимо их представить в локальной системе координат;
2)построение матрицы жесткости конструкции в целом проводится в глобальной системе координат, следовательно, необходимо преобразовать матрицы жесткости всех конечных элементов оболочки к этой глобальной системе координат;
3)внешняя нагрузка часто задается в локальной системе, например распределенное давление, и при формировании вектора узловых обобщенных нагрузок также необходимо соответствующее преобразование.
Пусть X ,Y , Z – локальная система координат, X, Y, Z – гло-
бальная. Рассмотримобобщенныесилы иперемещенияузлаi. Вектор обобщенных перемещений узла i состоит из двух векторов:
ui ui ,vi , wi вектор перемещений и i xi , yi , zi – вектор углов
поворота. В соответствии с правилами преобразования компонент вектораприпереходекновойсистемекоординатможнозаписатькак
u |
|
x x |
||
|
i |
|
|
|
vi |
y x |
|||
|
|
|
z x |
|
wi |
|
|||
x y
y y
z y
|
u |
u |
|
|
x z vi |
vi |
, |
(5.4.9) |
|
|
y z i |
i |
|
|
|
w |
w |
|
|
|
z z i |
i |
|
|
где |
– матрица направляющих косинусов, например x x – ко- |
|||||||
синус угла между осями |
X и X; аналогично для компонент век- |
|||||||
тора углов поворота |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
xi |
xi |
|
|
||
|
|
|
|
|
|
|
, |
(5.4.10) |
|
|
|
yi |
yi |
||||
|
|
|
|
|
|
|
|
|
|
|
|
zi |
zi |
|
|
||
следовательно, преобразование обобщенных перемещений узла i определим соотношением вида
i |
|
0 |
i L i , |
(5.4.11) |
|
|
|||
|
0 |
|
|
|
203
а для элемента e в целом, содержащего узлы i, j, k,
e |
L |
0 |
0 |
|
|
|
|
|
|
|
L |
|
|
e |
e |
(5.4.12) |
|
|
0 |
0 |
|
T . |
||||
|
|
0 |
0 |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведем аналогичные рассуждения для вектора узловых нагрузок
e |
T F |
e |
|
(5.4.13) |
F |
|
и подставим полученные выражения в формулу (5.4.5), в результате
T T ke T e Fe |
(5.4.14) |
или |
|
ke e F e , |
(5.4.15) |
где матрица жесткости конечного элемента в глобальной системе координат
ke T T ke T . |
(5.4.16) |
Далее задачу решаем обычным образом:
1)формируем глобальную матрицу жесткости;
2)определяем перемещения узлов в глобальной системе координат;
3)для каждого конечного элемента переходим к локальной системе и определяем соответствующие перемещения;
4)находим мембранные и изгибные деформации и ;
5)определяем деформации слоев s z , где z –
расстояние от слоя до срединной поверхности оболочки; 6) используем закон Гука для каждого слоя и определяем
напряжения, и далее по критерию прочности проводим оценку разрушился или нет данный слой в рассматриваемом конечном элементе.
204
Если принадлежащие к узлу i элементы находятся в плоскости, параллельной X, Y (рис. 5.20), то для всех этих элементов будут выполняться равенства: z z 1, z x z y 0, и в этом случае
строка и столбец глобальной матрицы жесткости, соответствующие перемещению zi , будут заполнены нулями. Вместо этого
уравнения имеем тождество 0 0 .
Можно исключить это уравнение из системы линейных алгебраических уравнений, но это, как правило, усложняет алгоритм: поиск узлов, все элементы при которых находятся в плоскости, параллельной XY, и исключение соответствующих уравнений. Обычно модифицируют матрицу жесткости элемента:
|
|
|
|
|
|
ke |
|
|
|
|
|
|
|
|
k p |
k p |
|
|
k p |
k p |
|
|
|
|
|
||||
|
p |
k |
p |
|
|
k |
p |
k |
p |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
kb |
kb |
kb |
|
|
|
kb |
kb |
kb |
|
|
|
|
|
|
kb |
kb |
kb |
|
|
|
kb |
kb |
kb |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
kb |
kb |
kb |
|
|
|
kb |
kb |
kb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.4.17) |
|
|
k p |
|
|
k p |
k p |
|
|
|
|
, |
|||
k p |
|
|
|
|
|
|
||||||||
k p |
k p |
|
|
k p |
k p |
|
|
|
... |
|
||||
|
|
|
|
kb |
kb |
kb |
|
|
|
kb |
kb |
kb |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
kb |
kb |
kb |
|
|
|
kb |
kb |
kb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kb |
kb |
kb |
|
|
|
kb |
kb |
kb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где α некоторое «малое» число; малое в смысле 0 , но обеспечивающее хорошую обусловленность системы уравнений. Наличие произвола в выборе, а в локальной матрице жесткости элемента повлияет на обобщенное перемещение zi , но так как эта
величина не входит в определение мембранных и изгибных де-
205

формаций, поэтому ее значение не повлияет и на напряжения, возникающие в конструкции.
Рис. 5.20. Пример расположения конечных элементов
Локальные направляющие косинусы
A. Прямоугольные элементы для цилиндрических или коробчатых тонкостенных конструкций (рис. 5.21)
Рис. 5.21. Дискретизация цилиндрической поверхности
x x 1, |
|
x y 0, |
(5.4.18) |
x z 0; |
|
206
|
|
y x 0, |
|
|||||||
|
y y |
Yj Yi |
, |
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
d |
|
|||
|
y |
z |
Z j Zi |
; |
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
d |
|
|||
|
|
z x 0, |
|
|||||||
|
z y |
Z j Zi |
, |
|||||||
|
d |
|||||||||
|
|
|
|
|
|
|
||||
|
z z |
Yj Yi |
, |
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
d |
|
|||
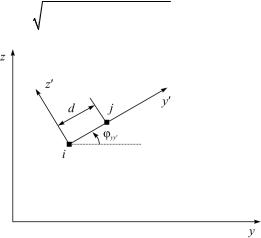
где величина d |
Z j Zi 2 |
Yj Yi 2 |
(рис. 5.22). |
|||||||
(5.4.19)
(5.4.20)
Рис. 5.22. Ориентация стороны конечного элемента
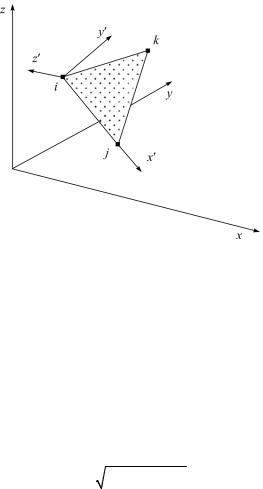
Б. Треугольные элементы. Пусть X ,Y , Z и X ,Y , Z координатные оси соответственно глобальной и локальной ортого-
нальных систем координат, ось X |
направлена вдоль стороны |
конечного элемента (ij), ось Y |
ортогональна X и лежит |
в плоскости конечного элемента (рис. 5.23). Сторона (ij) определяется вектором
207
X j
Vij Yj
Z j
Xi |
|
X ji |
|
|
|
Yi |
|
|
|
, |
(5.4.21) |
|
Yji |
|
|||
Zi |
|
|
|
|
|
|
Z ji |
|
|
|
Рис. 5.23. Локальная и глобальная системы координат конечного элемента
и искомые направляющие косинусы можно получить делением компонент этого вектора на его длину:
x x |
|
1 |
X ji |
||
|
|
|
|
||
Vz x y |
|
|
Yji |
||
l |
|||||
|
|
|
|
||
|
ij |
||||
x z |
|
|
Z ji |
||
где длина вектора Vij
lij X 2ji Yji2 Z 2ji
,
.
(5.4.22)
(5.4.23)
Построим ось Z как нормаль к плоскости треугольника i, j, k. Для этого воспользуемся векторным произведением
208
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
k |
||||
|
|
Vz Vij Vik |
det |
X ji |
|
|
|
Yji |
|
Z ji |
|
||||||||||||
|
|
|
|
|
|
|
|
|
Xki |
|
|
|
Yki |
|
Zki |
|
|||||||
|
|
Yji Zki Yki Z ji |
|
Z ji Xki |
Zki X ji |
|
X jiYki XkiYji |
||||||||||||||||
i |
j |
k |
|||||||||||||||||||||
|
|
|
|
Y |
ji |
Z |
ki |
Y Z |
ji |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ki |
|
|
|
|
|
|
|
|
|
||||||
|
|
Z ji Xki |
Zki X ji |
; |
(5.4.24) |
||||||||||||||||||
|
|
|
|
X |
|
Y |
X |
ki |
Y |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ji |
ki |
|
|
|
|
|
ji |
|
|
|
|
|
|
|||||
для определения направляющих косинусов разделим вектор Vz на его длину:
z x |
|
1 |
|
Yji Zki |
||||
|
|
|
|
|
|
|
||
vz z y |
|
|
Z ji Xki |
|||||
lz |
||||||||
|
|
|
|
X |
ji |
Y |
||
|
z z |
|
|
|
|
ki |
||
Yki Z ji
Zki X ji
XkiYji
. (5.4.25)
Направляющие косинусы оси Y |
можно получить как век- |
|||||
торное произведение векторов vx и vz , таким образом: |
|
|||||
y x |
|
|
z y x z z z x y |
|
||
|
|
vz vx |
|
... |
|
(5.4.26) |
vy y y |
|
|
|
|||
|
|
|
|
... |
|
|
y z |
|
|
|
|
|
|
нормировать вектор vy |
не надо, так как векторы vx и vz |
являют- |
||||
ся единичными.
Расчет тонкостенных элементов конструкций с ребрами жесткости (рис. 5.24). L, R, ho – соответственно длина, радиус и толщина оболочки, h, b, t, a – соответственно высота, ширина ребра, расстояние и угол между ребрами (рис. 5.24, б). Ребро – стержневой конечный элемент, который работает на изгиб, оболочка – плоский конечный элемент, работает на изгиб, растяжение и сжатие. Возможно построение специальных конечных элементов – суперэлементов.
209

Рис. 5.24. Конструкция (а) со спирально-винтовой системой ребер (б)
5.5.Осесимметричные оболочки
1.Геометрия оболочки. Пусть r r(z) – образующая осе-
симметричной оболочки, r, φ, z конструктивная или глобальная система координат, w, u компоненты вектора перемещений точки срединной поверхности в локальной системе координат: w – по
нормали к |
образующей, и – смещение |
вдоль образующей |
|
(рис. 5.25). |
Введем локальную систему |
координат |
s, , : |
s – вдоль образующей, – по кольцевому направлению, |
– по |
||
нормали к поверхности оболочки.
Рис. 5.25. Осесимметричная оболочка
210
