Тема :случайная величина и ее числовые характеристики числовые характеристики дискретных случайных величин

Задание № 1. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины, заданной законом распределения:

Х	4	6	7	8
Р	0,25	0,5	0,1	0,15

Вначале полено проверить условие = 1. (1)

0,25 + 0,5 + 0,1 + 0,15 = 1, то условие (1) выполняется.

Дисперсия случайной величины вычисляется по формуле: D(Х) = М(Х) - (М(Х)), где

М(Х) – математическое ожидание:

М(Х) = .

В нашем случае

М(Х) =

(М(Х))= (5,9)= 34,81

При нахождении М(Х) считается, что квадраты значений величины Х

принимаются с теми же вероятностями, что и значения Х, т.е. закон распределения случайной вероятности Хтаков:

Х	16	36	49	64
Р	0,25	0,5	0,1	0,15

М(Х) =

D(Х) = 36,5 – 34,81 = 1,69

Среднее квадратичное отклонение находится по формуле

Ответ: D(X) = 1.69;

Задание №2.Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

Х	60	20	40	50
Р	0,5		0,35	0,1

Закон распределения в данном виде полностью дискретную случайную величину Х не описывает, т.к. неизвестна вероятность Р₂ значения х₂ = 20.

Но учитывая условие , можно доопределить данный закон, найдя р₂ по формуле:

р₂ = 1-(р₁+р₃+р₄) = 1-(0,5+0,35+0,1) = 0,05

Найдем математическое ожидание М(Х):

.

Тогда (М(Х))²≈1400

Закон распределения случайной величины Х² таков:

Х2	3600	400	1600	2500
Р	0,5	0,05	0,35	0,1

Дисперсия находится по известной формуле:

D(X) = M(X²) – (M(X))² = 2630 – 1400 = 1230, а

среднее квадратическое отклонение:

Ответ: D(X) = 1230, 35.

Числовые характеристики непрерывных случайных величин

Задание 1. Найти дисперсию и среднее квадратичное отклонение, если задана непрерывная случайная величина интегральной функцией распределения:

Найдем дифференциальную функцию распределения:

Математическое ожидание X и X²:

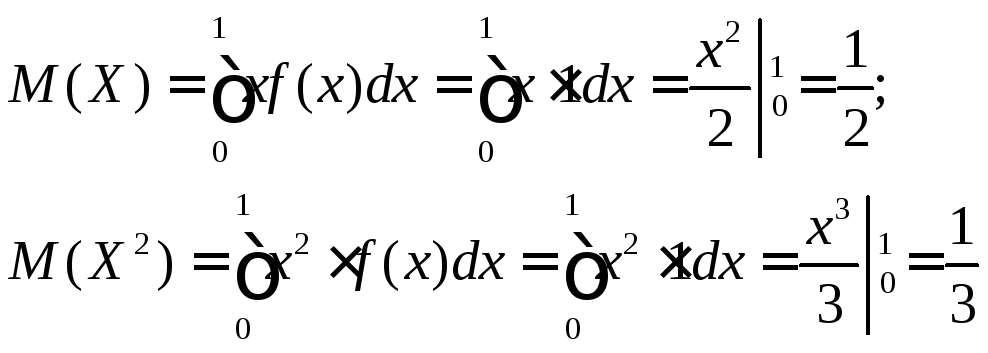
Тогда:

Ответ: D(X) =,

Задание 2. Случайная величина X распределена но нор­мальному закону. Математическое ожидание и среднее квад­ратическое отклонение этой случайной величины соответствен­но равны 2 и 5. Найти вероятность того, что случайная вели­чина в результате испытания примет значение, принадлежа­щее интервалу (1;5).

Решение. Вероятность того, что случайная величина X, имеющая нормальное распределение, примет одно из своих возможных значений в интервале (α;β), вычисляется по фор­муле

P(α< x<β)= Ф- Ф

Здесь a=М(х), σ = , Ф (x) = dt

функция Лапласа.

По условию задачи α=1, β=5, a=2, σ=5. Следователь­но,

Р(1<Х<5)=Ф — Ф=Ф(0,6) —Ф(—0,2).

Так как функция Лапласа нечетна, то

Ф(—0,2)=—Ф(0,2).

Таким образом,

P(1<Х<5)=Ф(0,6)+ Ф(0,2).

По табл. 2 приложения находим

Ф (0,6) =0,2257, Ф (0,2) =0,0793.

Искомая вероятность равна

Р(1<Х<5)=0,2257+0,0793=0,305.

Ответ: 0,305

Задание3.Непрерывная случайная величина имеет нормальное распределение. Ее ,. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (30;36).

Решение: Воспользуемся формулой

, где

Ответ: 0,1586

Задание 2. Случайные значения веса зерна распределе­ны нормально. Математическое ожидание веса зерна равно 0,15 г, среднее квадратическое отклонение равно 0,03. Найти вероятность того, что вес наугад взятого зерна отклонится от математического ожидания не более, чем на 0,06г.

Решение. Вероятность того, что отклонение случайной величины X, имеющей нормальное распределение, от ее ма­тематического ожидания a по абсолютной величине, не будет превосходить заданного положительного числа ɛ, определяет­ся по формуле

Р(│Х—a│≤)=2Ф

По условию задачи a =0,15; σ = 0,03;  =0,06.

Следовательно,

P (│x-0,15│≤0,06) = 2Ф= 2Ф(2).

По табл. 2 приложения находим Ф(2)=0,4772. Искомая вероятность равна

Р(│Х—0,15│ ≤0,06) = 2 · 0,4772=0,9544.

Ответ: 0,9544