
- •Министерство образования и науки российской федерации
- •Часть 1. Гамма-, бета- и пси-функции
- •390005, Рязань, ул. Гагарина, 59/1.
- •Предисловие
- •§ 1. Гамма-функция Эйлера (Эйлеров интеграл 2 рода)
- •Определение и простейшие свойства гамма-функции в комплексной области
- •Рассмотрим замкнутую область(см. Рис. 1.1).
- •Дальнейшие свойства гамма-функции
- •Примеры
- •Примеры на применение формулы
- •Другое интегральное представление гамма-функции и следствия из него
- •§ 2. Бета-функция Эйлера (Эйлеров интеграл 1 рода)
- •2.1. Определение и связь с гамма-функцией
- •2.2. Свойства бета–функции
- •2.3. Некоторые обозначения и символы
- •§ 3. Гамма-функция в вещественной области
- •Функциональная характеристика гамма-функции
- •3.2. График функции
- •3.3. График функции
- •4.2. Функция прии ее график
- •4.3. Дальнейшие свойства пси-функции
- •4.4. Вычисление преобразования Лапласа некоторых элементарных функций
- •4.4.1. Преобразование Лапласа функции
- •4.4.2. Преобразование Лапласа функции
Примеры
Приведем далее несколько примеров на применение полученных формул при вычислении интегралов.
Пример 1.1

![]()
![]() ,
,
причем последний
интеграл, а с ним и исходный, сходятся
при
![]()
Пример 1.2.

 .
.
Пример 1.3.
![]() .
.
Пример 1.4.
![]() =
=




Примеры на применение формулы

Пример 1.5.
![]()
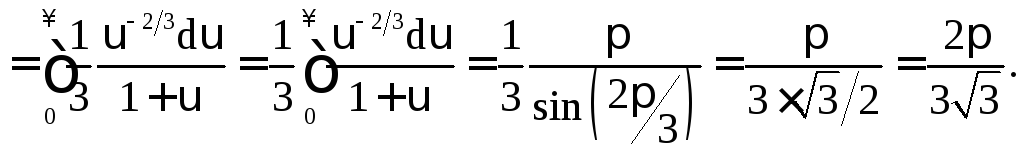
Пример 1.6.
 .
.
Пример 1.7.

![]() .
.
Пример 1.8
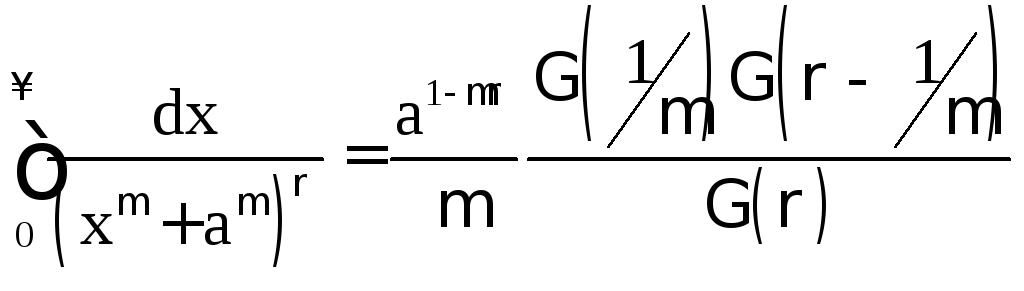
![]() .
.
Пример 1.9.

![]()
Интеграл сходится,
если

Пример 1.10.
![]() .
.
Решение. Рассмотрим интеграл
![]() .
.
Вычислим




причем интеграл
![]() сходится тогда и только тогда, когда
сходится тогда и только тогда, когда
![]()
Таким образом, при
![]()

![]()
Пример 1.11.
![]() ,
причем величина
,
причем величина![]() найдена в предыдущем примере. Следовательно,
найдена в предыдущем примере. Следовательно,


![]()
 .
.
Пример 1.12.
 .
.


причем все интегралы
сходятся
![]()
![]()
![]()
![]() .
.
Таким образом, при
![]()
 ;
;

![]() .
.
Пример 1.13.
 .
.
Решение.
![]()
![]() .
Отсюда
.
Отсюда
![]()
Но
![]() ,
т.е. при
,
т.е. при![]()
 .
.
При
![]() отсюда получается любопытный интеграл
отсюда получается любопытный интеграл

![]() .
.
Пример 1.14.

где
 (см. пример 1.9). Отсюда
(см. пример 1.9). Отсюда
![]()
![]()
Пример 1.15.
Докажем, что при
![]()
![]()
При
 сделаем замену переменной
сделаем замену переменной
![]() ;
;
![]()
![]()
причем интеграл
сходится
![]() .
.
При
 проходит та же замена переменной
проходит та же замена переменной ,
,
но теперь пределы интегрирования меняются местами:
![]()
![]()
причем для сходимости
интегралов по-прежнему должно выполняться
условие
![]() .
.
Пример 1.16.
 .
.
Обозначим
![]()
 ,
,
причем для сходимости
интегралов должно выполняться условие
![]() .
.
При этих значениях
a


Пример 1.17.
Рассмотрим интеграл
![]() .
Этот интеграл сходится, так как в
окрестности нуля
.
Этот интеграл сходится, так как в
окрестности нуля![]() а интеграл
а интеграл![]() сходится.
сходится.
Сделаем в
![]() замену переменной
замену переменной![]()
![]()
![]()
![]()
![]()

Таким образом,
![]()
Пример 1.18. Раабе рассмотрел интеграл
![]()
Так как
![]()
![]() то
то
![]()
Так как
![]() сохраняет непрерывность при
сохраняет непрерывность при![]() то
то
![]() .
.
С другой стороны,
![]()
![]()
![]() и
и
![]() .
.
Пример 1.19. Рассмотрим интеграл
![]()
Сделаем в нем
замену переменной
![]()
![]()
![]()
![]()

![]()



 .
.
Последний интеграл вычислим «по частям»:
 .
.
Тем самым
![]() .
.
Другое интегральное представление гамма-функции и следствия из него
1.4.1.
Докажем, что при
![]() имеет место формула
имеет место формула
![]() (1.7)
(1.7)
Д оказательство.
оказательство.
Рассмотрим
замкнутый контур
![]() ,
изображенный на рис. 1.7. Так как при
фиксированном
,
изображенный на рис. 1.7. Так как при
фиксированном![]() функция
функция![]() - аналитическая, то согласно теореме
Коши
- аналитическая, то согласно теореме
Коши![]() .
.
С другой стороны,
![]()
(1.8)
![]() .
.
Оценим подынтегральную функцию в (8) по модулю:
![]() .
.
Пусть
![]()
![]() фиксировано. Тогда при
фиксировано. Тогда при![]()
![]() ,
если
,
если
![]() .
Следовательно, согласно лемме Жордана
.
Следовательно, согласно лемме Жордана![]() при
при![]() .
.
Далее,
 при
при![]() ,
,
если
![]() .
Остается рассмотреть интеграл
.
Остается рассмотреть интеграл![]() .
Сделаем в нем замену переменной
.
Сделаем в нем замену переменной![]() ,
,![]() .
Получим:
.
Получим:
![]()
![]()
![]()
 .
.
Устремляя
в (8)
![]() и
и![]() ,
получаем при
,
получаем при
![]()
![]() ,
ч.т.д.
,
ч.т.д.
1.4.2.
Докажем что при
![]()
![]()
![]() ,
(1.9)
,
(1.9)
![]()
![]() . (1.10)
. (1.10)
Доказательство.
Взяв в формуле
(7)
![]() и отделяя вещественную и мнимую части,
получаем:
и отделяя вещественную и мнимую части,
получаем:
![]() Формулы
(9) и (10) вытекают отсюда с помощью
аналитического продолжения.
Формулы
(9) и (10) вытекают отсюда с помощью
аналитического продолжения.
Интегралы более общего вида

![]() (1.11)
(1.11)
и

![]() (1.12)
(1.12)
вытекают
из (3) и (4) соответственно при
![]() с помощью замены переменной
с помощью замены переменной![]() и аналитического продолжения.
и аналитического продолжения.
1.4.3. Докажем, что
![]() (1.13)
(1.13)
и
![]() (1.14)
(1.14)
Решение. Имеем:
![]() .
.
Далее
выполним в формуле (7)
![]() замену переменной
замену переменной
![]() ;
;
![]()
![]()
![]() .
.
В
частности, при
![]()
![]() ,
,
откуда, отделяя вещественную и мнимую части, получаем интегралы (13) и (14).
1.4.4.
Докажем, что при
![]()

Решение.
Первым делом выполним в интеграле
![]() замену
переменной
замену
переменной .
.
Получим:
 .
.
Этот
интеграл сходится в нуле при
![]() ;
;
сходится
на бесконечности при
![]() .
.
Тем
самым при
![]()
 .
.
Далее
воспользуемся формулой (7)
![]() .
.
Взяв
здесь
![]() ,
при
,
при![]() получаем
получаем


![]() .
.
При
![]()
 .
.
