
Metod_pos_prakt
.pdf
где
S |
|
|
s |
2 |
|
2 |
min |
|
|
||||
|
|
|
|
|
|
– расстояние от начала координат до ближайшей осо-
бой точки (нуля или полюса, см. рис. 6.5).
Это расстояние определяется как модуль особой точки, началу координат: S = p0 или S = p* .
За верхнюю граничную частоту fВ можно взять значение
|
|
|
(2 4)S |
max |
|
f |
|
|
|
, |
|
В |
2 |
|
|||
|
|
|
|
ближайшей к
(6.21)
где Smax – расстояние от начала координат до самой удаленной особой точки (см. рис. 6.5).
В процессе предварительного расчета характеристик значения fН и fВ можно корректировать в любую сторону.
Пример 6.5. Оценить граничные частоты частотной характеристики коэффициента передачи в примере 6.3.
Решение. Передаточная функция (6.10) имеет один нуль p01 = 104 и два комплексно-сопряженных полюса p*1,2 = (-5.5 j8.35)106. Следовательно,
Smin = p0 =104, |
|
|
Smax = p* = 107. |
||||||
Таким образом, нижнюю граничную частоту (6.20) можно принять близ- |
|||||||||
кую, например, к |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
4 |
|
|
|
|
|
f |
|
|
|
5000 Гц. |
|
||
|
|
Н |
2 |
3 |
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|||||||
Верхняя граничная частота может быть оценена по формуле (6.21) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 S |
max |
|
|
|
|
|
f |
|
|
|
8 МГц. |
|
||
|
|
В |
2 |
|
|
||||
|
|
|
|
|
|
|
|||
При вычислениях частотных характеристик используют циклическую частоту f [Гц], а фазовый угол измеряют в градусах φ [град], как это принято в технике. Число значений частот следует брать 10 – 20 на график с неравномерным шагом. Вблизи экстремумов функции шаг изменения частоты уменьшают. В точках экстремумов, т.е. при частотах, соответствующих особым точкам Si,
f = (Si, S2,…Sj)/(2 ) обязательно вычисляют модуль и аргумент функции.
Пример 6.6. Провести численный расчет АЧХ, ФЧХ, АФХ коэффициента передачи по напряжению фильтра по аналитическим выражениям (6.17), (6.18) и (6.19), полученным в примере 6.4.
Решение. Расчет можно провести по готовым вычислительным программам, например, «Mathcad», «Пакет вычислительных программ для курсовой работы по ОТЦ (кафедра ТРЭ)» и др. Сначала проводится предварительный расчет по выбранным значениям fН = 5 кГц и fВ = 8 МГц. По результатам расчета
41
уточняют значения граничных частот, которые могут определяться диапазоном изменения коэффициента передачи. В данном примере целесообразно выбрать fН = 100 кГц и fВ = 30 МГц.
Перед построением частотных характеристик нужно выбрать тип масштаба по осям графика – линейный, полулогарифмический или логарифмический. Для этого целесообразно придерживаться принятым в технике рекомендациям.
Если диапазоны изменения частоты по оси абсцисс и функции (коэффициент передачи) по оси ординат составляют два и более порядков, то пользуются логарифмическим масштабом по двум осям. Если диапазон изменения одной величины (частоты или функции) не больше двух порядков, то пользуются полулогарифмическим масштабом (по одной оси линейный масштаб). Если диапазоны частоты и функции не превышают двух порядков, то график изображают в линейном масштабе.
K(f) |
100 |
0 φ |
|
B(f) |
|
|
|
|
|
|
0 |
|
f,Гц |
A(f) |
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
f, Гц |
|
|
|
|
-1000 |
|
|
|
а) |
|
б) |
|
в) |
Рис.6.7
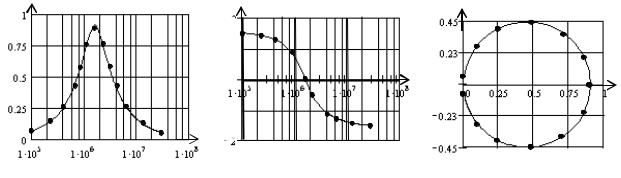
В нашем примере частоты fН и fВ отличаются в 300 раз, т.е. более двух порядков. Коэффициент передачи KU(f) изменяется примерно в десять раз (от 0.1 до 1.0). Поэтому частотные характеристики целесообразно строить в полулогарифмическом масштабе.
На рис.6.7 а), б), в) изображены АЧХ, ФЧХ, АФХ соответственно, рассчитанные по программе «Mathcad» и построенные по точкам.
42

ТЕМА 7. РАСЧЕТ ПЕРЕХОДНЫХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ЦЕПЕЙ ОПЕРАТОРНЫМ МЕТОДОМ
7.1. Переходные процессы в электрических цепях. Законы коммутации
Режим работы цепи, при котором токи и напряжения ветвей являются периодическими функциями времени или сохраняют неизменные значения, называется установившимся. Если токи и напряжения изменяются не по периодическому закону, то режим работы цепи называется неустановившимся.
Частным случаем этого режима являются переходные процессы, которые возникают при переходе от одного установившегося режима к другому. Причинами переходных процессов могут быть включение сигнала в цепь, изменение параметров сигнала или цепи и т.д. Переходной процесс в цепи обусловлен наличием в ней реактивных элементов (индуктивности, емкости), в которых накапливается энергия магнитного и электрического полей. При изменении установившегося режима изменяется энергетический режим работы цепи. Эти изменения не могут осуществляться мгновенно в силу непрерывности изменения энергии магнитного и электрического полей, что и приводит к возникновению переходных процессов.
В основе методов расчета переходных процессов лежат законы коммутации. Коммутацией принято считать любое изменение установившегося режима или состояния цепи. Принято считать, что коммутация совершается мгновенно. Если считать, что коммутация осуществляется в момент t = 0, то момент времени до коммутации обозначают t = 0 , момент непосредственно после коммутации – t = 0+. Различают два закона коммутации.
Первый закон коммутации связан с непрерывностью изменения магнитного поля индуктивности WL = L iL 2/2 и гласит:
в начальный момент t = 0+ ток в индуктивности имеет тоже значение, что и в момент t = 0 до коммутации, а затем плавно
изменяется
iL(0+) = iL(0 ).
В отличие от тока iL напряжение на индуктивности uL(t) может изменяться скачком.
Второй закон коммутации связан с непрерывностью изменения электрического поля емкости WC = C uC 2/2 и гласит:
43

в начальный момент t = 0+ напряжение в емкости имеет тоже значение, что и в момент t = 0 до коммутации, а затем плавно
изменяется
uC(0+) = uC(0 ).
В отличие от напряжения uC ток через емкости iC(t) может изменяться скачком.
Значения токов iL(0+) и напряжений uC(0+) в момент коммутации образуют начальные условия задачи по расчету переходных процессов. Если эти величины равны нулю iL(0 ) = 0, uC(0 ) = 0, то такие начальные условия называются нулевыми. Если iL(0 ) 0, uC(0 ) 0, то эти начальные условия называются ненулевыми. Начальные условия являются независимыми величинами.
7.2. Переходные характеристики линейных цепей
Переходной характеристикой h(t) цепи называют отклик y(t) цепи на воздействие x(t) в форме единичной ступенчатой функции x(t) = 1(t).
|
|
|
x |
|
1, при t 0, |
|
|
1 |
|
|
x(t) 1(t) |
(7.1) |
|||
|
|
||||||
|
|
|
|
||||
|
|
|
|
0, при t 0. |
|
||
|
|
|
|
|
|||
|
|
|
|
|
t |
Единичная ступенчатая функция изображена на рис. |
|
|
|
|
Рис.7.1 |
7.1. Если ступенчатая функция имеет амплитуду X0, не |
|||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
равную единице, то переходная характеристика определя- |
|
ется так: h(t) = y(t)/X0. Переходная характеристика h(t) и отклик x(t) обязательно обладают соответствующей размерностью.
Переходная характеристика тока или напряжения характеризует переходной процесс в цепи при нулевых начальных условиях, вызванный включением в момент t = 0 воздействия (напряжения или тока) в виде скачка (7.1).
Расчет переходных процессов сводится к задаче определения отклика y(t) при включении заданного воздействия x(t), при изменении параметров воздействия или параметров цепи при заданных начальных условий. Эти задачи могут быть решены классическим методом путем решения дифференциальных уравнений относительно независимой переменной iL или uC . Однако, значительно проще эти задачи решаются операторным методом.
7.3. Операторный метод анализа переходных процессов
В основе операторного метода лежит преобразование Лапласа, которое позволяет перенести решение из области функции f(t) действительного переменного t в область функции F(p) комплексного переменного p = α + j . Функ-
44

ция f(t) называется оригиналом, а F(p) – изображением. Сокращенная запись преобразования имеет символику, например,
f(t) F(p); |
f(t) F(p). |
Изображение F(p) может быть вычислено по прямому преобразованию Лапласа
|
|
|
pt |
|
|
F(p) |
|
f(t)e |
dt. |
||
|
|||||
|
0 |
|
|
|
Обратное преобразование Лапласа позволяет вычислить оригинал f(t) по известному изображению F(p)
|
1 |
c j |
|
|
|
f(t) |
F(p)e |
pt |
dp. |
||
|
|||||
|
|
||||
|
2πj |
|
|
||
|
|
c j |
|
|
|
Операторные передаточные функции
Операторной передаточной функцией T(p) называется отношение изображения отклика y(p) к изображению входного воздействия x(p) при нулевых начальных условиях
Т(p) |
y(p) |
. |
|
x(p) |
|||
|
|
||
|
|
|
(7.2)
Передаточные функции имеют разные названия и разный физический смысл в зависимости от вида воздействия и отклика.
Например, если y(p) = U2(p) – выходное напряжение, x(p) = U1(p) – входное напряжение, тогда передаточная функция T(p) является операторным ко-
эффициентом передачи по напряжению и обозначается так
Другой пример:
|
T (p) |
|||
|
|
U |
|
|
T |
(p) Z(p) |
U |
2 |
(p) |
|
|
|||
|
|
|
||
Z |
|
I |
(p) |
|
|
|
|||
|
|
1 |
|
|
|
|
U |
(p) |
|
|
KU |
(p) |
2 |
|
. |
|
U (p) |
|||||
|
|
|
|||
|
|
1 |
|
|
|
передаточное сопротивление и т.д.
Операторную передаточную функцию можно определить, не прибегая к прямому преобразованию Лапласа. Для этого в соответствующей комплексной передаточной функции T(j ) нужно заменить мнимую частоту j на комплексную переменную p = α + j :
T(j ) j =p = T(p).
Операторная передаточная функция позволяет определить операторное изображение отклика, если известно изображение произвольного воздействия x(p):
45
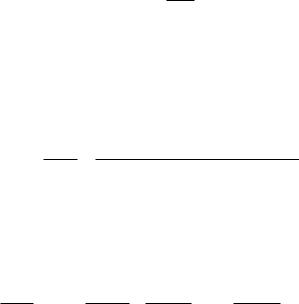
y(p) = T(p) x(p). |
(7.3) |
|
|
Например, если известен коэффициент передачи по напряжению KU(p) и входное напряжение U1(p), то можно определить операторное выходное напря-
жение U2(p): U2(p) = KU(p) U1(p).
С помощью операторной передаточной функции можно получить операторное выражение переходной характеристики h(p) = y(p) – операторный отклик. Для этого нужно взять в качестве воздействия x(p) операторное изображение единичного скачка, равное
1(t) 1(p) = 1/p. |
(7.4) |
Таким образом, операторное изображение переходной характеристики определяется формулой
h(p) T(p) 1(p) |
T(p) |
. |
|
p |
|||
|
|
||
|
|
|
(7.5)
7.4. Вычисление оригинала по заданному операторному изображению
Операторное изображение функции y(p) линейной цепи имеет, как правило, вид рациональной дроби
|
M(p) |
|
a |
m |
p |
m |
a |
|
|
p |
m-1 |
...a p a |
|
|
|||
|
|
|
m-1 |
|
|
0 |
|
||||||||||
y(p) |
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
||||
N(p) |
|
|
|
p n b |
|
p n-1 |
|
|
|
|
|||||||
|
|
b |
|
|
...b p b |
|
|
||||||||||
|
|
|
|
n |
|
|
n-1 |
|
|
|
|
1 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.6)
где am, am-1,…a0; bn, bn-1,…b0 – вещественные коэффициенты.
Оригинал y(t) можно вычислить с помощью обратного преобразования Лапласа. Для этого нужно разложить y(p) на простые дроби
M(p) |
|
|
|
A |
|
A |
|
|
A |
|
y |
|
|
1 |
|
2 |
|
... |
n |
, |
|
|
|
|
||||||||
|
0 |
|
|
|
|
|||||
N(p) |
|
p p |
|
p p |
|
|
p p |
|
||
|
|
|
2 |
|
||||||
|
|
|
|
1 |
|
|
|
|
n |
|
(7.7)
где y0=am/bn – масштабный коэффициент, A1, A2 …An – коэффициенты
простых дробей, |
p1, |
p2, |
…pn – корни уравнения знаменателя |
||||
N(p) pn |
bn 1 |
pn 1 ... |
b1 |
p |
b0 |
0 , их называют полюсы функции y(p). |
|
|
|
|
|||||
|
bn |
|
bn |
|
bn |
|
|
Для нахождения оригинала простых дробей с целью упрощения решения задачи целесообразно воспользоваться таблицами оригиналов и изображений известных функций, приведенных в специальных справочниках. В табл. 7.1 даны оригиналы и изображения некоторых функций, встречающихся в теории цепей.
46

|
|
|
|
|
|
Таблица .7.1. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
№ п/п |
Изображение y(p) |
Оригинал y(t) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
A/p |
A = const |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
A |
δ(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1/p2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полюсы изображения y(p)).pk = k действительное число |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
1/(p + ) |
e t |
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
p/(p + a) |
– a·e–a·t |
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
1/[p(p + )] |
(1 e t)/ |
|
|
|
|
|
|
|
|
|
|
||||
7 |
1/[p2·(p + a)] |
(e–a·t + a·t – 1)/ a2 |
|
|
|
|
|
|||||||||
8 |
1/(p + )2 |
t e t |
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
p/(p + )2 |
(1 t)e t |
|
|
|
|
|
|
|
|
|
|
||||
10 |
1/[p(p + )2] |
[1 e t (1 + t)]/ 2 |
|
|
|
|
|
|||||||||
11 |
1/[(p + 1)(p + 2)] |
(e t e t)/( 2 1) |
|
|
|
|
|
|||||||||
12 |
1/[p(p + 1)(p + 2)] |
|
1 |
|
|
1 |
|
|
e |
α1 t |
e |
α2 t |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
α α |
α |
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
α |
2 |
|
α |
|
α |
2 |
|||||||
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
||||||||||||
13 |
p/[(p + 1)(p + 2)] |
( 1 e t 2 e t)/( 1 2) |
|
|
||||||||||||
|
pk,k+1 = j комплексно-сопряженные полюсы. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14 |
(p + )/[(p + )2 + 2)] |
e tcos( t) |
|
|
|
|
|
|
|
|
|
|
||||
15 |
/[(p + )2 + 2)] |
e tsin( t) |
|
|
|
|
e t |
|
|
|
|
|
||||
16 |
p/(p + )2 + 2 |
cos t sin t |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
1/p2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
sin t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
18 |
p/p2 + 2 |
cos t |
|
|
|
|
|
|
|
|
|
|
|
|
||
Чтобы воспользоваться этой таблицей, нужно рассчитать коэффициенты Ak простых дробей (7.7). В математике это делают методом сравнения коэффициентов полиномов. Однако в теории цепей для упрощения расчетов при определении коэффициентов дробей и оригинала применяют теорему разложения.
Теорема разложения
Если изображение y(p) представлено в виде рациональной дроби вида (7.6), то оригинал y(t) можно определить по формулам теоремы разложения. В зависимости от вида полюсов изображения y(p) существует несколько формул разложения, которые приводятся ниже.
47

1. Случай простых, не кратных полюсов.
Если функция y(p) = M(p)/N(p) имеет n простых полюсов, ных и отрицательных – p1 = 1, p2 = 2,… pn = n, то оригинал ется по формуле:
|
α |
|
t |
|
α |
|
t |
|
α |
|
t |
|
n |
M(p k ) |
|
|
p |
|
t |
|
y(t) A e |
1 |
A e |
2 |
... A e |
n |
|
|
|
e |
k |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dN(p)/dp |
p |
p |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действитель- y(t) определя-
. |
(7.8) |
|
|
2. Среди n полюсов имеется один нулевой полюс, например, p1 = 0, p2 = 2,… pn = n , т.е. N(p) = pN1(p).
Формула (7.8) примет вид
|
M(p) |
|
|
α |
2 |
t |
|
α |
n |
t |
|
M( 0 ) |
|
n |
|
M(p |
k |
) |
|
y(p) |
y(t) A |
A |
e |
|
... A |
e |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
pN (p) |
1 |
2 |
|
|
|
n |
|
|
|
|
N ( 0 ) |
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
p |
|
dN (p)/dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
p p |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
k |
t |
|
e |
. |
||
|
(7.9)
3. Среди n полюсов есть пара комплексно–сопряженных, например, p1,2 = – ± j .
В оригинале двум членам суммы (7.7) с этими полюсами соответствует функция в виде затухающего гармонического колебания:
|
|
|
p t |
|
|
|
|
p |
t |
|
M(p |
) e |
1 |
|
|
M(p |
) e |
|
2 |
|
1 |
|
|
|
|
|
2 |
|
2 Acos(ω t) B sin(ω t) e αt 1(t), |
p |
dN(p)/dp |
p p |
p |
2 |
dN(p)/dp |
p p |
|||
*1 |
|
|
|
|
|||||
|
1 |
|
|
|
|
2 |
|||
(7.10)
где A и B – коэффициенты, определяемые по формуле
A jB |
M(p |
2 |
) |
. |
|
|
|||
|
|
|
||
|
dN(p)/dp |
|
p p |
|
|
|
|
2 |
|
(7.11)
4. Случай кратных полюсов.
Если изображение y(p) наряду с n простыми полюсами p1, p2,... pn имеет, например, еще один полюс кратности m в точке pn+1, т.е.
|
|
|
y(p) |
M(p) |
|
|
|
|
M(p) |
|
|
, |
|
|
(7.12) |
||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|||||||
|
|
|
|
N(p) |
|
N1(p) (p pn 1 ) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
то оригинал следует определять по формуле |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
|
M(p k )e pkt |
|
|
|
|
|
|
|
1 d m 1 |
|
M(p)e pn 1t |
|
(7.13) |
|||||
y(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
d |
N1(p) (p pn 1 ) |
|
p p |
|
|
(s 1)! dp m 1 |
|
|||||||||||
k 1 |
m |
|
|
|
N1(p) |
|
|
|
|||||||||||
|
|
dp |
|
k |
|
|
|
|
|
|
p pn 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
48
7.5. Методика расчета переходных характеристик
Процедуру расчета переходных процессов, в т.ч. и переходных характеристик, можно разбить на четыре этапа:
а) вывод формул операторной передаточной функции цепи T(p) и операторной переходной характеристики отклика h(p);
б) получение численного выражения и значений полюсов операторной функции h(p);
в) вывод аналитического выражения переходной характеристики как функции времени h(t);
г) вычисление, построение и анализ переходной характеристики. Рассмотрим все этапы расчета на конкретных примерах.
Пример 7.1. Получить аналитическое выражение операторной переходной характеристики напряжения на конденсаторе hUc(p) = uC(p) в схеме, изображенной на рис. 7.2. На входе цепи включен источник ЭДС ступенчатого напряжения e(t) = u(t) = 1(t) В.
Этот пример охватывает первый этап расчета |
|
|
|
переходной характеристики – вывод формулы опера- |
|
R1 |
|
торной передаточной функции цепи T(p) и оператор- |
|
L |
R3 |
e(t) |
|
||
|
UC |
||
|
|
|
|
ной переходной характеристики отклика h(p). |
|
R2 |
C |
|
|
||
Решение. В соответствии с формулой (7.5) |
|
|
|
требуется рассчитать передаточную функцию T(p) – |
|
Рис. 7.2. |
|
операторный коэффициент передачи по напряжению на емкости KUC(p). В примере 6.2 по теме 6 для этой схемы было получено выражение этого параметра в операторной форме (см. ф. (6.8))
|
|
|
|
|
G (pL R |
2 |
) |
|
|
|
|
|
||
K |
Uc |
(p) |
|
|
1 |
|
|
|
|
|
|
|
. |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
p |
LC p[L(G |
G |
) R |
|
C] 1 R |
|
(G |
G |
|
) |
|||
|
|
|
|
|
||||||||||
|
|
|
2 |
2 |
3 |
|||||||||
|
|
|
|
1 |
3 |
|
|
|
1 |
|
|
|||
На основании (7.5) операторное изображение переходной характеристики будет иметь вид
|
|
|
|
1 |
|
|
G (pL R |
2 |
) |
|
|
|
|
|
|
||||
h |
(p) K |
Uc |
(p) |
|
|
1 |
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Uc |
|
|
p |
p p |
2 LC p[L(G |
G |
|
) R |
|
|
C] 1 R |
|
(G |
G |
|
) |
|
||
|
|
|
|
3 |
2 |
2 |
3 |
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||||
(7.14)
Полученное выражение можно представить в общем виде
|
|
M(p) |
|
|
|
|
p a |
0 |
|
|
H |
0 |
(p a |
0 |
) |
|
|
||
h |
(p) |
H |
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Uc |
|
pN (p) |
|
0 |
p[p |
2 |
b |
p |
b |
] |
p(p p |
|
)(p |
p |
|
) |
|||
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|||||
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
49
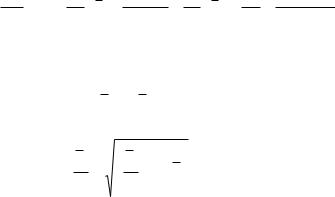
где
|
|
|
|
1 |
|
|
|
R |
|
|
|
(R |
R |
) |
|
R |
|
|
H |
|
|
|
; a |
|
|
2 |
; b |
|
|
1 |
3 |
|
|
2 |
; b |
|
|
0 |
R C |
0 |
L |
|
R R C |
|
L |
|||||||||||
|
|
|
|
1 |
|
|
|
0 |
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
1 3 |
|
|
|
|
|
|
p |
2 |
, p |
3 |
полюсы h |
(p). |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Uc |
|
|
|
|
|
|
|
|
|
||
Получим формулы полюсов путем решения уравнения
1 LC
R (R R |
) |
||
2 |
1 |
3 |
; |
LCR R |
|
||
|
|
||
|
1 3 |
|
|
(7.15)
N(p) p(p |
2 |
b p b |
|
) 0 |
||||||
|
|
|||||||||
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b |
|
2 |
|
|
|
|
|
|
|
|
|
||||
p1=0; |
p |
2,3 |
|
1 |
|
|
1 |
|
|
b . |
|
|
|
|
|
||||||
|
|
|
2 |
|
2 |
|
0 |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
(7.16)
Прежде чем воспользоваться формулами теоремы разложения для нахождения оригинала необходимо получить численное выражение операторной функции hUc(p).
Пример 7.2. Получить численное выражение hUc(p) = uC(p) и значения полюсов функции (7.14) для трех вариантов параметров элементов:
вариант 1) R1 = 10 кОм, R2 = 10 Ом, R3 = 1 кОм, L = 1 мГн, C = 10 пФ;
2)R1 = 10 кОм, R2= 10 Ом, R1= 10 кОм, L= 1 мГн, C = 10 пФ;
3)R1 = 10 кОм, R2 = 10 Ом, R3 = 100 кОм, L = 1 мГн, C = 10 пФ.
Этот пример охватывает второй этап расчета переходной характеристики
–получение численного выражения и значений полюсов операторной функции h(p).
Решение. Подставим значения параметров элементов цепи в формулы коэффициентов (7.15) и полюсов (7.16) операторной функции (7.14). Получим численное выражение переходной характеристики и значения полюсов.
Каждый вариант отличается от другого значением сопротивления резистора R3. Как видно из (7.15) и (7.16) сопротивление R3 влияет на значение полюсов.
Вариант № 1. R1 = 10 кОм, R2 = 10 Ом, R3 = 1 кОм, L = 1 мГн,
C = 10 пФ.
|
|
H 0 107 , a0 104 |
, |
|
|
|
|
|
1.011 1014. |
|
|
||
|
b1 1.001 108 , b0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h (p) 107 |
|
|
p 104 |
|
|
|
|
|
|
|
107 (p 104 ) |
|
. |
|
|
|
|
|
|
|
|
||||||
Uc |
|
p[p |
2 1.001 108 p 1.011 1014 ] |
|
p(p 1.02 106 )(p 9.91 |
107 ) |
|||||||
Полюсы: p1 = 0 – нулевой; p2 = –1.02 106, p3 = –9.91 107 – действительные и отрицательные.
Вариант № 2. R1 = 10 кОм, R2 = 10 Ом, R3 = 9990 Ом, L = 1 мГн, C = 10 пФ.
50
