Metod_pos_prakt

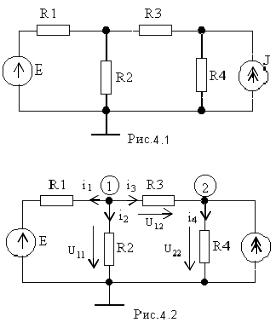
ТЕМА 4. РАСЧЕТ ЛИНЕЙНЫХ ЦЕПЕЙ МЕТОДОМ УЗЛОВЫХ НАПРЯЖЕНИЙ

Метод узловых напряжений основан на применении первого закона Кирхгофа. Он заключается в том, что токи всех ветвей выражаются через так называемые “узловые напряжения”, которые рассматриваются в уравнениях в качестве независимых переменных.

Узловым напряжением k-того узла Ukk называется разность потенциа-

Потенциал базисного узла принимают равным нулю φ0 = 0, поэтому узловое напряжение k-того узла численно равно потенциалу k–того узла: Ukk = φk. Напряжение между двумя узлами можно выразить через узловые напряжения:

Ukn = Ukk – Unn.

Сокращенная система уравнений электрического равновесия цепи, составленная относительно неизвестных узловых напряжений, называется систе-

мой узловых уравнений цепи.

Токи в ветвях определяют по найденным в результате решения уравнений узловым напряжениям по закону Ома: ik = Ukk·g, где g – проводимость ветви, через которую течет ток ik.

Рассмотрим методику формирования узловых уравнений при решении конкретной задачи.

Пример 4.1. Для схемы рис.4.1 составить систему узловых уравнений по первому закону Кирхгофа, в которой за независимые переменные принять узло-

21

U11 и U22. Ток i1 протекает в цепи, в которой включен источник напряжения, ЭДС которого направлена против тока i1. Поэтому i1 = (U11 – E)g1. Направление тока i2 совпадает с направлением U11. Отсюда i2 = U11·g1. Ток i3 протекает между двумя узлами, поэтому i3 = U12·g3 = (U11 – U22)g3. Ток i4 протекает так же как i2 – i4 = U22·g4.

Подставляя выражения токов в уравнения (4.1) и группируя слагаемые при одинаковых напряжениях, получим систему уравнений для определения

Анализируя два уравнения в системе (4.2), нетрудно установить, что они имеют одинаковую структуру. В первом уравнении, составленном для первого узла, узловое напряжение U11 умножается на сумму проводимостей ветвей, подключенных к первому узлу G11 = (g1 + g2 + g3). Во втором уравнении, записанном для второго узла, напряжение U22 также умножается на сумму проводимостей ветвей, подключенных ко второму узлу G22 = g3 + g4.

Если распространить эту закономерность в двух уравнениях на общий случай, то можно ввести новое понятие: собственная проводимость i-го узла Yii. Она равна сумме проводимостей ветвей, подключенных к i-ому узлу. В нашем примере это G11 и G22.

Продолжая структурный анализ уравнений, видим, что в них есть члены, равные произведению узлового напряжения соседнего узла на проводимость ветви, соединяющей два узла: U22∙(–g3) = U22∙G12 – в первом уравнении и U11∙(–g3) = U11∙G21 – во втором уравнении. Проводимости G12 = –g3 и G21 = –g3

называют общими (взаимными) проводимостями i-го и j-го узлов: Yij = Yji. Они равны сумме проводимостей ветвей, включенных непосредственно между этими узлами, взятой с обратным знаком. Если в цепи отсутствуют ветви, включенные между i-м и j-м узлами, то Gij = 0.

В правой части первого уравнения написано значение тока, равное произведению ЭДС E источника напряжения на проводимость ветви g1, включенной последовательно с источником ЭДС, E∙g1. Эта ветвь включена в первый узел. Так как ЭДС направлена от первого узла к базисному, то значение тока берется со знаком плюс.

22

Во втором уравнении в правой части написано значение тока источника, включенного во второй узел, со знаком плюс, так как ток источника втекает в узел.

Таким образом, в правой части уравнений записывается так называемый узловой ток i-го узла Jii. Он равен алгебраической сумме токов источников тока, включенных в данный узел, включая ток, вызванный источником напряжения в ветви, также включенный в i-ый узел. Если токи источников направлены в узел, то они берутся со знаком плюс, если нет – со знаком минус. Если в узловой ток входят токи, вызванные источниками напряжения, то они пишутся со знаком плюс, если ЭДС источника направлена в узел и со знаком минус, если направлена от узла. Узловые токи в примере на рис.4.2 равны J11 = Eg1, J22 = J.

Используя введенные новые понятия для метода узловых напряжений, можно представить систему уравнений (4.2) в канонической форме записи:

Рассматривая полученную систему уравнений в виде (4.3), можно сфор-

мулировать методику формирования узловых уравнений непосредственно по схеме цепи, имеющей n1 = g – 1 независимых узлов (g – число узлов в схеме):

левая часть узлового уравнения, составленного для i-го независимого узла, есть сумма членов, один из которых равен произведению узлового напряжения i-го узла на его собственную проводимость– Yii∙Uii , а остальные – произведениям узловых напряжений других независимых узлов j на взаимные проводимости i-го и j-го узлов - Yij∙Ujj. Правая часть каждого уравнения равна узловому току соответствующего узла Jii.

Полученные результаты могут быть обобщены для произвольной линейной цепи, составленной из сопротивлений, емкостей, индуктивностей и независимых источников напряжения и тока:

Y11U11 + Y12U22 +…+ Y1NUNN = J11; Y21U11 + Y22U22 +…+ Y2NUNN = J22;

. . . . . . . . . . . . . . . .

23

токов.

Для линейной цепи, состоящей из R, L, C и независимых источников электрической энергии матрица проводимостей всегда квадратная и симметричная относительно главной диагонали, т.е. Yij = Yji.

Решая систему узловых уравнений, определяют узловые напряжения, а по ним – токи в ветвях.

Частный случай. Исследуемая цепь может содержать идеальный источник напряжения (без последовательно включенного сопротивления), включенный между двумя узлами. В этом случае один из этих узлов целесообразно принять за базисный. Тогда узловое напряжение другого узла будет равно ЭДС источника (со знаком плюс или минус), т.е. известное. Следовательно, узел, к которому подключен источник напряжения, в этом случае оказывается зависимым, число неизвестных узловых напряжений уменьшается до n1 = g – 1 – pин (pин – число идеальных источников ЭДС). Узловые уравнения формируются только для узлов, к которым не подключены источники напряжений. В левой части равнений в первоначальной их записи учитываются все узловые напряжения, как известные, так и неизвестные, но затем члены, содержащие известные узловые напряжения, переносят в правую часть уравнений.

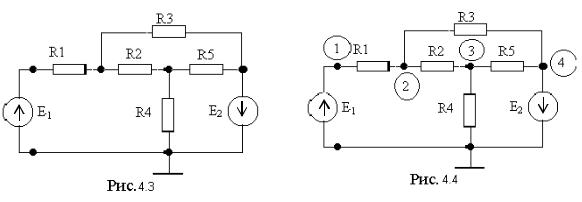
Пример 4.2. Используя метод узловых напряжений, составить уравнения электрического равновесия цепи, схема которой приведена на рис.4.3.

24

Решение. Будем считать, что точка соединения источника E1 с сопротивлением R1 образуют входной узел цепи. Схема содержит g = 5 узлов и два независимых источников напряжения. Каждый из них включен между узлами без сопротивления. Примем один узел, объединяющий полюса источников, за базисный, а остальные узлы пронумеруем, как показано на рис.4.4.

К узлам 1 и 4 подсоединены источники напряжений, поэтому их узловые напряжения равны ЭДС с соответствующим знаком: U11 = E1, U44 = –E2. Для этих узлов уравнения составлять не надо. Поэтому система уравнений будет содержать не четыре, а два уравнения для второго и третьего узлов. Запишем уравнения по первому закону Кирхгофа по методике, изложенной в примере

4.1:

–E1·g1 + U22·(g1 + g2 + g3) – U33·g2 + E2·g3 = 0,

–U22·g2 + U33·(g2 + g4 + g5) + E2·g5 = 0.

Перенесем известные члены в правую часть уравнений и запишем эту систему в матричной форме

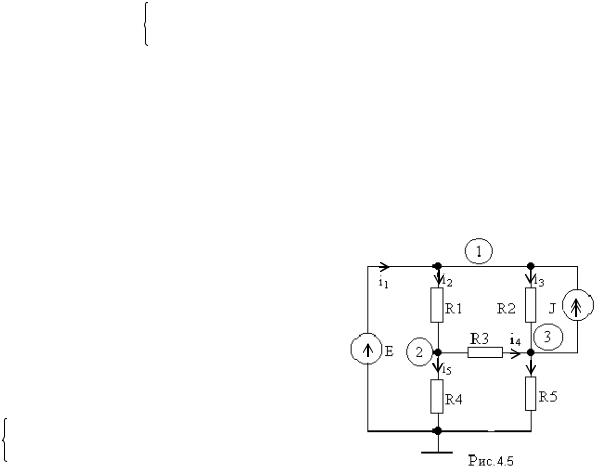
Пример 4.3. Определить токи методом узловых напряжений в ветвях цепи, схема которой изображена на рис.4.5.

R1 = R3 = 10 Ом; R2 = R4 = 20 Ом; R5 = 30 Ом; J = 1 A; E = 10 В.

Решение.

1. Пронумеруем узлы, выбрав один из них за базисный (см. рис.4.5).

2. К первому узлу подключен источник

окончательном виде

5. После подстановки численных значений параметров и решения уравнений, получим

U22 = 3.7209 В, U33 = –0.6977 В. 6. Определим токи в ветвях:

25

i2 = (E – U22)g1 = 0.628 А; i3 = (E – U33)g2 = 0.535 А;

i4 = (U22 – U33)g3 = 0.442 А; i5 = U22g4 = 0.186 А; i6 = U33g5 = – 0.023 А.

i1 = i2 + I3 – J = 0.163 А (по первому закону Кирхгофа для первого узла).

7. Проверим правильность решения задачи, используя закон Кирхгофа для второго узла: –i2 + i4 + i5 = 0, – 0.628 + 0.442 + 0.186 = 0. Задача решена правильно.

Определение токов в этой задаче потребовало решения системы из двух уравнений. Этот же пример рассматривался при изучении методов токов ветвей и контурных токов.

Сравнивая три метода расчета по сложности решения задач по определению токов ветвей, контурных токов и узловых напряжений, можно придти к следующему выводу:

при анализе сложной цепи методы контурных токов и узловых напряжений позволяют уменьшить число уравнений по сравнению с методом токов ветвей. Выбор метода контурных токов или узловых напряжений опреде-

ляется наименьшим количеством независимых контуров или узлов.

Следовательно, выбирать метод нужно после проведения топологического анализа схемы по наименьшему количеству независимых контуров или узлов.

На основе решения одной и той же задачи в примерах 3.3 и 4.3 разными методами видно, что проще эту задачу решить методом узловых напряжений.

26

ТЕМА 5. РАСЧЕТ ЛИНЕЙНЫХ ЦЕПЕЙ, СОДЕРЖАЩИХ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ

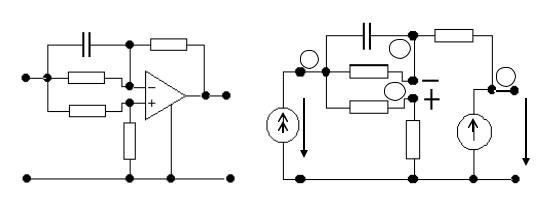
Идеальным операционным усилителем (ОУ) называется идеальный источник напряжения, управляемый напряжением (ИНУН), с бесконечно большим коэффициентом усиления k → ∞. Входные токи ОУ равны нулю.

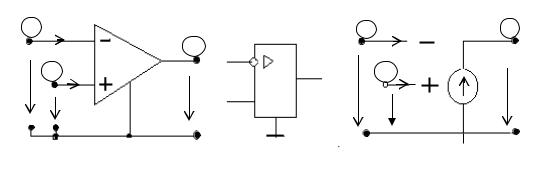
На рис. 5.1 показано уловное графическое изображение идеального (а), реального (б) ОУ и его схема замещения (в).

Усилитель имеет две пары входных полюсов (1 – 0) и (2 – 0) и выходные полюса (3 – 0). Особенность ОУ состоит в том, что выходное напряжение U3

пропорционально разности напряжений на входных зажимах U1, U2, а входные

управляемым источником напряжения e = ƒ(U1, U2) = k·(U2 – U1). Если соединить между собой входные зажимы (2 – 0), т.е. U2 = 0, то, как следует из выражений (5.1), ОУ ведет себя как инвертирующий усилитель т.е U3 = –k∙U1 – выходное напряжение отличается от входного по фазе на 1800. При соединении между собой зажимов (1 – 0) т.е. U1 = 0, ОУ ведет себя как не инвертирующий усилитель U3 = k∙U2. В связи с этим, зажимы (1 – 0) называются инвертирую-

щими, а зажимы (2 – 0) – не инвертирующими входами. На графических изображениях ОУ инвертирующий вход обозначен знаком «–» или кружком, не инвертирующий – «+». Эти знаки не указывают на полярность соответствующих напряжений.

При анализе схем, содержащих ОУ, следует учитывать основное свойство ОУ, вытекающее из (5.1):

– при конечном значении выходного напряжения Uвых = U3 и бесконечно большом коэффициенте усиления k разность (Uвх2 – Uвх1) должна стремится к

27

нулю, т.е. зажимы 1 и 2 должны иметь одинаковый потенциал φвх1 = φвх2 = Uвх1

= Uвх2. Это допущение, а также учет того, что входные токи ОУ равны нулю, позволяют существенно упростить анализ цепей с ОУ.

В некоторых случаях один из входов ОУ бывает соединен с базисным узлом, например U2 = 0. Тогда U3 = – k∙U1 и при k = ∞ U1 = 0.

Расчет цепей с ОУ можно проводить любым методом анализа, однако результаты расчета с учетом сформулированного свойства ОУ получаются проще при использовании метода узловых напряжений.

Рассмотрим методику формирования узловых уравнений цепи, содержащей ОУ, при решении конкретной задачи.

Пример 5.1. Найти операторный коэффициент передачи по напряжению цепи, схема которой изображена на рис. 5.2 а.

Решение. Задачу решим методом узловых напряжений. Для этого включим на входе цепи идеальный источник тока J, пронумеруем независимые узлы и заменим изображение ОУ схемой замещения. Полученная схема цепи изображена на рис. 5.2 б.

Между четвертым и базисным узлами включен идеальный источник напряжения e = U44. Поэтому узел 4 является зависимым и для него уравнение по первому закону Кирхгофа не составляем. Однако для этого узла необходимо использовать основное уравнение ОУ (5.1), которое для схемы на рис. 5.2 б имеет вид:

28

Из уравнения (5.2) (четвертое в системе уравнений (5.3)) следует, что при k = ∞, U22 = U33. Поэтому в матрице проводимостей (5.3) необходимо сложить элементы второго и третьего столбцов и оставить их сумму, убрать одну переменную, например U33, и четвертое уравнение как зависимое. В результате этих преобразований получим систему уравнений в окончательном виде

Решая систему уравнений относительно U11 и U44, получим операторный коэффициент передачи по напряжению

На основании решенного примера можно сформулировать методику со-

ставления системы уравнений для цепи, содержащей идеальный ОУ методом узловых напряжений.

1.Подключить к входу цепи источник сигнала в виде идеального источника напряжения или тока.

2.Пронумеровать узлы схемы, в т.ч. входы и выход ОУ. За базисный узел всей схемы принять базисный узел ОУ. Можно не прибегать к схеме замещения ОУ, а работать с исходной схемой цепи.

3.Записать уравнение ОУ, определяющее выходное напряжение ОУ, с учетом пронумерованных входных и выходного полюсов ОУ.

4.Записать систему уравнений в матричной форме непосредственно по схеме цепи. При этом для выходного узла ОУ использовать основное уравнение ОУ.

5.Отметить номера столбцов матрицы проводимостей, соответствующих номерам входов ОУ.

6.Сложить элементы столбцов матрицы проводимостей с номерами входов ОУ и оставить вместо этих двух столбцов столбец с суммами. Вычеркнуть

вматрице проводимостей строку с номером выхода ОУ. Убрать из системы одно узловое напряжение с номером входа ОУ и строку в матрице – столбце узловых токов.

7.Записать систему уравнений после проведенных преобразований.

8.Вычислить необходимые узловые напряжения схемы.

Частный случай. Если цепь содержит ОУ с одним входом (другой соединен с базисным узлом), то нужно вычеркнуть столбец и узловое напряжение, номер которых соответствует номеру входа ОУ.

29

Пример 5.2. Получить формулу коэффициента передачи по напряжению цепи, в которой используется типовая схема включения ОУ (рис. 5.3 а).

Рис.5.3

Решение. 1. Подключим к входу цепи идеальный источник тока J. Пронумеруем узлы. Как рекомендовалось ранее, не будем заменять изображение ОУ схемой замещения. Выполнение этого пункта показано на рис. 5.3 б.

2. Запишем основное уравнение ОУ для схемы на рис. 5.3 б

U33 = –k∙U11 или k∙U11 + U33 = 0. (5.5)

3. Составим систему уравнений в матричной форме для цепи на рис. 5.3 б (5.6). При этом нужно помнить, что выходная цепь ОУ представлена идеальным источником напряжения, подключенным к третьему узлу. Для этого узла уравнение по первому закону Кирхгофа не составляют, а используют уравнение ОУ (5.5)

4. Из уравнения (5.5) видно, что при k = ∞ U22 = 0. Поэтому в матрице проводимостей нужно вычеркнуть второй столбец и третью строку. Вычеркнуть переменную U22 и третью строку в матрице токов. После проведенных преобразований получиться система уравнений в следующем виде:

Коэффициент передачи по напряжению цепи равен

Решая систему уравнений (5.7) и подставляя узловые напряжения в (5.8), получим

30