1491

Следует отметить, что в данной модели не учтено насыщение магнитной цепи, что может быть реализовано путем коррекции индуктивности взаимоиндукции по продольной оси в функции тока намагничивания на каждом шаге интегрирования. Данный вопрос является предметом дальнейших исследований.

Список литературы

1. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем в MATLAB 6.0: учеб. пособие. – СПб.: КОРОНА принт, 2001.

2.Черных И.В. Моделирование электротехнических устройств в

MATLAB, SimPowerSystems и Simulink. – М.: ДМК Пресс; СПб.: Питер, 2008. – 288 с.

3.Ха Ань Туан. Адаптивное управление мощным синхронным генератором: дис. ... канд. техн. наук. – СПб., 2014. – 116 с.

4.Математическая модель явнополюсного синхронного генератора миниТЭЦ / Г.Я. Вагин, Е.Б. Солнцев, А.М. Мамонов, А.А. Петров // Инженерный вестник Дона. – 2015. – № 2.

Введение

Прикладная задача управления шагающими роботами встречается во многих областях деятельности человека, например в робототехнике, на транспорте, в медицине.

Яркий пример шагающих роботов – экзоскелет. Экзоскелеты являются одним из эффективных устройств для компенсации, восстановления или усиления двигательной способности человека. Их эффективность во многом определяется успешностью решения двух научнотехнических задач:

1. Получение подробной математической модели динамики движения экзоскелета, учитывающей:

–взаимосвязанность динамики движений по степеням подвижности;

–взаимозависимость электромагнитных и механических процессов в приводах.

2. Построение управления экзоскелетом с учетом особенностей его динамики и требований биомеханики.

Авторами представлен процесс построения компьютерной модели динамики движения пятистепенного экзоскелета с учетом взаимосвязанности движений по степеням подвижности. Рассматривается только механизм экзоскелета. Такая модель позволяет воспроизводить динамику ходьбы человека, что, в свою очередь, даст возможность строить эффективное управление экзоскелетами.

Описание экзоскелета как объекта управления

На рис. 1 изображены модель и схема двуногого экзоскелета, который содержит жесткие инерционные элементы: корпус и две одинаковые ноги. Каждая нога имеет две степени подвижности – бедро и голень.

Введем следующие обозначения: mk, ma, mb – масса корпуса, бедер,

голеней;

lk, la, lb – длины корпуса, бедер, голеней;

rk, ra, rb – расстояние от тазобедренного сустава, коленного сустава до центра масс корпуса, центра масс бедра, центра масс голени;

jk, ja, jb – момент инерции корпуса, бедер, голеней;

g – ускорение силы тяжести;

R1, R2 – внешние силы, приложенные к концам А1, А2 ног.

Рис. 1. Модель и схема двуногого экзоскелета

Пусть OXYZ – неподвижная прямоугольная система координат. Предполагаем, что экзоскелет движется вдоль оси OX в плоскости OXY.

Данный экзоскелет имеет пять степеней свободы. Выберем вектор обоб-

щенных координат q = [ψ, α1, α2, β1, β2] – углы, которые образуют звенья с вертикалью, где Ψ – угол между корпусом

ивертикалью; αi – углы между бедрами

ивертикалью; βi – углы между голенями

ивертикалью; ui, ki – управляющие моменты.

Уравнения движения и динамические характеристики

Уравнения движения изучаемого экзоскелета построим на основе уравнений Лагранжа второго рода [1–5]:

где q – вектор обобщенных координат; Q – вектор обобщенных сил; T – кинетическая энергия; P – потенциальная энергия; L – функция Лагранжа, L = T – P.

Кинетическая энергия в обобщен-

5

ных координатах имеет вид T = ∑Ti ,

i=1

для i-го звена кинетическая энергия вы-

Потенциальную энергию системы

где M – масса механизма, М = = mk +2ma +2mb ; x, y – декартовы координаты точки подвеса ног:

x= xA1 −la sin α1 +lb sin β1 =

=xA2 −la sin α2 +lb sin β2 , y = yA1 −la cos α1 +lb cosβ1 =

=yA2 −la cos α2 +lb cosβ2.

Обобщенные силы Qi найдем из элементарной работы δW всех сил, приложенных к системе:

Qψ = −k1 −k2 ,

Qαj = −u j +k j −la (Rjx cos αj + Rjy sin αj ),

Qβj = −u j +lb (Rjx cosβj + Rjy sin βj )

(j = 1, 2).

Система дифференциальных уравнений Лагранжа второго рода для пятистепенного экзоскелета:

Qψ = Jrψ− gKr sin ψ− −Kr (x cos ψ+ y sin ψ),

Qαj = Jaαj + Ka (x cos αj + y sin αj )+

+gKa sin αj +

+Iab βj cos(αj −βj )−β2j sin (αj −βj ) ,

Qβj = Jββj + Kb (x cosβj + y sin βj )+

+gKb sin βj +

+Iab αj cos(αj −βj )−α2j sin (αj −βj ) ,

Ia = Ja +la2mb , Ka = ra (ma +2mb ),

Kb = rbmb , Iab = 2rarbmb (j = 1, 2).

Координаты центра масс механизма хс, ус имеют следующие выражения [1]:

Mxc = Mx −mk rk sin ψ +

2

+ ∑(mara sin αj +mbrb sin βj ),

j=1

Myc = My −mk rk cos ψ+

2

+ ∑(mara cos αj +mbrb cosβj ).

j=1

Уравнение движения центра масс механизма можно записать так:

Mxc = R1x + R2x ,

Myc = R1y + R2 y −Mg.

Уравнения управляющих моментов на суставах робота вычисляются как [3]

k j = F1 j +ui −la (Rjx cos αj + Riy sin αj ),

u j = F2 j −lb (Rjx cosβj + Riy sin βj ),

F1 j = (Ja +la2mb )a j +

+Ka (x cos αj + y sin αj )+

+gKa sin αj +

+Iab βj cos(αj −βj )+β2j sin (αj −βj ) ,

F2 j = Jbβj + Kb (x cosβj + y sin βj )+

+gKb sin βj +

+Iab αj cos(αj −βj )+α2j sin (αj −βj ) .

При одноопорной фазе ходьбы, на-

пример если первая нога (j = 1) является опорной ногой, R2x = R2y = 0 и мы можем вычислить управляющие моменты в суставах робота.

Однако при двухопорной фазе определение этих моментов неоднозначно. Для определения восьми неизвестных Rjx, Rjy, kj, uj (j = 1, 2) мы располагаем только пятью уравнениями. Необходимо доопределить часть неизвестных (полуобратный метод), например можно задать реакцию силы одной из двух опор [6] следующим образом:

R2x = a1 +a2t +a32t2 ,

R2 y = b1 +b2t +b32t2 ,

где a1, a2, a3, b1, b2, b3 – коэффициенты, определенные из параметров времени и желаемых состояний механизма в конце двухопорной фазы.

Компьютерное моделирование движения пятистепенного экзоскелета

Одноопорная фаза

Будем моделировать движение одного шага пятистепенного шагающего робота в одноопорной фазе (т.е. R2x, y = 0)

по методу интерполяции с заданными необходимыми условиями:

–T – время одного шага;

–∆x – длина шага;

–L0 – расстояние от тазобедренного сустава до оси OX при t = 0;

–∆h(t) – высота конечной точки A2 переносимой ноги над опорной поверхностью в функции времени;

–начальное и конечное состояния в пределах одного шага: q(0) = –q(T);

При заданной длине шага угол отклонения ног от вертикали вычисляется

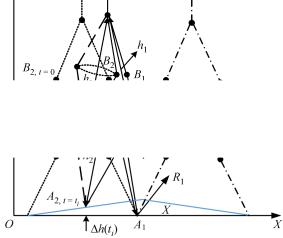
[α1(ti), β1(ti)] и высота точки A2 переносимой ноги ∆h(ti). Остальные координаты переносимой ноги находятся следующим образом: строятся две окружности с центрами O2, A2 и радиусами la, lb соответственно. Тогда точки пересечения этих окружностей определяют возможные положения голени переносимой ноги.

Введем следующие обозначения: h1, h2 – расстояния от тазобедренного сустава до точек A1, A2 (рис. 2).

Рис. 2. Одноопорная фаза

Из множества корней точки пересечения B2 получим таблицу данных движения коленного сустава, из которой интерполяцией по методу наименьших квадратов получим координаты коленного сустава в функции времени.

Двухопорная фаза

Примем ряд условий, которые изложены в работе [5]:

– Соотношение между двумя фазами

4:1.

–Задняя нога совершает отталкивание тела вперед, а передняя нога осуществляет торможение.

–Диапазон изменений углов в суставах задней ноги составляет: в колен-

ном суставе ∆KC = 12…15°, в опорной точке ∆OT = 8…12°.

– Максимум продольной составляющей главного вектора реакции опоры может достигать 0,25P.

Для того чтобы интерполировать обобщенные координаты задней ноги,

возьмем базисные функции: F (t, a0 , a1 ) = = a1 sin(ωt) +a2 cos(ωt), где ω= 0,22πT .

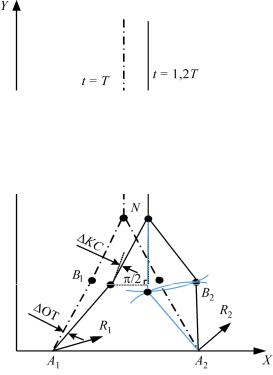
На промежутке ∆t = 0,2Т от конечного состояния [α1(T), β1(T)] одноопорной фазы с указанными условиями получены

Рис. 3. Двухопорная фаза

координаты задней ноги как функции времени.

Движение точки подвеса ног описывается следующими уравнениями:

xN (t) = xA1 +lb sin β1 +la sin α1, yN (t) = yA1 +lb cosβ1 +la cos α1,

где xA1 , xA2 – константы, yA1 , yA2 = 0.

Функции времени передней ноги [α2(t), β2(t)] определяются аналогично

(рис. 3).

Заключение

Представленный подход к построению модели динамики движения пятистепенного экзоскелета учитывает взаимосвязь динамики движений механизма по степеням подвижности и позволяет построить динамическую модель движения, подобного ходьбе человека.

Такая модель даст возможность реализовать эффективное управление ходьбой экзоскелета, включая управление в статически неустойчивых положениях.

Всё это существенно повысит эффективность применения экзоскелетов во многих областях деятельности человека, в частности в реабилитационной медицине.

Список литературы

1.Формальский А.М. Перемещение антропоморфных механизмов. – М.:

Наука, 1982. – 368 с.

2.Белецкий В.В. Двуногая ходьба. –

М.: Наука, 1984.

3.Бербюк В.Е. Динамика и оптимизация робототехнических систем. – Ки-

ев: Наук. думка, 1989. – 192 с.

4.Вукобратович М. Шагающие роботы и антропоморфные механизмы. –

М.: Мир, 1976. – 541 с.

5.Дубровский В.И., Федорова В.Н., Биомеханика. – M.: Владос-пресс, 2003. – 672 с.

Исследуется задача локальной стабилизации, когда маятник находится в некоторой малой окрестности режимной точки. В частности, в отсутствие управления (L = 0) уравнение (2) имеет тривиальное решение

Линеаризуем уравнение (2) около состояния равновесия (4), тогда получаем (при F = 0) уравнение движения маятника следующего вида:

отвечающее неустойчивому положению равновесия неуправляемого маятника с обоими перевернутыми звеньями. Характеристическое уравнение однородной системы (5) имеет вид

(a a −a2 )λ2 −

11 22 12 (6) − (a11b2 + a22b1 )λ+b1b2 = 0.

При помощи невырожденного преобразования

где K – постоянная матрица, уравнение

(5) может быть приведено к уравнению с координатам x1, x2 , т.е. к виду [2]

Матрица преобразования K состоит из собственных векторов матрицы A0−1B.

Она может быть выбрана, например, в следующем виде:

Матрица преобразования к нормальным координатам может отличаться

от вида (9). Если матрицу преобразования выбрать в виде (9), то [2]

d= dd1 = K−1A0−1 =

2

Система (8) эквивалентна двум скалярным дифференциальным уравнениям, записанным в координатах х1 и х2:

x1 −λ1x1 = d1L, x2 −λ2 x 2 = d2 L. (11)

Здесь

× b1 −(a11 +a12 )λ1 .−b1 +(a11 +a12 )λ2

Столбцы получены при помощи выражения (10).

Спектр системы (11) содержит два положительных собственных значения:

µ1 = λ1 , µ2 = λ2 (µ1 > µ2 > 0), (12)

и два равных им по абсолютной величине отрицательных −µ1, −µ2.

b2 −(a11 +a12 )λ2 = 0. Подставив значение

ние (6), получаем, что эти равенства могут иметь место при условии

(a12 +a22 )b1 = (a12 +a11 )b2 , и только при

нем. Если же последнее равенство не имеет места, то b1 −(a11 +a12 )λ1 ≠ 0. При

этом d1 ≠ 0, d2 ≠ 0, и механическая сис-

тема (11), а значит, и исходная (5) полностью управляемы [4] при наличии управляющего момента только в межзвенном шарнире.

Управляемая линейная система (5) имеет два положительных собственных значения (12) µ1 > µ2 > 0. Обозначим че-

рез Q область управляемости. Чтобы построить область Q для системы (11),

представим систему четвертого порядка в жордановой форме и выделим два дифференциальных уравнения первого порядка, отвечающие положительным собственным значениям (12).

Жордановы переменные y1, y2 связаны с собственными значениями µ1, µ2

При управлении L(t) = −L0 система

(13) имеет тоже стационарную и неустойчивую точку

Область с множеством начальных состояний Q ограничена по «неустойчивым» переменным у1 и у2. По двум другим жордановым переменным у3 и у4, которые отвечают отрицательным собственным значениям −µ1, −µ2 , область

управляемости не ограничена, т.е. она представляет собой цилиндрическое

множество. Сечение S этой области плоскостями y3 = 0, y4 = 0 – открытое

множество, симметричное относительно начала координат

Множество S – область управляемости системы (13), т.е. множество начальных состояний y1(0), y2 (0), из которых

система (13) может быть приведена в начало координат (14) при помощи управления L(t) U. Граница этого множества состоит из двух симметричных относительно начала координат интегральных траекторий системы (13), которые получаются при L(t) = L0 и при

L(t) = −L0. Одна из этих траекторий, построенная при L(t) = L0 , начинается при

t = 0 из точки (15), а при t → ∞ заканчивается в точке (14). Ее уравнение имеет вид

Другими словами, траектория (18) начинается при t → −∞ из точки (15) и заканчивается при t = 0 в точке (14). В точках (14) и (15) граничные траектории (15), (16) «смыкаются» и они являются угловыми точками области S.

Пример. При параметрах маятника

L = −(g1ϕ1 + g2ϕ1 + g3ϕ2 + g4ϕ2 ) с коэф-

фициентами g1 = 12; g2 = 3; g3 = 0,0017; g4 = 0,0126 система достигла вертикального положения за 3 с.

На рисунке показаны графики переходных процессов перевернутого маятника.

а

б

Рис. Графики переходных процессов перевернутого маятника: а – движение первого звена маятника в верхнее положение; б – производная процесса движения

На основании проведенного исследования можно сделать следующие выводы:

При ограниченном управляющем моменте область управляемости (начальных значений) линеаризованной системы ограничена по двум «неустойчивым» жордановым переменным.

Построение области управляемости позволяет оценить сверху область притяжения, которая может быть реализована при синтезе обратной связи управления.

Если в каждом из двух шарниров двухзвенного маятника приложить ограниченный управляющий момент, то область управляемости системы увеличивается, хотя и остается ограниченной.

Зная область S, можно оценить сверху области притяжения для любого вида обратной связи, ограниченной неравенством (3).

Список литературы

1.Формальский А.М. Управляемость и устойчивость систем с ограниченными ресурсами. – М.: Наука, 1974. – 368 с.

2.Формальский А.М. Управление движением неустойчивых объектов. –

М.: Физматлит, 2014. – 232 с.

3.Летов А.М. Устойчивость нелинейных регулируемых систем. – М.:

Физматлит, 1962.– 484 с.

4.Габриелян М.С., Красовский Н.Н.

Кзадаче о стабилизации механической системы // Прикладная математика и ме-

ханика. – 1964. – Т. 28, вып. 5. – С. 801– 810.

5.Формальский А.М. Об угловых точках границ областей достижимости // Прикладная математика и механика. – 1983. – Т. 47, вып. 4. – С. 556–574.