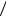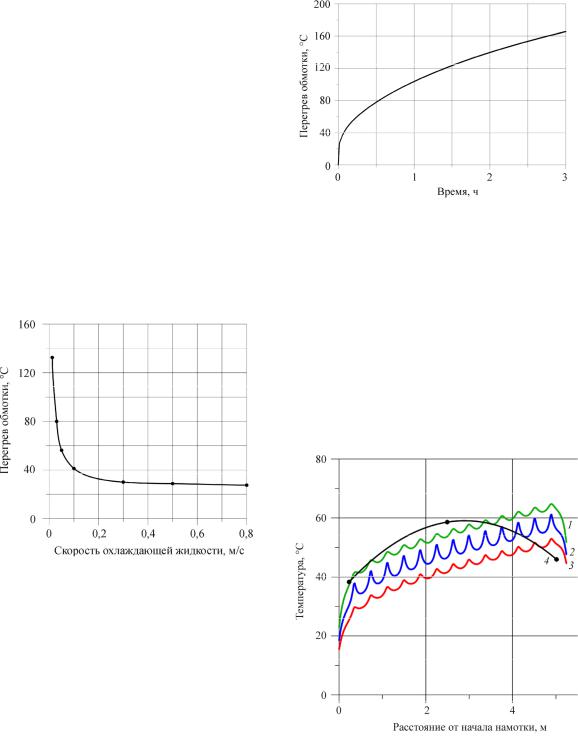
стационарным уравнением теплопроводности: с объемным источником тепла в проводниках (внутри ПЭД) и с членом, учитывающим перенос тепла движущейся жидкостью – в кольцевом зазоре вокруг ПЭД. Ламинарное течение в зазоре описывали уравнениями Навье–Стокса, турбулентное – уравнениями Рейнольдса, для замыкания которых использовали SST-модель турбулентности. Проведенные расчеты позволили спрогнозировать некоторые новые явления и объяснить уже известные. Так, было показано, что если фиксировать мощность, потребляемую ПЭД, и увеличивать скорость охлаждающей жидкости, то перегрев сначала уменьшается, затем стабилизируется на некотором уровне и потом слабо зависит от скорости охлаждающей жидкости
(рис. 7).
лялся в основном по механизму теплопроводности. Затем формировался существенно более быстрый механизм конвективного переноса тепла.
Рис. 8. Зависимость среднего перегрева обмотки ПЭД 32-117 от времени
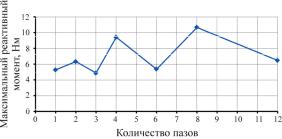
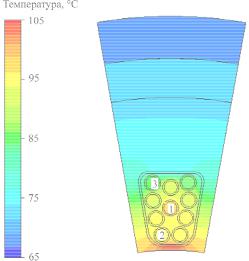
Было показано, что распределение температуры по длине ПЭД (рис. 9) немонотонно: в области промежуточных подшипников выше на 1–3 град. В сечении паза плоскостью перпендикулярной оси неоднородность температуры внутри паза составляет примерно 10 °С (рис. 10).
Рис. 7. Зависимость перегрева обмотки ПЭД 63-117 от скорости охлаждающей жидкости (u = 0,05 м/с)
Перегрев изоляции в условиях от- |
|
сутствия прокачки охлаждающей жидко- |
|
сти в затрубном пространстве сущест- |
|
венно неоднороден во времени (рис. 8): в |
|
первые ~ 15 мин температура нарастает |
Рис. 9. Распределение температуры длине ПЭД: |
заметно быстрее, чем в последующие. |
Это происходило потому, что сначала |
1–3 – в проводниках; 4 – экспериментальные |
данные |
жидкость между ПЭД и обсадной колон- |
|
ной неподвижна и теплоотвод осуществ- |
|
|
242 |
УДК 621.313.333.01-213.32
ЭЛЕКТРОМАГНИТНЫЙ РАСЧЕТ ПОГРУЖНОГО АСИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ
Е.В. Пошвин1, А.С. Фадейкин1, С.Н. Пещеренко2
1 АО «Новомет-Пермь»
2 Пермский национальный исследовательский политехнический университет
На основе решения уравнений Максвелла вычислены рабочие характеристики ряда типичных погружных электродвигателей. Показано, что предел повышения КПД серийных электродвигателей составляет примерно 4–5 % за счет увеличения коэффициента заполнения пазов статора, уменьшения магнитных потерь железа и уменьшения зазора статор – ротор до значений, близких к предельно допустимым.
Ключевые слова: расчет асинхронного электродвигателя, уравнения Максвелла, метод конечных элементов.
ASYNCHRONOUS MOTOR ELECTROMAGNETIC CALCULATION
E.V. Poshvin1, A.S. Fadeikin1, S.N. Peshcherenko2
1 JSC “Novomet-Perm”
2 Perm National Research Polytechnic University
Relying on Maxwell’s equations solution operational characteristics for a variety of typical submersible electric motors were calculated. It is shown, that serial motor efficiency can be raised by 4-5% by means of increasing the stator slot filling coefficient, reducing magnetic iron losses and reducing the stator-to-rotor gap near to the their ultimate values.
Keywords: asynchronous motor calculation, Maxwell's equations, finite element method.
Введение
Потери энергии в погружном асинхронном электродвигателе (ПЭД) составляют более 15 %. Среди компонентов погружной установки ПЭД является вторым, после насоса, узлом по потерям энергии.
В течение десятилетий применения асинхронных ПЭД были приняты все меры для повышения его КПД и коэффициента мощности: совершенствовались методики расчета и проектирования, использовались высококачественные электротехнические стали для магнитопровода, термостойкая электроизоляция, модернизировались подшипники. Эти меры позволили достичь значений КПД, по-видимому, близких к максимально возможным для асинхронных ПЭД, и за последние 10 лет КПД
практически не изменялся [5, 7]. Так, величина КПД лучших образцов самого распространенного в мире асинхронного ПЭД габарита 117 мм не превышает 86 %, а значение коэффициента мощности не превышает 0,87.
В связи с этим можно предположить, что асинхронные ПЭД, работающие при частоте питания от 40 до 70 Гц, исчерпали свои возможности по увеличению КПД и коэффициента мощности. Дальнейшая модернизация асинхронных ПЭД с целью улучшения энергетических показателей технически сложна и экономически нецелесообразна.
Целью данной работы стала проверка этого утверждения. Были решены следующие задачи:
− разработана методика имитационного моделирования рабочего процесса ПЭД;
|
Тестовые примеры: расчет |
для ПЭД 100-117 – на рис. 6, 7 и в |
|
нескольких типичных ПЭД |
табл. 2, для ПЭД 400-185 – на рис. 8, 9 и |
|
Были проведены расчеты основных |
в табл. 3. Видно, что расхождение экспе- |
|
рабочих характеристик трех погружных |
риментальных и расчетных данных для |
|
электродвигателей: ПЭД 63-103, ПЭД |
ПЭД 63-103 составляет 2–3 %, для ПЭД |
|
100-117, ПЭД 400-185 (первая цифра – |
100-117 – 1–6 %, для ПЭД 400-185 – 4–6 |
|
%. В связи с этим можно утверждать, |
|
мощность, кВт, вторая – внешний диа- |
|
метр корпуса, мм). |
что разработанная методика электроме- |
|
Полученные результаты для ПЭД |
ханического расчета ПЭД имеет относи- |
|
63-103 приведены на рис. 4, 5 и в табл. 1, |
тельную ошибку не более 6 %. |
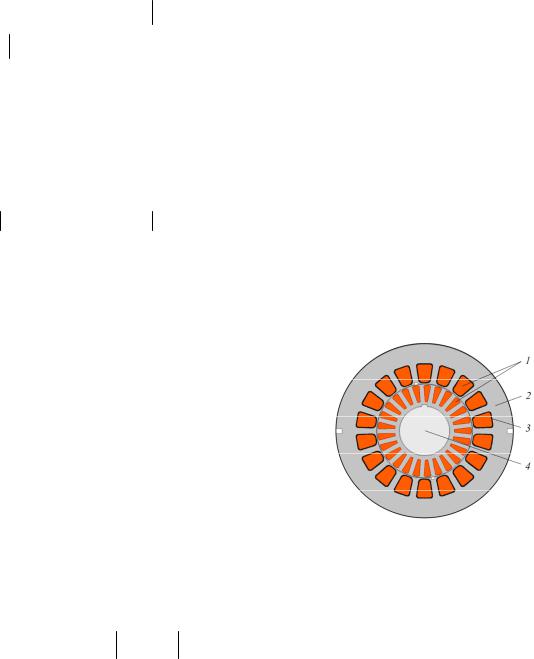
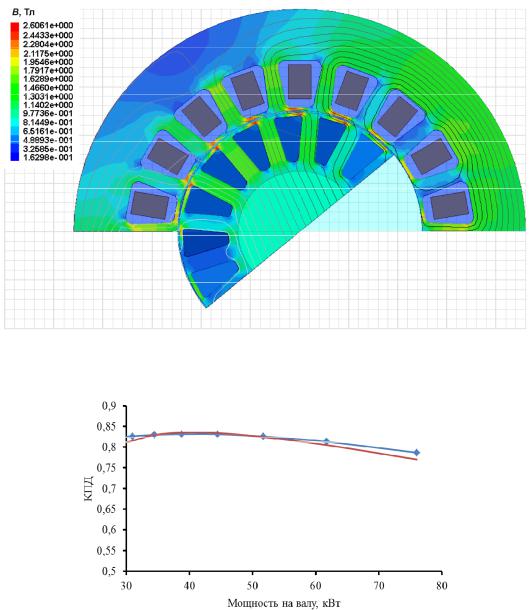
Рис. 4. Поле магнитной индукции в ПЭД 63-103
Рис. 5. Зависимость КПД от выходной мощности для ПЭД 63-103:  эксперимент;
эксперимент;  расчет
расчет
249
|
|
|
Таблица 1 |
Расчет характеристик ПЭД 63-103 |
|
|
|
|
|
|
Характеристики |
Экспериментальные |
Расчет |
Отн. ошибка, |
|
данные |
|
% |
Потребляемая мощность при номинальной |
|
|
|
нагрузке, кВт |
77,2 |
78,75 |
2,1 |
Номинальный ток, А |
31,9 |
32,8 |
2,8 |
КПД при номинальной нагрузке, % |
81,6 |
80,0 |
2,0 |
Ток холостого хода, А |
18,7 |
18,0 |
3,0 |
Рис. 6. Поле магнитной индукции в ПЭД 100-117
Рис. 7. Зависимость КПД от выходной мощности для ПЭД 100-117:  эксперимент;
эксперимент;  расчет
расчет
250



 эксперимент;
эксперимент;  расчет
расчет
 эксперимент;
эксперимент;  расчет
расчет