
Математическое моделирование в естественных науках
..pdf
абсцисс, V – радиальная компонента вектора скорости, P – давление, E – удельная внутренняя энергия, k – показатель адиаба-
ты, J – потенциальная энергия, J = E − U 2 + V 2 ; W – вектор
2
скорости, αi – концентрация i-й фазы, τr,x – функции силового межфазного взаимодействия, q – функция теплового межфазного взаимодействия, ρ1u – истинная плотность 1-й фазы.
Система уравнений (1)–(6) решалась численно методом крупных частиц (метод Давыдова) [2, 3]. В рамках данного метода сплошная среда заменяется конечно-разностной сеткой. Основная идея заключается в расщеплении по физическим процессам исходной системы дифференциальных уравнений в частных производных.
В качестве граничных условий были заданы условия непротекания на границе трубы. Начальные условия задавались в зависимости от газа, находящегося в зоне высокого и низкого давлений, начальные скорости были нулевыми.
Для решения поставленной задачи метод крупных частиц был реализован в виде программы для ЭВМ, при помощи которой был проведён ряд численных экспериментов. В результате была оценена степень влияния области с высокой долей крупинок песка, в зависимости от их концентрации и протяжённости соответствующей зоны на параметры течения.
Список литературы
1.Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. – М.: Наука: Гл.
ред. физ.-мат. лит-ры, 1966. – 687 с.
2.Давыдов Ю.М., Давыдова И.М., Егоров М.Ю. Совершенствование и оптимизация авиационных и ракетных двигателей. – М.: Изд-во Нац. акад. приклад. наук России, 2002. – 303 с.
3.Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. – М.: Наука: Гл. ред. физ.-мат. лит-
ры, 1982. – 392 с.
71
ЧИСЛЕННЫЙ РАСЧЕТ ГАЗОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ВСВОБОДНОМ ОБЪЕМЕ БАЛЛИСТИЧЕСКОЙ УСТАНОВКИ
СУЧЕТОМ ДВИЖЕНИЯ СНАРЯДА
Н.Ю. Брагин, В.А. Девяткин, П.В. Писарев
(Пермский национальный исследовательский политехнический университет Пермь, Россия, nikolaybragin1409@mail.ru)
В рамках данной работы, были разработаны физические и математические модели, учитывающие характерные особенности газодинамической системы «твердотопливный заряд – свободный объем артиллерийской установки – подвижный снаряд – свободный объем канала ствола артиллерийской установки». Отработана методика численного расчета газодинамических характеристик в свободном объеме баллистической установки с учетом движения снаряда. Проведена верификация разработанных моделей.
Ключевые слова: энергетическая установка, численное моделирование, баллистическая установка, газодинамические характеристики, подвижное тело.
Повышение энергетических характеристик и качества артиллерийских установок требует уточнения методик расчета, более комплексного учета особенностей конструкции и рабочего процесса. В некоторых случаях необходимо решение связанных задач, например, с учетом движения снаряда. В данной работе рассматривается первый этап решения таких задач, а именно численный расчет газодинамических характеристик в свободном объеме баллистической модельной установки в трехмерной постановке.
Схема баллистической установки представлена на рис. 1. При нажатии кнопки «Пуск» происходит инициирование воспламенителя, затем загорается заряд и происходит выстрел. Сигнал с датчика поступает на измерительный комплекс, усиливается и отправляется на персональный компьютер, где рас-
шифровывается и обрабатывается специальной программой. Анализ конструктивной схемы баллистической установки и
учет особенностейфункционированияданной установки позволили
72
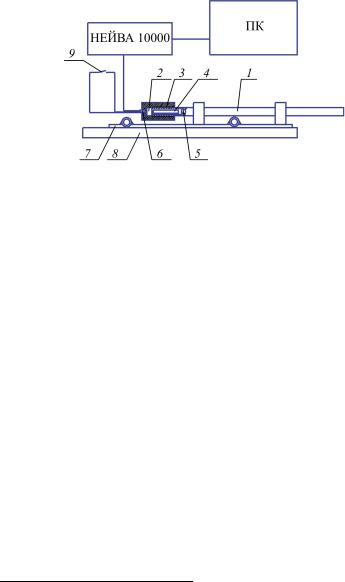
Рис. 1. Схема баллистического стенда: 1 – труба; 2 – клин; 3 – муфта; 4 – заряд; 5 – снаряд; 6 – датчик; 7 – основание; 8 – направляющие; 9 – кнопка «Пуск»
сформулировать физическую и математическую модели нестационарных газодинамических рабочих процессов в ней. При этом учитывались принятые в натурном эксперименте геометрические размеры, масса установки и снаряда, характеристики продуктов сгорания, скоростные характеристики истечения продуктов сгорания с поверхности заряда, возможность реализации турбулентного характера течения в стволе артиллерийской установки, взаимодействие продуктов сгорания и заряда, влияние окружающей среды.
На основе геометрических характеристик установки построена твердотельная модель, учитывающая характерные особенности газодинамической системы «твердотопливный заряд– свободный объем артиллерийской установки– подвижный снаряд– свободный объемканаластволаартиллерийскойустановки» (рис. 2).
В соответствии с принятыми физической и геометрической моделями разработана математическая модель, которая базируется на законах сохранения массы, импульса, энергии и замыкается уравнениями состояния идеального сжимаемого газа и турбулентности, а также начальными и граничными условиями*.
* Численное исследование актуальных проблем машиностроения и механики сплошных и сыпучих сред методом крупных частиц / под ред. Ю.М. Давыдова;
НАПН. – М., 1995.
73

Рис. 2. Схема установки со снарядом и твердотопливным зарядом: 1 – твердотопливный заряд; 2 – снаряд; 3 – свободный объем установки; а – эскиз снаряженной артиллерийской установки; б – геометрическая модель
По результатам вычислительного эксперимента были построены зависимости полного давления от времени движения снаряда в канале ствола (рис. 3) и поля распределения полного давления и векторов скорости газа в канале баллистической установки (рис. 5 и 6).
Рис. 3. График зависимости полного давления от времени движения снаряда в канале ствола
Рис. 4. Распределение полного давления в канале ствола в момент времени t = 0,0015 c
Рис. 5. Распределение векторов скорости газа в канале ствола в момент времени t = 0,0015 c
74
При анализе полученных результатов вычислительного эксперимента полученное максимальное значение полного давления совпадает с максимальным значением полного давления натурного эксперимента, а кривая зависимости P(t) повторяет кривую P(t), полученную при экспериментальном выстреле, что свидетельствует об актуальности разработаннойматематической модели.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).
РАСЧЕТ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ТОЛСТОСТЕННОГО ЦИЛИНДРА ИЗ ОРТОТРОПНОГО УПРУГОПЛАСТИЧЕСКОГО МАТЕРИАЛА ПРИ ПОМОЩИ МОДИФИЦИРОВАННОГО МЕТОДА ПЕРЕМЕННЫХ ПАРАМЕТРОВ УПРУГОСТИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Р.В. Бульбович1, В.В. Павлоградский2, П.П. Еременко3
(Пермский национальный политехнический университет, Пермь, Россия,
1dekan_akf@pstu.ru, 2rkt@pstu.ru, 3ka-ramba@mail.ru)
Рассматривается вопрос о применении метода конечных элементов (МКЭ) для определения напряженно-деформированного состояния (НДС) ортотропного упругопластическоготела на примере толстостенной трубы, нагруженной внутренним давлением. Предложена модификация обобщенного закона Гука. В качестве метода решения использован метод переменных параметров упругости. Приведены основные соотношения МКЭ изаписьмодифицированногообобщенногозаконаГука.
Ключевые слова: ортотропная упругопластичность, метод конечных элементов, метод переменных параметров упругости.
Конструкция современных ракетных двигателей на твердом топливе (РДТТ), в частности сопловых блоков, включает как металлические элементы, так и значительную часть элементов из композиционных материалов. При оценке НДС конструкции при
75
работе РДТТ чаще всего является необходимым учитывать пластические свойства материалов и их зависимость от температуры (как металлов, так и композитов).
Актуальной проблемой является моделирование упругопластических свойств композитов, которые отличаются от металлов тем, что проявляют анизотропию механических свойств, т.е. каждому направлению соответствует своя диаграмма деформирования, которая, крометого, зависитоткомпонентнапряженногосостояния.
Рассматривается второй этап решения задачи с помощью МКЭ, а именно расчет НДС тела из ортотропного упругопластического материала, результаты которого будут в дальнейшем использованы для проведения расчетов с учетом зависимости диаграмм деформирования материала не только от направления, но и от температуры.
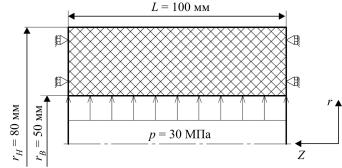
Расчет проводится для толстостенной трубы, нагруженной внутренним давлением. Задача решается в осесимметричной постановке, в статике. Схема расчетной области, ее размеры, условия закрепления и нагружения приведены на рис. 1.
В расчете используется восьмиузловой конечный элемент. Для моделирования ортотропного упругопластического поведения материала используется модифицированный обобщенный закон Гука. В качестве метода решения задачи используется метод переменных параметров упругости [1, 2].
Рис. 1. Схема расчетной области, условия закрепления и нагружения
76
Решение реализовано в виде программы на языке программирования С++ [3].
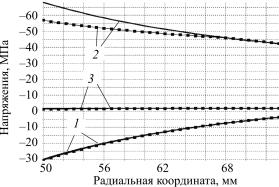
Результаты расчета программы приведены на рис. 2, на котором сплошными линиями показано решение без учета пластических свойств (т.е. для линейно-упругого ортотропного материала), линиями с маркерами – решение с использованием предложенной модификации обобщенного закона Гука.
Рис. 2. Результаты расчета программы: 1 – радиальные напряжения; 2 – окружные напряжения; 3 – осевые напряжения
Таким образом, из графиков видно, что учет пластических свойств дает при расчете снижение напряжений.
Для верификации данного метода расчета планируется проведение ряда экспериментов по нагружению трубчатых образцов внутренним давлением.
Список литературы
1.Малинин Н.Н. Прикладная теория пластичности и ползучести: учебникдля студентов втузов. – М.: Машиностроение, 1968.
2.Термопрочность деталей машин / под общ. ред. И.А. Биргера и Б.Ф. Шорра. – М.: Машиностроение, 1975.
3.Сегерлинд Л. Применение метода конечных элемен-
тов. – М.: Мир, 1979.
77
ОПИСАНИЕ НЕУПРУГОГО ДЕФОРМИРОВАНИЯ ПОЛИКРИСТАЛЛОВ С УЧЕТОМ РОТАЦИЙ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК
А.С. Ведров1, П.С. Волегов2
(Пермский национальный исследовательский политехнический университет,
Пермь, Россия, 1sanemwow@gmail.com, 2crocinc@mail.ru)
Рассматривается математическая модель неупругого деформирования поликристалла с учетом поворотов кристаллических решеток. Разработан алгоритм численной реализации модели поликристалла, учитывающей ротацию кристаллических решеток по Тейлору, а также несовместность сдвигов по системам скольжения, проведены тестовые расчеты алгоритма дляпроверкинаадекватностьпостроеннойматематическоймодели.
Ключевые слова: неупругое деформирование, поликристалл, поворот решетки, упрочнение, физические теории пластичности.
Рассмотрено моделирование неупругого деформирования поликристаллов с учетом упрочнения и поворота кристаллических решеток. Важно учитывать, что почти при любом пластическом деформировании металлические материалы испытывают изменение физико-механических свойств, что сказывается на параметрах изделий, произведенных из этих материалов. Следовательно, построение математических моделей, учитывающих изменение физико-механических свойств в процессе деформирования материала, является актуальной задачей [1].
Чтобы корректно описать эволюцию характеристик материала в процессе неупругого деформирования, необходимо знать, что является основным механизмом данного явления, атакже какими соотношениями можно описывать изменение структуры материала придействующихфизическихмеханизмахдеформации[2].
Главной задачей работы является описание хорошо известного эффекта, заключающегося в изменении ориентации кристаллографических осей зерен поликристалла в процессе интенсивной неупругой деформации. Согласованные ротации кристаллографических осей зерен в поликристалле и приводят к появлению наведенной анизотропии свойств образца [3–5]. Наиболее популярны-
78
ми моделями поворота решетки являются модель «материального поворота», модель стесненного поворота по Тейлору и модель, учитывающая несовместность сдвигов по системам скольжения. Выбор конкретной модели ротации зависит от гипотез, на основе которых строится модель: учитываются ли пластические сдвиги в зерне с некоторой ориентацией, ограничена ли деформация зерна соседями, видом нагружения и т.д.
В данной работе в качестве модели ротации выбрана модель, учитывающая несовместность сдвигов по системам скольжения, основанная на стесненном повороте по Тейлору. В качестве основных соотношений выбрано:
|
|
|
|
≡ σ − ω σ+ ω σ = п:d |
|
|
|
|
= п: (d − d |
|
|
), |
|
|
|
|||||||||||||||||||||||||||||||||||
σ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
in |
|
|
|
|
|
|||||
|
|
|
in |
|
= |
K |
(k ) |
m |
|
(k ) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
d |
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ(k ) |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(k ) |
|
|
|
|
H (τ |
(k ) |
|
|
(k ) |
),k = 1,.., K, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
γ |
|
|
|
= γ0 |
|
|
|
|
|
|
|
|
− τc |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
τc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= f ( |
|
|
|
|
|
|
|
|
|
|
|
),k, j = 1,…, K, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
(k ) |
|
γ |
( j) |
, γ |
( j) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
τc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= w − w |
|
p |
|
= w + |
1 |
|
K |
(k ) |
(n |
(k ) |
b |
(k ) |
− b |
(k ) |
n |
(k ) |
), |
(1) |
|||||||||||||||||||||||||||
ω1 |
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(m |
|
) |
m |
= |
λN × |
|
|
K |
|
|
|
n |
|
b |
|
|
|
|
|
|
|
|
K |
|
|
|
n |
|
|
b |
|
|
) N, |
|
|||||||||||||||
r |
|
|
( γ |
(i ) |
(i) |
(i) |
|
− γ |
j (m) |
j (m) |
j (m) |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и μ μ ≥ 0, |
|
|||||||||||
|
|
|
|
|
= |
A μ + |
H μ, |
при |
μ |
|
|
|
= μc |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
ω2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
μ |
r |
, в противном случае, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = ω1 + ω2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
o |
|
= ω. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
o |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В системе уравнений (1): σ,ω,d,de ,din ,o являются соответственно тензорами напряжений, спина, деформации скорости,
79
а также упругой и пластической частей тензора деформации скорости и тензором поворота КСК относительно ЛСК, ω1,ω2 – тен-
зоры спина, полученные с помощью модели стесненного поворота по Тейлору и модели, учитывающей несовместность сдвигов
по СС; μ – тензор моментных напряжений; γ(k ) , τ(ck ) – скаляры,
обозначающие скорость сдвигов и скорость изменения критических касательных напряжений по СС (для ГЦК-кристаллов количество СС равно 24), γ0 представляет базовую скорость сдвига
при равенстве касательных напряжений критическим по СС;
τ(k ) ,τ(ck ) , γ(k ) являются касательными, критическими напряжениями
инакопленным сдвигом по СС, n(i) ,b(i) ,mm – вектор нормали,
Бюргерса и вектор моментных напряжений, также N – внешняя для анализируемого объекта единичная нормаль к границе с соседним объектом, константы λ, А, Н являются параметрами материала и определяются опытным путем.
В ходе исследований рассмотрены различные варианты вида нагружения поликристалла [6], получены кривые зависимости интенсивности напряжений от интенсивности деформаций, а также траектория стереографических проекций ориентации кристаллитов.
Работа выполнена при финансовой поддержке гранта Президента РФ № МК-4917.2015.1, Российского фонда фундаментальных исследований (грант № 14-01-96008 р_урал_а).
Список литературы
1.Constitutive relations and their application to the description of microstructure evolution / P.V. Trusov, V.N. Ashikhmin, P.S. Volegov, A.I. Shveykin // Physical Mesomechanics. – 2010. – Т. 13, № 1–2. – С. 38–46.
2.Трусов П.В., Волегов П.С., Кондратьев Н.С. Физические теории пластичности: учеб. пособие. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2013. – 244 с.
80
