Основы теории цепей. Часть 2

4.6. МЕТОД ПРОСТРАНСТВА СОСТОЯНИЙ

Расчет переходных процессов в сложных электрических цепях с произвольной конфигурацией, включающей любое количество конденсаторов и катушек, весьма трудоемкий, как было показано ранее. В связи с этим большое значение имеет разработка алгоритмов, легко формализуемых и, как следствие, просто реализуемых при применении вычислительной техники. К такому методу относится метод пространства состояний (переменных состоя-

ния), который стал первым методом, позволившим алгоритмизировать формирование уравнений для электрических цепей достаточно общего вида.

Переменными состояния называют величины, число которых определяется порядком электрической цепи и значения которых достаточно для однозначного описания цепи в целом. Поскольку ток индуктивностей и напряжение на емкостях следует рассматривать как главные переменные, характеризующие состояние цепи, именно их и целесообразно выбирать в качестве переменных пространства состояния.

Обоснование выбора:

♦эти величины определяют энергетическое состояние цепи;

♦они подчиняются правилам коммутации;

♦при таком выборе уравнения состояния выглядят наиболее

просто.

Общий путь расчета переходных процессов методом пространства состояний основан на составлении n дифференциальных уравнений первого порядка относительно переменных состояния xi, записанных в канонической форме или форме Коши. Основой для формирования системы для линейной цепи служат линейные уравнения Кирхгофа и компонентные уравнения элементов цепи, поэтому такая система уравнений состояния является линейной и имеет следующий вид:

231

акции цепи) и их производных размерности n×1, где n – порядок цепи; V – матрица – столбец входных функций (воздействий) размерности m×1, где m – число входных функций; Y – матрица – столбец выходных величин (дополнительных реакций) размерностью l×1, где l – число выходных величин; A, B, C, D – матрицы связи, размерности которых соответственно (n×n), (n×m), (l×n), (l×m).

Пример. Для произвольной электрической цепи второго порядка, содержащей индуктивность и емкость, с источником тока и ЭДС, в которой необходимо определить закон изменения тока i1 (t) , уравнения состояния будут выглядеть следующим образом:

Интегрирование дифференциальных уравнений из системы (4.46) с целью определения переменных состояния и нахождения выходных величин путем решения алгебраических уравнений (4.47)

232

может выполняться различными методами. Это – аналитическое решение как в области оригиналов, так и в области изображений по Лапласу, а также аналоговое и цифровое моделирование с привлечением вычислительной техники. Цифровое моделирование, являющееся наиболее предпочтительным особенно для систем высокого порядка, основано на численном интегрировании с применением метода Эйлера, которое предполагает квантование интервала интегрирования на одинаковые отрезки (шаг интегрирования) и замену операции диф-

ференцирования отношением конечных разностей ∆x , если величи-

∆t

на шага интегрирования ∆t . Тогда производная в конце n-го шага может быть представлена следующим образом:

x& = xn+1 − xn .

n ∆t

Уравнение (4.46) на n-м шаге квантования x&n = Axn + Bvn .

Значение переменной x на (n + 1)-м шаге квантования xn+1 = x&n ∆t + xn =[ Axn + Bvn ]∆t + xn .

В результате преобразований получают рекуррентное соотношение

которые по правилам коммутации берутся равными в момент времени

0– ( iL (0− ) = iL (0+ ) и uC (0− ) = uC (0+ ) ).

233

Соотношение (4.48) легко программируется и имеет ясный физический смысл. Оно определяет положение точки в пространстве состояний на (n + 1)-м шаге, исходя из ее состояния на n-м шаге при аппроксимации траектории на участке ∆t прямолинейным отрезком с постоянной скоростью x&(∆t) .

Нахождение коэффициентов матриц связи А и В возможно путем записи полной системы уравнений Кирхгофа и преобразования их к совокупности n дифференциальных уравнений первого порядка в форме (4.45) относительно токов индуктивностей и напряжений на емкостях. Точно так же совокупность l алгебраических уравнений Кирхгофа, выражающих в форме (4.46) выходные величины, определяют коэффициенты матриц С и D. Чтобы каждое уравнение, записанное по первому и второму законам Кирхгофа, было дифференциальным уравнением первого порядка относительно iL и uC, каждый контур и сечение должны содержать только один реактивный элемент.

Однако возможно применение стандартной процедуры построения матриц связи, не требующих предварительного составления уравнений Кирхгофа. Основанием для этого служит то обстоятельство, что элементы матриц A, B, C, D являются псевдопередаточными коэффициентами вспомогательных резистивных цепей.

С целью нахождения коэффициентов матриц связи запишем для момента t = 0+ систему уравнений (4.45) в матричной форме (4.49).

234

Если в уравнении (4.49) попеременно полагать все начальные значения x1 (0), K, xn (0), v1 (0), K, vm (0) равными нулю, кроме одного, приравниваемого единице, значения элементов расширенной

ветствующего столбца матриц A и C либо B и D. Данное утверждение формирует алгоритм определения искомых матриц, основанный на принципе суперпозиции.

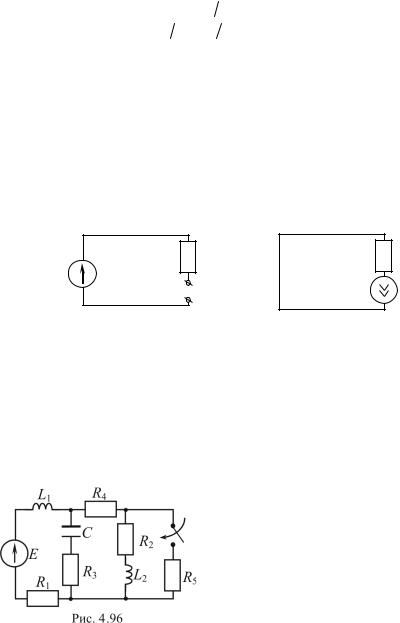
В исходной цепи выделяются источники воздействия (для определенности k), индуктивности (q) и емкости (m), затем образуется расчетная резистивная цепь, в которой удалены все источники воздействия (источники ЭДС замыкают накоротко, ветви с источниками тока размыкают), оборваны ветви, содержащие индуктивности, и замкнуты накоротко емкости.

Эта цепь рассчитывается по методу наложения. Сначала единичный источник тока включают поочередно q раз вместо каждой индуктивности, далее единичный источник напряжения включают поочередно m раз вместо каждой емкости. И, наконец, единичные источники напряжения и тока включаются поочередно k раз в ветви, где были расположены источники соответствующих воздействий vi. при расчете каждой из таких вспомогательных схем определяются значения напряжений uL , токов iC и выходных величин y,

которые удобно записывать в виде таблицы, содержащей искомые значения элементов матриц.

Пример. Проиллюстрируем предлагаемую методику на примере цепи второго порядка (см. рис. 4.23).

Матричная схема уравнений в переменных состояния для произвольной цепи имеет вид (4.45). В этой системе уравнений переменными состояния для электрической цепи (см. рис. 4.23) являются индуктивный ток iL и емкостное напряжение uC, входными функциями – напряжение источника ЭДС E и ток источника тока J, выходная

235

В соответствии с вышеизложенным матричная система уравнений принимает следующий вид:

Рассмотрим два способа получения матриц связи:

1. Получение коэффициентов матриц А, В, С, D с помощью составления системы уравнений Кирхгофа:

или в дифференциальной форме:

Произведя необходимые преобразования и подстановки, а также с учетом того, что i2 = iC , i3 = iL , получим

236

i1 = E −uC . R1

Выразим из полученной системы уравнений искомые коэффициенты матриц связи:

2. Получение коэффициентов матриц А, В, С, D с помощью канонической процедуры. В процессе решения заполняется табл. 4.2 по изложенным выше правилам.

Искомые коэффициенты определяются в результате рассмотрения вспомогательных резистивных цепей (рис. 4.89–4.92):

а) UJ =−uL = JR2 = R2 , uL′ = uL L ,

следовательно, iL′ = R2 L = a11 ; б) iC = J L = CuC′ , следовательно,

uC′ =1C = a21 ;

в) i1 = 0 , следовательно, с1 = 0.

237

a) uL = – EC = –1 , следовательно,

iL′ = –1/ L = b12;

б) iC= – EC/R1 = –1/ R1 , следовательно,

uC′ = –1/ R1C = b22;

в) uC = EC = 1, следовательно, i1 = – EC/R1 = –1/ R1 = с2 ;

a) i1 = E/R1 = 1/R1 = d1;

б) uL = 0, следовательно,

iL′ = 0 = b11;

в) iC = E/R1 = 1/R1, следовательно, b21 = uC′ = 1/R1C;

a) i1 = 0, следовательно, d2 = 0; б) iC = 0, следовательно,

uC′ = 0 = b22;

в) uL = JR2 = R2, следовательно, iL′ = R2/L и b12 = R2/L.

Как мы убедились, предлагаемая технология отличается наглядностью и сводится к привычному расчету цепей с источниками постоянных воздействий.

4.6.1. Задачи и вопросы

Типовые задачи

Задача 1.

Дано: для электрической цепи (рис. 4.93) заданы параметры ее элементов: E = 40 В, R = 40 Ом, С = 500 мкФ, L = 1 Гн.

238

откуда определяем:

Из этих уравнений получим значения первых производных переменных состояния:

или в матричной форме:

239

Это матричное уравнение необходимо еще дополнить матрицей начальных состояний цепи, которая включает напряжение на емкости и ток в индуктивности в момент времени t = 0− :

Коэффициенты матричного уравнения также можно получить методом наложения, рассмотрев две подсхемы с источниками единичных воздействий (рис. 4.95).

а Рис. 4.95 б

Задача 2.

Дано: для электрической цепи (рис. 4.96) заданы параметры

ее элементов: E = 120 В, R1 = R3 = R4 = 1 Ом, R2 = R5 = 2 Ом,

L1 = 1 мГн, L2 = 2 мГн, С = 10 мкФ.

Найти: уравнение состояния.

Решение. Представленная электрическая схема (см. рис. 4.96) третьего порядка. Получение уравнения состояния при помощи уравнений Кирхгофа представляет определенные сложности. Наиболее рационально при решении этой задачи воспользоваться методом наложения, рассчитав схему замещения (рис. 4.97), в которой реактивные элементы заменены единичными источниками ЭДСитока. Втакой схеме

240