
4601
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
Е.А. Мясников
МАТЕМАТИКА В ЭКОНОМИКЕ: ПРИМЕРЫ ПРИЛОЖЕНИЙ
Хабаровск 2013
УДК 51 (075.8)
ББК В Х 12
Математика в экономике: примеры приложений : метод. указания / сост. Е. А. Мясников. – Хабаровск : РИЦ ХГАЭП, 2013. – 32 с.
Содержание методических указаний соответствует государственным образовательным стандартам математических дисциплин для бакалаврантов 1-го курса обучения. Учтены разделы, входящие в программу общей математической подготовки. Даны примеры применения основных математических понятий в повседневных и исследовательских задачах экономики. Указания предназначены для самостоятельного изучения. Составлены для бакалаврантов экономических вузов всех направлений подготовки.
Рецензент Е. Г. Агапова, к.ф.-м.н., доцент каф. прикладной математики ТОГУ
Утверждено издательско-библиотечным советом академии
вкачестве методических указаний
©Мясников Е.А., 2013
©Хабаровская государственная академия экономики и права, 2013
2
Предисловие
Цель указаний – привести некоторые примеры применения математики в экономических дисциплинах и в управлении экономикой и финансами.
Качественное преподавание математики невозможно без рассказа об её практическом применении в будущей деятельности специалиста. Однако преподаватель с классическим образованием, не знакомый с особенностями экономики, для этого вынужден сам изучать специальную литературу, что требует немалого энтузиазма и времени. При дефиците аудиторных часов обзор приложений и вовсе невозможен, и преподавание ограничивается изложением общей теории и отвлечённых примеров.
По тем же причинам преподаватель специальных дисциплин не всегда видит математические стороны какой-либо проблемы и тем более не может отвести время на их обсуждение со студентами.
В результате студенты постоянно слышат о важности математики, но так и не узнают, в чём она. Усложнение задач экономики и управления требует развитых методов решения, но разрыв между математическим и специальным образованием (и производством) сводит все методы к интуиции руководителя или эксперта. Серьёзные же экономические журналы со сложными формулами, предлагающие объективное решение проблем, остаются для студентов в стороне.
Между тем современные экономические исследования по сложности применяемой математики уступают лишь немногим областям – в основном физике, метеорологии и военным разработкам. Операции, применяемые в работе рядового экономиста (и реализованные в компьютерных программах), проще, но некоторые методы, например, линейное программирование, возникли именно для решения обычных задач и лишь затем формировались в строгую теорию.
Математики не придумывают правила, как в спортивных играх, и не изобретают теоремы. Исходя из практических наблюдений, они подмечают закономерности в числовых и пространственных соотношениях в реальном мире и на их основе находят всё более сложные объективные зависимости – причём как можно в более простом виде.
Модели реального мира, в том числе модели экономики, высоко ценятся именно тогда, когда выражаются простыми формулами и уравнениями – это позволяет легко с ними работать и строить прогнозы. К сожалению, связи в современной экономике настолько сложны, что нередко приводят к моделям, допускающим лишь приближённое решение.
3
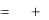
В указаниях кратко, по возможности без формул, рассказано, где применяются стандартные понятия математики – матрицы, интегралы и т.п. Обращено внимание на повседневные задачи и на известные модели экономики.
Дополнительно даны примеры сложных прикладных задач и указано, какие средства используются при их решении.
Задания для самостоятельной работы можно найти в [1]. Не включены темы прикладных дисциплин – методов оптимизации, эконометрики и др., практическая направленность которых для студентов очевидна.
Замечание об истории экономических исследований
Систематическое изучение экономики средствами математики начато в XVII веке – с развитием промышленной революции в Европе. Возникшие тогда же дифференциальное и интегральное исчисление позволили изучать непрерывные во времени процессы и проводить недоступные раньше вычисления.
Обзор развития математического моделирования экономики (ММЭ) можно найти, например в [2]. Там же изложены основные понятия и принципы ММЭ.
Важнейшие направления применения математики в экономике в наше время:
1)моделирование макроэкономики, микроэкономики, финансовых рынков и прогнозирование;
2)оптимизация управления сложными системами;
3)статистическая обработка развёрнутых структур информации.
Последнее направление популярно и в областях, ранее далёких от математики – в социологии, связях с общественностью, юриспруденции и т.п.
Фундаментальная (теоретическая) математика обеспечивает прикладные области новыми способами решения задач и обосновывает точность и адекватность этих способов, а также изучает границы их применения.
Линейная функция и кривые 2-го порядка
Линейная функция y kx b связана с простейшей задачей прогнозирования –
по известному значению показателя X выяснить наиболее вероятное значение величины Y. Даже если реальная зависимость сложнее, подвержена влиянию случайных факторов или является косвенной (обе величины зависят от 3-й), возможность считать одну величину линейно зависящей от другой высоко ценится в исследованиях и прогнозах.
4

Так, расходы на питание нелинейно (выпуклостью вверх) зависят от доходов семьи, но на небольшом участке и в одинаковых условиях, например, когда доходы близки к прожиточному минимуму, зависимость почти линейна. Издержки производства квадратично меняются при большом разбросе выпуска, но фактически линейны при его малом изменении.
На рисунке 1(а) приведён пример зависимости, близкой к линейной. По горизонтали отмечено число пропусков N для 13 студентов, по вертикали – процент выполнения работ в семестре (P). Зависимость с надёжностью 93% задаётся функцией P 85,76 3,084N , т.е. на 93% величина P объясняется числом пропусков N. Теоретические значения на рисунке 1(б) почти равны настоящим.
100 |
|
|
|
|
80 |
|
|
|
|
60 |
|
|
|
|
40 |
|
|
|
|
20 |
а) |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
5 |
10 |
15 |
20 |
100 |
|
|
|
|
90 |
|
|
|
|
80 |
|
|
|
|
70 |
|
|
|
|
60 |
|
|
|
|
50 |
|
|
|
|
40 |
|
|
|
|
30 |
|
|
|
|
20 |
б) |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
0 |
|
|
|
|
0 |
5 |
10 |
15 |
20 |
Рисунок 1 – Выполнение учебного графика в некоторой группе
При нелинейной зависимости также можно прогнозировать поведение одной величины по другой, но тогда сложнее найти параметры самой зависимости и доверительные границы для прогноза.
Поиск коэффициентов линейной функции основан на дифференцировании функции двух переменных и принципах математической статистики.
Если на величину Y действуют несколько факторов X1 , X 2 , , X m , зависи-
мость от них также стараются свести к линейной функции y b0 b1 x1 bm xm .
Например, прибыль может зависеть от расходов на рекламу, вложений в производство, численности сотрудников и т.п.
Линейная функция применяется в задачах линейного программирования. Так, затраты сырья и выручка обычно пропорциональны объёму выпущенных товаров. С ростом выпуска увеличатся и затраты, и выручка. Чтобы подобрать ассортимент выпуска, при котором выручка максимальна, а затраты не превышают доступных ресурсов, понадобятся свойства линейной функции.
5
Те же свойства покажут, запасы какого сырья стоит увеличить для существенного увеличения выручки, поможет ли экономия ресурсов, выгодно ли повышать цены на продукцию, и т.д.
Приближённые вычисления, численное решение дифференциальных уравнений и другие сложные действия связаны с переходом к линейной функции.
Тем не менее иногда нелинейность величины важна. Так, издержки Y большого производства квадратично растут при росте выпуска X: y a bx cx2 , и
слагаемым cx 2 нельзя пренебречь. Получается уравнение параболы. Если предприятие выпускает 2 вида продукции, получаются 2 функции издержек.
На рисунке 2 слева построены параболы – графики издержек производства на 2 предприятиях. В центре видны части эллипсов – линий уровня, где совместные издержки одинаковы. Справа даны фрагменты гипербол – линий, на которых издержки отличаются на одинаковую величину.
4500 |
|
|
|
|
|
|
4000 |
|
|
|
|
|
|
3500 |
|
|
|
|
|
|
3000 |
|
|
|
|
|
|
2500 |
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
1500 |
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
500 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
10 |
14 |
18 |
22 |
26 |
30 |
34 |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
28 |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
28 |
Рисунок 2 – Издержки предприятий и линии уровня для совместных издержек
Если искать совместные издержки работы нескольких (3 и более) предприятий, возникают квадратичные формы, геометрически задающие некие поверхности в многомерном пространстве – эллипсоиды и гиперболоиды. Работа с такими функциями (например, поиск минимума) сложна, и всегда стараются сгруппировать показатели, для чего применяют собственные числа и векторы.
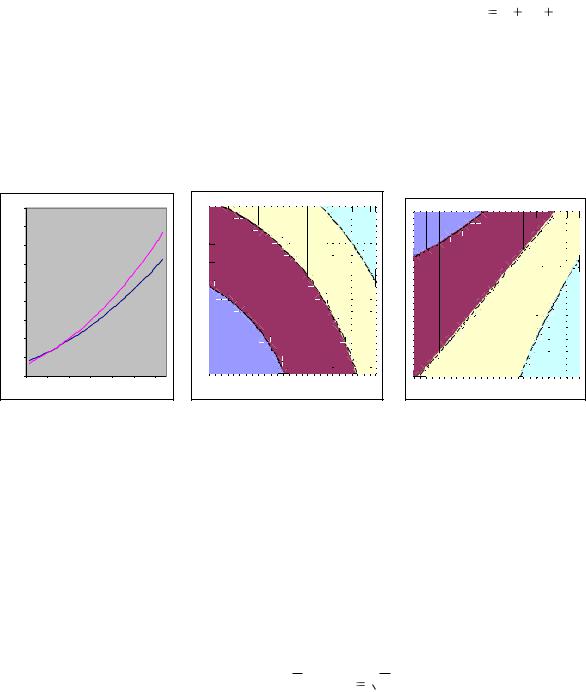
Кривые 2-го порядка появляются, если изучать зависимость выпуска продукции от вложенных средств или полезность некоторого товара или услуги. Выпуск растёт медленнее, чем инвестиции, а ценность товара – медленнее, чем его объём, и возникают функция типа y 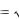
 x или y 3
x или y 3  x .
x .
Кривые безразличия (линии одинаковой полезности) в теории потребления и изокванты (линии равного выпуска) в теории фирмы обычно обладают свойствами гиперболы – выпуклы вниз и убывают (рисунок 3).
6
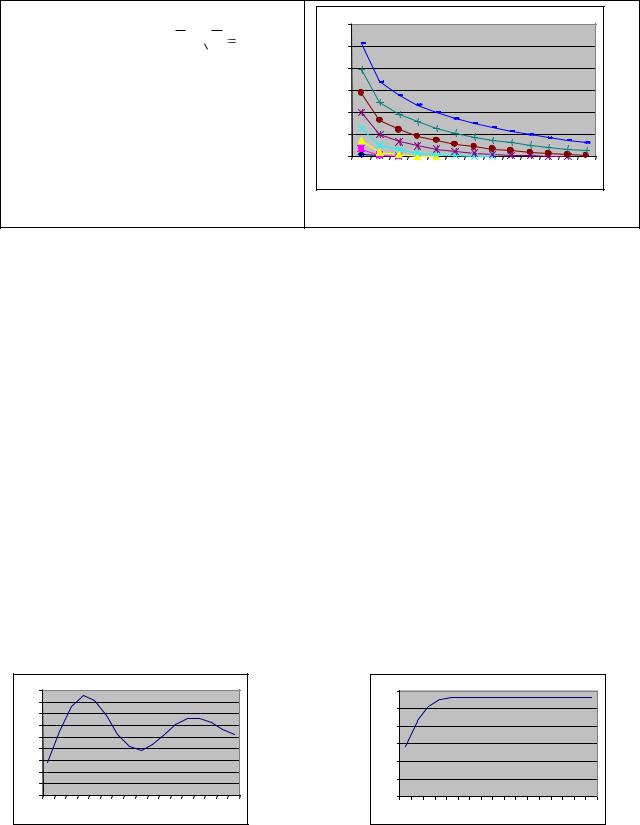
Справа построены кривые безразличия для функции 3
 x
x 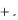
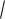 y C .
y C .
С ростом полезности С линии удаляются от начала координат.
На каждой отдельной кривой общая полезность товаров одинакова. По горизонтали указан объём 1-го товара, по вертикали – 2-го.
300 |
|
|
|
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 12 |
Рисунок 3 – Кривые безразличия |
|
||||||||||
Обратите внимание на резкий рост графиков при приближении к вертикальной оси: отсутствие 1-го товара трудно компенсировать приобретением 2-го.
Умение построить эллипс или гиперболу по уравнению помогает быстро решить графически задачу о максимальной выручке, когда аналитическое решение громоздко и мало эффективно.
Другие элементарные функции
Функции sin и cos нужны для изучения периодических и циклических процессов, при наличии сезонной составляющей в спросе на товар, занятости и т.д.
Инвестиции в моделях макроэкономики часто пропорциональны разности выпуска за 2 года: очевидно стремление вложить средства во что-то перспективное. Если такое стремление имеет место при малых запросах потребителей, выпуск ведёт себя как затухающая синусоида (рисунок 4, а). При слабой реакции на изменение выпуска (или при большом спросе) выпуск превращается в сумму показательных функций и стремится к постоянной величине (рисунок 4, б).
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
120 |
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 11 12 13 14 |
15 16 |
17 |
а) высокая склонность к инвестициям; б) низкая склонность к инвестициям
Рисунок 4 – Выпуск продукции в модели Самюэльсона – Хикса
7
Функция tg больше связана с эластичностью величин с сезонными составляющими, когда выясняют, например, процент изменения занятости при изменении нормы потребления на 1% (или наоборот).
Во многих процессах скорость изменения величины пропорциональна самой величине. Это рост населения (рисунок 5), рост экономики при инвестициях, зависящих от выпуска (модель Харрода, [6]), распространение информации и т.п. Здесь важна показательная функция e x .
1,4 |
|
1,3 |
2 |
1,2 |
|
1,1 |
1 |
|
|
1 |
|
Рисунок 5 – Рост населения за 10 лет при темпах прироста 1,5% (1) и 3% (2)
Множитель e x учитывает обесценивание денег (рисунок 6), старение оборудования или важность немедленного дохода по сравнению с перспективным.
1 |
|
|
|
|
|
|
1 |
|
|
0,8 |
|
|
|
|
|
|
2 |
|
|
0,6 |
|
|
|
|
0,4 |
|
|
|
|
0 |
8 |
16 |
24 |
32 |
Рисунок 6 – обесценивание денег за 3 года при инфляции 10% (1) и 30% (2) в год
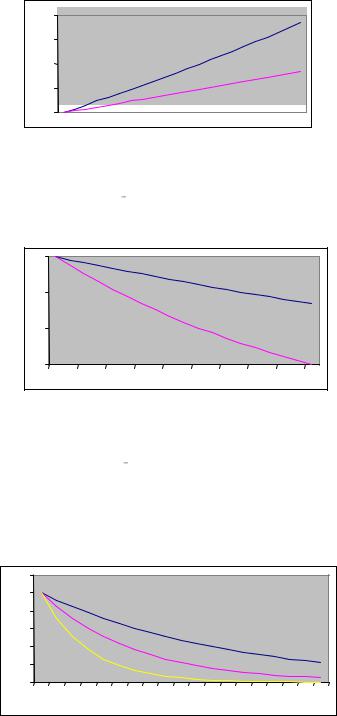
С функцией e x связаны время работы сотрудника до болезни и время работы бытовой техники до поломки. На рисунке 7 отражена ситуация, когда 1-й сотрудник болеет в среднем 2 раза в год, 2-й – 1 раз в год, 3-й – раз в 2 года. По горизонтали – число месяцев.
1,2 |
|
|
|
|
|
1 |
|
|
|
|
|
0,8 |
|
|
3 |
|
|
0,6 |
|
|
|
|
|
0,4 |
|
|
|
|
2 |
0,2 |
|
|
1 |
|
|
0 |
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 12 14 16 18 20 22 24 26 28 30 32 34 |
Рисунок 7 – Шансы проработать без больничного листа для 3 сотрудников
8
Очевидно, что при решении указанных задач появляются и обратные тригонометрические функции типа arctg или логарифмическая функция ln. Логарифмическая функция нужна для моделирования распространения информации (в том числе рекламы), эпидемий и деятельности финансовых пирамид.
Функции нескольких переменных
Функции нескольких переменных появляются, когда интересующий нас показатель зависит от разных факторов. Таковы, например, функции полезности и производственные функции (ПФ).
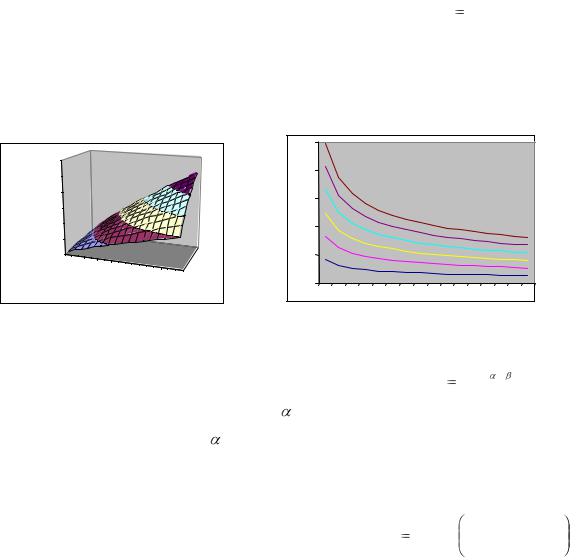
В 1960 – 95 гг. выпуск ВВП США (в млрд долл.) составлял Y 2,248K 0,404L0,803 , где K – фонды, млрд долл., L – трудовые ресурсы, млн чел. [4]. Таким образом, объём выпуска – функция от имеющихся фондов (капитала) и затрат труда. На рисунке 8(а) построен её график в виде поверхности, а на рисунке 8(б) – в виде изоквант (линий одинакового выпуска ВВП) c шагом 2 трлн долл.
|
|
|
|
|
|
2000 |
|
|
|
|
ВВП 12000 |
|
|
|
|
|
Y=12 000 |
|
|
|
|
10000 |
|
|
|
|
|
1600 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8000 |
|
|
|
|
|
1200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6000 |
|
|
|
|
|
|
|
|
|
|
4000 |
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
400 |
|
|
|
|
20 |
80 |
140 |
200 |
260 |
320 |
0 |
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
100 |
180 |
260 |
. |
|
|
|
|
|
|
|
|
|
|
|
Рисунок 8 – Выпуск ВВП США
Выпуск ВВП обычно задаётся функцией Кобба – Дугласа Y A0 K L , где K –
фонды производства, L – затраты труда, , 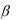 – эластичность по фондам и труду соответственно. Параметры A0 , ,
– эластичность по фондам и труду соответственно. Параметры A0 , , 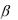 различны для разных стран и секторов эко-
различны для разных стран и секторов эко-
номики. От соотношения параметров зависит оптимальное распределение ресурсов по секторам (когда ищется максимум среднедушевого потребления).
Выпуск в микроэкономике часто задан функцией |
Y A min |
X |
; |
Y |
; ; |
Z |
, |
|
|
|
|||||
|
0 |
X 0 |
Y0 |
|
Z0 |
|
|
|
|
|
|
||||
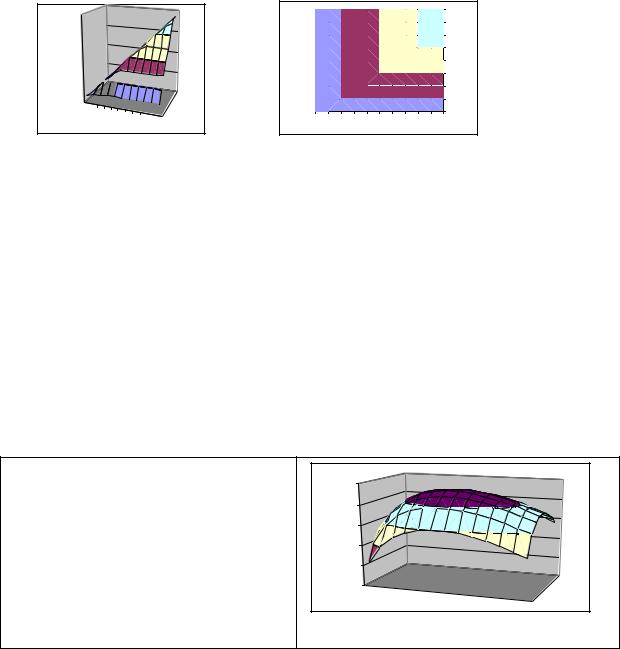
где X ,Y , , Z – запасы сырья, а X 0 ,Y0 , , Z0 – нормы расхода сырья на 1 ед. про-
дукции. Такая зависимость (функция Леонтьева) имеет место, если ресурсы не заменяют друг друга (как доски, ткань, краска и гвозди). График и изокванты функции Леонтьева приведены на рисунке 9.
9
4 
3 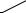
2 
1 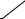





0 





 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 


|
|
|
|
|
|
|
|
|
|
Р9 |
|
|
|
|
|
|
|
|
|
|
Р8 |
|
|
|
|
|
|
|
|
|
|
Р7 |
|
|
|
|
|
|
|
|
|
|
Р6 |
|
|
|
|
|
|
|
|
|
|
Р5 |
|
|
|
|
|
|
|
|
|
|
Р4 |
|
|
|
|
|
|
|
|
|
|
Р3 |
|
|
|
|
|
|
|
|
|
|
Р2 |
|
|
|
|
|
|
|
|
|
|
Р1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Рисунок 9 – Типичная функция Леонтьева
Для ПФ находят такие показатели, как средняя и предельная эффективность капитала и труда, фондоёмкость и трудоёмкость, эластичность по ресурсам, удельный выпуск, темпы прироста выпуска, нормы замещения труда капиталом (и наоборот), эластичность замещения. Слово «предельный» в названии показателя означает, что от показателя берётся производная по времени или некоторому фактору (ресурсу).
В известной задаче об оптимальном выпуске с увеличением выпуска продукции растёт выручка предприятия, но это требует всё новых закупок ресурса и увеличения выплат сотрудникам. С некоторого момента затраты растут быстрее выручки и прибыль падает (рисунок 10).
Справа |
показана |
зависимость |
|
|
|
|
550 |
прибыли от затрат капитала и труда. |
|
||
|
|
|
500 |
Вершина соответствует |
максимуму |
450 |
|
прибыли. |
Оптимальные затраты |
400 |
|
находят, дифференцируя функцию 2 |
350 |
||
|
|
|
300 |
переменных. |
|
|
|
|
|
|
Рисунок 10 – Изменение прибыли |
Матрицы и системы линейных уравнений
Матрицы позволяют компактно хранить большие объёмы информации, когда несколько объектов характеризуются одинаковыми признаками. Это могут быть оценки за сессию в группе, затраты сырья для разных товаров, сведения о продуктах питания и т.д. Когда над значениями признаков выполняют одни и те же действия, удобно сразу работать со всей матрицей.
Кроме того, матрицы незаменимы при решении больших систем линейных алгебраических уравнений и задач линейного программирования.
10
