
- •Введение
- •1. Основные понятия и утверждения о функциональных рядах
- •2. Упражнения и вопросы для самопроверки
- •3. Степенные ряды
- •4. Упражнения и вопросы для самопроверки
- •5. Ряды Тейлора и Маклорена
- •6. Упражнения и вопросы для самоконтроля
- •7. Применение степенных рядов в приближённых вычислениях
- •8. Упражнения и вопросы для самопроверки
- •9. Ряды Фурье
- •10. Упражнения и вопросы для самопроверки
- •Библиографический список
- •Содержание

что функция y e2x удовлетворяет дифференциальному уравнению (60) и
начальным условиям (61). |
|
|
|
|
|
|
|
|
|
|
||||
|
В заключение заметим, что с помощью разложений в степенные ря- |
|||||||||||||
ды можно вычислять пределы. |
|
|
|
|
|
|
|
|
|
|||||
|
Пример 42. Вычислим с помощью разложения в ряд Маклорена |
|||||||||||||
функции sin x первый замечательный предел |
lim |
sin x |
(разложение функ- |
|||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 0 |
x |
||
ции |
sin x |
приведено в примере 39). Получим, что |
|
|
||||||||||
|
|
|
||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
sin x |
|
lim |
1 |
x2 |
|
x4 |
|
x6 |
|
1. |
|
|
|
x |
3! |
5! |
|
7! |
|
|||||||
|
|
x 0 |
x 0 |
|
|
|
|
|
||||||
8.Упражнения и вопросы для самопроверки
1.Пользуясь соответствующим рядом, вычислить указанное значе-
ние функции с заданной точностью |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1.1) |
e |
0,2 |
|
, |
|
|
|
0,0001; |
1.2) |
e |
0,1 |
, |
|
|
|
|
|
|
0,000 01; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.3) |
|
|
|
|
|
|
|
|
, |
|
0,0001; |
1.4) |
|
|
|
|
|
|
, |
|
|
|
0,000 01; |
||||
sin 18 |
|
|
cos5 |
|
|
|
|
||||||||||||||||||||
1.5) |
cos |
|
|
|
|
, |
|
0,000 01 |
1.6) |
sin 10 , |
|
|
|
0,0001; |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.7) |
ln 3, |
|
|
|
|
0,0001; |
1.8) |
ln 5, |
|
|
|
|
|
0,001; |
|||||||||||||
1.9) |
3 |
|
|
, |
|
|
|
|
|
0,001; |
1.10) 3 |
|
|
|
, |
|
|
|
0,001; |
||||||||
9 |
|
|
|
|
|
30 |
|
|
|
||||||||||||||||||
1.11) arctg |
1 |
, |
0,000 002 ; |
1.12) arcsin |
|
1 |
, |
0,000 001. |
|||||||||||||||||||
10 |
10 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. Найти с какой-нибудь точностью следующие значения: |
|||||||||||||||||||||||||||
2.1) |
sin 5 , |
|
|
|
2.2) |
cos |
|
|
|
|
, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|||||||
2.3) |
5 |
|
, |
|
|
|
|
2.4) |
4 |
|
. |
|
|
|
|
|
|
|
|||||||||
35 |
|
|
|
|
17 |
|
|
|
|
|
|
|
|||||||||||||||
81

3. Вычислить определённые интегралы с точностью до  0,001:
0,001:
|
1 |
x 2 dx , |
|
1 |
|
|
|
|
|
3.1) |
e |
3.2) |
cos xdx , |
|
|||||
|
0 |
|
|
|
0 |
|
|
|
|
3.3) |
12 arctgx |
dx , |
3.4) |
110 ln 1 x |
dx . |
||||
0 |
x |
0 |
|
x |
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
4. Вычислить приближённое значение интегралов, ограничившись двумя или тремя членами в разложении подынтегральной функции в ряд, и оценить получившуюся при этом погрешность:
|
1 |
|
|
|
|
|
|
|
|
0,5 |
|
|
|
2 |
|
|
|
|
|
|
|
sin x |
|
||
4.1) |
e |
|
|
x |
dx , |
4.2) |
|
dx , |
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
|||||
|
0 |
|
|
|
|
|
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
|
4.3) |
|
4 x |
|
dx , |
|
4 sin x2 dx , |
||||||
e |
|
|
4.4) |
|||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
4.5) |
1 |
arctgx |
dx , |
4.6) |
1sin x2 dx . |
|||||||
|
||||||||||||
|
0 |
|
|
x |
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
5. Найти решения задач Коши для заданных дифференциальных уравнений при указанных начальных условиях:
5.1) |
y |
|
|
|
2xy |
|
|
1 |
y |
ex 2x2 |
3x |
3 , |
y 0 |
|
|
0 , |
y 0 |
|
1; |
||||||
|
|
|
x |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.2) |
y |
|
|
|
xy |
|
y |
x cos x , |
y 0 |
0 , |
y |
0 |
1; |
|
|
|
|
|
|
|
|
||||
5.3) |
y |
|
|
|
xy |
|
x |
1 cos x , |
y 0 |
1, |
y |
0 |
0 ; |
|
|
|
|
|
|
|
|
||||
5.4) |
y |
|
xy |
|
e y , |
y 0 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6. Разложив соответствующие функции в ряд, вычислить следующие |
|||||||||||||||||||||||||
пределы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.1) |
lim |
1 |
|
cos x |
, |
|
|
|
6.2) |
lim |
ln 1 |
x |
, |
||||||||||||
|
|
x2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
x |
|
|
|
||||
|
|
|
|
|
e |
x |
|
1 |
|
|
|
|
|
|
6.4) |
lim |
1 |
cos x |
|
, |
|||||
6.3) |
lim |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
x |
0 x e x |
1 |
|
|
||||||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
82

|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
x |
sin x |
|
|
|
||||
6.5) |
lim |
1 |
|
x 1 |
, |
6.6) |
lim |
|
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
0 |
|
|
|
|
|
x |
|
x |
0 |
|
|
x3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
x |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
x |
|
6.8) |
lim |
, |
|
||||||||||||
6.7) |
lim |
|
|
, |
|
|
x |
|
|
||||||||||||||
|
|
|
|
|
x |
x |
0 |
|
|
|
|
|
|
||||||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
e |
x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|||
6.9) |
lim |
|
|
, |
|
|
|
|
|
6.10) |
|
lim |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x2 |
sin 2 x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
0 x3 |
|
|
|
|
|
|
|
|
x |
0 |
|
||||||||||
7.Какие приложения степенных рядов рассмотрены в этом пункте?
8.Как оценивается погрешноть при приближённых вычислениях значений функции с помощью их разложения в степенные ряды?
9.Каким образом можно оценить погрешность приближённого значения данной функции в некоторой точке, если получился числовой ряд Лейбница?
10.Можно ли оценить погрешность приближения функции некоторой частичной суммой соответствующего ряда по остаточному члену формулы Тейлора этой функции?
11.Какой вид имеет остаточный член формулы Маклорена в форме Лагранжа?
12.Каким равенством связана абсолютная погрешность приближения функции частичной суммой ряда Маклорена этой функции с остаточным членом её формулы Маклорена?
13.Как можно оценить погрешность приближения функции ex в некоторой точке частичной сумой её ряда Маклорена?
14.При приближённом вычислении значения функции в данной точке с помощью ряда получился положительный числовой ряд. Как можно оценить погрешность приближения по остатку этого ряда?
15.Для остатка приближения функции в точке найден мажорирующий ряд и вычислена его сумма. Что можно сказать о точности приближения значения функции соответствующей частичной суммой этого ряда?
16.Каким образом можно приближённо вычислять определённые интегралы?
17.От каких функций интегралы не выражаются в конечном виде через элементарные функции?
83

18. Можно ли вычислить определённый интеграл по отрезку 0,1 от функции e x 2 с помощью формулы Ньютона – Лейбница?
от функции e x 2 с помощью формулы Ньютона – Лейбница?
19.Какой интеграл называется интегралом вероятностей? Как вычисляются значения этого интеграла при конкретных значениях x ?
20.Какие величины нужно найти, если функция, являющаяся решением дифференциального уравнения, ищется в виде степенного ряда?
21.В чём состоит метод неопределённых коэффициентов для решения дифференциального уравнения?
22.Для каких дифференциальных уравнений наиболее удобен метод неопределённых коэффициентов?
23.В виде какого ряда нужно искать решение линейного дифференциального уравнения первого порядка, если начальное условие задаётся в
точке x 0 x x0 ?
24. В виде какого ряда удобнее искать решение линейного дифференциального уравнения второго порядка, если начальные условия задаются в точке x 0 x x0 ?
25. |
Можно ли вычислять предел функции в точке с помощью ряда, |
|||
который не сходится к значению функции в этой точке? |
||||
26. |
Можно ли найти предел |
lim |
arctgx |
с помощью разложения |
|
||||
|
x |
|
x |
|
arctgx в степенной ряд?
9.Ряды Фурье
Впараграфах 3, 5, 7 установлено, какую большую роль играют степенные ряды. Слагаемые ряда по степеням переменной x выражаются с помощью коэффициентов через систему
1, x, x2 , x3, ... , xn , ...
степенных функций, которые являются весьма простыми. Поэтому представления функций в виде степенных рядов дают возможность вычислить приближённые значения таких функций с любой степенью точности и находить пределы. Так как степенные ряды можно дифференцировать и
84

интегрировать в области их сходимости, то они находят приложения к решению дифференциальных уравнений и вычислению определённых интегралов. Такое же значение имеют и более общие степенные ряды – ряды по степеням двучлена x x0 .
Чтобы функция разлагалась в степенной ряд, необходима её бесконечная дифференцируемость. Например, достаточно простую функцию y x нельзя разложить по степеням x , так как она недифференцируема в точке x 0. Поэтому представляет интерес способ выражения функции ка- ким-нибудь другим функциональным рядом, кроме степенного.
В математике хорошо изучена система тригонометрических
функций |
|
1, cos x , sin x , cos 2x , sin 2x , …, cosnx, sin nx , … . |
(63) |
Далее будет обсуждаться вопрос о представлении функции в форме ряда по функциям этой системы.
Определение 14. Функциональные ряды видов
|
|
a0 |
|
an cos nx |
bn sin nx , |
(64) |
|||||||||
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a0 |
|
|
|
|
an cos |
|
n |
x |
bn sin |
n |
x , |
(65) |
||
2 |
|
|
|
n |
1 |
l |
l |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где l 0, a0 , an , bn |
n |
1, 2, ... – |
действительные |
числа, называются |
|||||||||||
тригонометрическими рядами. |
|
|
|
|
|
|
|||||||||
Числа a0 , an , bn |
называются коэффициентами тригонометриче- |
||||||||||||||
ского ряда. Обозначение |
a0 |
свободного члена выбрано для удобства и |
|||||||||||||
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
станет понятно из дальнейших выкладок.
Ряд (64) является частным случаем ряда (65); он получается из него при l  .
.
Изучение ряда (65) сводится с помощью замены переменной t |
|
x |
l |
к изучению ряда (64) относительно переменной t . Отсюда следует, что ес-
85

ли X – область сходимости ряда (64), то множество x : l x X есть об-
ласть сходимости ряда (65).
Итак, приступим к изучению тригонометрического ряда (64).
Прежде всего отметим, что если ряд (64) сходится, то его сумма S x есть периодическая функция с периодом 2 , так как все функции системы
есть периодическая функция с периодом 2 , так как все функции системы
(63) являются периодическими функциями с периодом 2 |
. Действительно, |
||||||||
при n |
1, 2, ... |
|
sin nx и cosnx имеют период, равный |
2 |
. Следовательно, |
||||
|
n |
||||||||
|
|
|
|
|
|
|
|
|
|
число |
n |
2 |
|
также является их периодом; постоянное же число |
a0 |
||||
|
|
|
2 |
|
|||||
|
|
|
n |
|
|
|
|||
можно считать периодической функцией с каким угодно периодом и, в частности, с периодом 2 .
Напомним, что функция |
f |
x |
называется периодической, если су- |
ществует такое число T 0 , что в каждой точке области определения этой |
|||
функции имеет место равенство |
|
|
|
f |
x |
T |
f x . |
При этом число T называют периодом этой функции. Коротко говорят, что функция f x T – периодична.
T – периодична.
Из сказанного в предыдущем абзаце следует, что тригонометрические ряды вида (64) являются очень удобным аппаратом для представления через них 2 – периодических функций.
Замечание 29. Ряд (64) можно записать в виде
|
a0 |
An sin |
nx |
n . |
|
|
|
|
|
(66) |
||||
|
2 |
|
|
|
|
|
|
|||||||
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для этого надо положить |
a |
n |
A sin |
n |
, b |
A cos |
n |
A |
a2 |
b2 |
|
и |
||
|
|
n |
n |
n |
|
n |
n |
n |
|
|
||||
воспользоваться тригонометрической формулой |
|
|
|
|
|
|
|
|||||||
sin |
|
|
|
sin |
cos |
|
cos |
sin . |
|
|
|
|
|
|
86

Функции вида y Asin |
x |
, имеющие период T |
2 |
, называют |
|
||||
|
гармониками, а разложения функций в ряды (66) называют разложениями в ряды по гармоническим колебаниям.
Систему (63) тригонометрических функций будем теперь рассматривать на отрезке  , , на котором все её функции являются 2 – периодичными. На этом отрезке она обладает очень важным свойством, называ-
, , на котором все её функции являются 2 – периодичными. На этом отрезке она обладает очень важным свойством, называ-
емым ортогональностью системы.
Определение 15. Система функций n x |
n 1, 2, ... , |
заданных на |
|
отрезке a, b , называется ортогональной системой на a, b , если |
|||
b |
|
|
|
n x m x dx 0 при n |
m , |
(67) |
|
a |
|
|
|
b |
|
|
|
n2 x dx |
0 при любом n . |
(68) |
|
a |
|
|
|
Второе условие (68) этого определения означает, что ни одна из |
|||
функций системы не может быть тождественным нулём. |
|
||
Теорема 17. Система (63) тригонометрических функций является ор- |
|||
тогональной системой на отрезке |
, . |
|
|
Доказательство. Проверим сначала выполнение условия (67) для системы (63). Для этого непосредственно с помощью формулы Ньютона – Лейбница надо вычислить интегралы: от произведения любого синуса и любого косинуса из системы (63) на единицу, от произведения двух косинусов с различными аргументами, от произведения двух синусов с разными аргументами, от произведения синуса на косинус с любыми n и m .
Выполним эти вычисления.
1. |
1 sin nxdx |
|
cos nx |
|
|
cos n |
|
cos n |
|
0 (в силу чёт- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n |
|
|
|
n |
|
|
n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
ности косинуса cos n |
cos n |
). |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
1 cos nxdx |
sin nx |
|
sin n |
|
|
sin |
n |
0 |
, так как sin n |
0 . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
n |
|
|
|
n |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. При n m:
87

cos mxcos nxdx |
1 |
cos m n xdx |
1 |
cos m n xdx |
1 |
0 |
1 |
0 0 |
|
2 |
2 |
2 |
2 |
||||||
|
|
|
|
|
(при этом была применена известная формула из тригонометрии и преды-
дущее вычисление 2, так как m |
n и m |
n есть целые числа, отличные от |
||||||||||||||||
нуля). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. При n m: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin mxsin nxdx |
1 |
cos m |
n xdx |
|
1 |
|
cos m n xdx |
1 |
0 |
|
1 |
|
0 0 |
|||||
2 |
2 |
|
2 |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(снова в силу известной формулы тригонометрии и вычисления 2). |
|
|||||||||||||||||
5. sin mxcos nxdx |
1 |
|
sin |
m |
n xdx |
1 |
sin m n xdx |
0 . |
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
2 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поясним это последнее вычисление. Первый интеграл справа в последней записи равен нулю в силу вычисления 1. Второй интеграл справа при n m равен нулю снова в силу вычисления 1; при n m этот интеграл равен нулю, так как подынтегральная функция есть тождественный нуль: sin m n x sin 0 0 .
Покажем, что система (63) удовлетворяет и условию (68) определения 15.
Как вычисляются интегралы от квадратов функций системы (63) по-
кажем в следующих выкладках: |
|
|
|
|
|
|
|
|
|
|
||||||||
6. |
|
|
|
|
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 dx x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. |
cos2 nxdx |
1 |
cos 2nx |
dx |
|
x |
|
|
sin 2nx |
|
|
|||||||
|
|
|
|
|
0 ; |
|||||||||||||
|
|
|
2 |
|
|
2 |
|
|
4n |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8. |
sin 2 nxdx |
1 |
cos 2nx |
dx |
x |
|
sin 2nx |
|
|
|
||||||||
|
|
|||||||||||||||||
|
|
0 . |
||||||||||||||||
|
|
|
2 |
2 |
|
|
|
4n |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, теорема полностью доказана.
При изучении разложения функций в степенной ряд было установлено следующее: если функция разлагается в степенной ряд, то это разложе-
88

ние единственно, а его коэффициенты вычисляются по определённым формулам (см. параграф 5; например, замечание 27). При этом степенной ряд есть её ряд Тейлора.
Попытаемся пойти по этому пути в случае тригонометрических
рядов. |
|
Итак, пусть некоторая функция f x определена на отрезке |
, |
(может быть, даже на всей числовой оси) и интегрируема на этом отрезке.
Пусть для всех x из |
, |
справедливо равенство |
|
||
f |
x |
a0 |
an cos nx bn sin nx . |
(69) |
|
2 |
|||||
|
|
n 1 |
|
||
|
|
|
|
||
Тогда говорят, что функция разлагается на |
, в тригонометрический |
|
ряд вида (64). |
|
|
Теорема 18. Если функция f x интегрируема на отрезке |
, и |
|
тригонометрический ряд (69) мажорируем на этом отрезке, то разложение (69) единственно, причём коэффициенты определяются равенствами
1 |
1 |
|
1 |
|
||
a0 |
|
f x dx , an |
|
f x cos nxdx, bn |
|
f x sin nxdx . (70) |
|
|
|
||||
Доказательство. Согласно параграфу 1 данного пособия, мажорируемые ряды можно почленно интегрировать. Тогда по условию теоремы ряд (69) можно интегрировать. Если ряд (69) умножим на cosmx или sin mx, то
в силу ограниченности этих функций ( |
cosmx |
|
1, |
sin mx |
1) новые ряды |
|
будут мажорируемыми и, следовательно, почленно интегрируемыми. |
|
|||||
Теперь приступим к установлению формул (70). |
|
|||||
Так как по условию теоремы функция f x |
интегрируема на |
, |
||||
и согласно отмеченному выше тригонометрический ряд (69) интегрируем,
то проинтегрируем обе части равенства (69) в пределах от |
до |
. В |
||||||||
результате получим следующее: |
|
|
|
|
|
|
||||
f x dx |
1 |
a |
|
1 dx |
a |
|
cos nxdx |
b sin nxdx . |
|
|
2 |
0 |
n |
|
|||||||
|
|
n |
1 |
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
||
Остаётся обратиться к теореме 17. Все участвующие в последнем равенстве интегралы вычислены при доказательстве этой теоремы (см. вычисле-
89

ния 1,2 и 6). Следовательно, |
f x dx |
1 |
a0 2 |
a0 , откуда получается |
|
2 |
|||||
|
|
|
|
первое из равенств (70).
Для получения второго равенства из (70) умножим (69) на cosmx,
после чего новое равенство проинтегрируем по отрезку |
, . В резуль- |
|||
тате получим: |
|
|
|
|
f x cos mxdx |
a0 |
cos mxdx |
|
|
2 |
|
|
||
|
|
|
|
|
an cos nx cos mxdx bn |
sin nx cos mxdx . |
|||
n 1 |
|
|
|
|
Интегралы, стоящие справа в этом равенстве, найдены при доказательстве теоремы 17 (см. вычисления 2, 3, 5 и 7). Все они равны нулю, кроме интеграла с коэффициентом am , который равен  (см. вычисление 7). Следовательно,
(см. вычисление 7). Следовательно,
f x cos mxdx am cos2 mxdx am ,
откуда получаем второе равенство из (70).
Таким же образом, умножая обе части равенства (69) на sin mx и интегрируя новое равенство почленно, получим третью из формул (70). При этом надо будет воспользоваться вычислениями 1, 4, 5 и 8 теоремы 17.
Замечание 30. Справедлива более общая теорема, чем теорема 18. В теореме 18 можно заменить мажорируемость ряда (69) на его равномерную
сходимость на отрезке |
, . |
|
|
|
|
|
Замечание 31. Из формул (70) становится понятным, почему сво- |
||||||
бодный член ряда (64) обозначен |
a0 |
(тогда все коэффициенты этого ряда |
||||
2 |
||||||
|
|
|
|
|
||
имеют перед интегралами один и тот же множитель |
1 |
). Кроме того, учи- |
||||
|
||||||
тывая что cosnx 1 при n |
0 , все коэффициенты an |
можно выразить еди- |
||||
ной формулой |
|
|
|
|
|
|
90

an |
1 |
f x cos nxdx |
n 0,1, 2, ... . |
|
Определение 16. Числа a0 , an , bn , вычисленные по формулам (70),
называются коэффициентами Фурье функции f x , а тригонометрический ряд (64), коэффициентами которого являются эти числа называется
тригонометрическим рядом Фурье этой функции.
В дальнейшем будем говорить «просто» ряд Фурье, а слово «тригономерический» будем опускать. Однако следует помнить, что могут быть ряды Фурье и по другим системам ортогональных функций n x , а не только по тригонометрической системе (63).
|
Обычно для ряда Фурье, составленного для интегрируемой на отрез- |
ке |
, функции f x , применяется обозначение |
f x ~ |
a0 |
|
a |
n |
cos nx |
b sin nx , |
|
|
|||||
2 |
|
|
|
n |
||
n |
1 |
|
|
|
||
|
|
|
|
|
||
при этом независимо от того, имеет ли этот ряд своей суммой функцию f x или нет.
или нет.
Замечание 32. В связи с определением 16 теорему 18 можно формулировать иначе: если интегрируемая на отрезке  ,
,  функция f x
функция f x разлагается в мажорируемый (в более общем случае – равномерно сходящийся) на этом отрезке тригонометрический ряд, то этот ряд является её рядом Фурье.
разлагается в мажорируемый (в более общем случае – равномерно сходящийся) на этом отрезке тригонометрический ряд, то этот ряд является её рядом Фурье.
Напомним теперь следующее. Когда функция f x является интегрируемой на отрезке и, следовательно, все интегралы (70) существуют, тогда можно будет говорить о ряде Фурье этой функции и его сходимости. Как известно, всякая непрерывная на любом отрезке функция является интегрируемой на этом отрезке. Интегрируемой является и любая ограничен-
является интегрируемой на отрезке и, следовательно, все интегралы (70) существуют, тогда можно будет говорить о ряде Фурье этой функции и его сходимости. Как известно, всякая непрерывная на любом отрезке функция является интегрируемой на этом отрезке. Интегрируемой является и любая ограничен-
ная на отрезке a, b |
функция с конечным числом точек разрыва первого |
|
рода на нём. |
|
|
К разрывам первого рода относят разрывы в тех точках x0 |
, в кото- |
|
рых односторонний |
пределы f x0 0 и f x0 0 конечны, |
но либо |
91

f x0 |
0 |
f x0 |
0 , либо |
f x0 |
0 |
f x0 |
0 |
|
f x0 . При этом предпо- |
||||
лагается, что в точке x0 |
функция определена. |
|
|
|
|||||||||
Односторонние пределы (левосторонний и правосторонний) функ- |
|||||||||||||
ции f |
x |
в точке x0 |
определяются равенствами |
|
|
||||||||
|
|
|
|
|
|
f |
x0 |
0 |
lim |
f |
x |
, |
|
|
|
|
|
|
|
|
|
x |
x0 |
0 |
|
|
|
|
|
|
|
|
|
f |
x0 |
0 |
lim |
f |
x . |
|
|
|
|
|
|
|
|
|
|
x |
x0 |
0 |
|
|
|
Запись x |
x0 |
0 означает, что x стремится к x0 , оставаясь слева |
x x0 . |
||||||||||
Запись |
x |
x0 |
0 |
означает, |
что |
x стремится к |
x0 только справа, |
всегда |
|||||
оставаясь больше x0 |
x |
x0 . |
|
|
|
|
|
|
|||||
Теорема 18 (см. также замечание 32) не означает, что всякая инте- |
|||||||||||||
грируемая (и даже непрерывная) на отрезке |
|
, функция на самом деле |
|||||||||||
разлагается в ряд Фурье. Например, совсем простая непрерывная функция
y x , рассматриваемая на отрезке |
|
, , не разлагается на всём отрезке |
|||||
в ряд Фурье. Действительно, у этой функции f |
f |
, |
а сумма три- |
||||
гонометрического ряда (64) в точках x |
и x |
должна иметь одина- |
|||||
ковые значения, так как она является |
2 – периодичной (это отмечено в |
||||||
самом начале параграфа). |
|
|
|
|
|
|
|
Таким образом, нужно ответить на следующие вопросы: |
|
|
|
||||
1) о сходимости ряда Фурье, порождённого функцией |
f |
x |
с кон- |
||||
кретными свойствами, на отрезке |
, |
; |
|
|
|
|
|
2) о том, когда сумма ряда Фурье сходится к функции |
f |
x |
, по ко- |
||||
торой этот ряд составлен.
Приведём далее две теоремы, дающие достаточные условия представимости функции f x её рядом Фурье. Доказательства этих теорем выходят за рамки данного учебного пособия. Они требуют достаточно сложных рассуждений и более глубоких знаний математического анализа.
её рядом Фурье. Доказательства этих теорем выходят за рамки данного учебного пособия. Они требуют достаточно сложных рассуждений и более глубоких знаний математического анализа.
Теорема 19. Пусть функция f x определена на отрезке
определена на отрезке  ,
,  и в каждой его точке имеет конечную производную f
и в каждой его точке имеет конечную производную f  x . Тогда ряд Фурье, порождённый этой функцией, сходится на этом отрезке, причём его сумма S x
x . Тогда ряд Фурье, порождённый этой функцией, сходится на этом отрезке, причём его сумма S x равна f x
равна f x в точках x интервала
в точках x интервала  ,
,  , а на концах промежутка
, а на концах промежутка
92

S |
f |
|
f |
. |
(71) |
|
|
|
|||
|
2 |
|
|||
|
|
|
|
|
Замечание 33. В условиях этой теоремы о сходимости ряда Фурье можно говорить на всей числовой оси. О том, что сумма ряда даёт функ-
цию f x , можно говорить только на интервале |
, . Если разлагаемая |
|
функция удовлетворяет ещё дополнительному условию |
||
f |
f , |
|
то из (71) видно, что она будет представима своим рядом Фурье уже на
всём отрезке |
, . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 34. |
Теорема 19 описывает сумму S x |
ряда Фурье на |
||||||||||||||
всём отрезке |
, |
, если функция дифференцируема на этом отрезке. Так |
||||||||||||||
как сумма ряда Фурье 2 |
– периодична, то её значения на отрезке |
, |
||||||||||||||
задают и все остальные её значения на числовой оси. |
|
|
||||||||||||||
Пример 43. |
Требуется |
разложить в |
ряд Фурье |
постоянную |
на |
|||||||||||
, функцию f |
x |
|
|
C . Вычислим её коэффициенты Фурье по форму- |
||||||||||||
лам (70): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
C |
2C , |
|
|
|||
|
a0 |
|
|
|
Cdx |
Cx |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
an |
1 |
|
|
C cos nxdx 0 , bn |
1 |
|
C sin nxdx |
0 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
(при этом воспользовались вычислениями 1 и 2, выполненными при доказательстве теоремы 17). Подставив полученные коэффициенты в (69), по-
лучим |
f x |
~ C . |
Очевидно, что постоянная функция удовлетворяет всем |
||||||||||||
условиям теоремы 19. Так как |
f |
f |
|
C , то согласно этой теореме |
|||||||||||
на |
, |
сумма S x |
ряда будет равна C . Итак, |
f x C и S x |
C на |
||||||||||
всём отрезке |
, . |
|
|
|
|
|
|
|
|
|
|
||||
Пример 44. Найдём ряд Фурье функции f x |
sin x на |
, |
. Со- |
||||||||||||
гласно (70) коэффициенты Фурье таковы: |
|
|
|
|
|
||||||||||
|
a0 |
1 |
|
sin xdx |
1 |
|
cos x |
|
1 |
C cos |
cos |
0 , |
|
||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
93

|
|
an |
1 |
|
sin x cos nxdx |
|
0 , bn |
1 |
|
|
sin xsin nxdx |
|
1 0 при n |
1, |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при n |
1. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При этом при нахождении коэффициентов an |
применено вычисление 5, а |
||||||||||||||||||||||||||||||||||||||
при нахождении bn – 4 и 8. Таким образом, только коэффициент b1 |
1, а |
||||||||||||||||||||||||||||||||||||||
остальные |
|
коэффициенты |
|
ряда |
Фурье |
равны |
нулю. |
Следовательно, |
|||||||||||||||||||||||||||||||
f |
x |
~ sin x и S x |
sin x . Функция |
f |
|
|
x |
|
sin x |
удовлетворяет всем услови- |
|||||||||||||||||||||||||||||
ям |
|
теоремы |
19. |
На интервале |
|
|
|
|
|
|
|
|
, |
|
|
|
S x |
|
даёт |
f |
x . |
Так |
как |
||||||||||||||||
f |
|
sin |
|
|
|
0 , f |
|
sin |
|
|
0 , то согласно замечанию 33 функция |
||||||||||||||||||||||||||||
f |
x |
sin x представима своим рядом Фурье на всём отрезке |
, . При |
||||||||||||||||||||||||||||||||||||
этом по |
равенству (71) |
имеем, |
|
что |
|
S |
|
0 . Итак, |
|
f x |
sin x и |
||||||||||||||||||||||||||||
S x |
sin x на всём отрезке |
|
|
|
, . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Пример 45. Рассмотрим функцию |
f |
x |
x |
на отрезке |
, |
|
. Про- |
||||||||||||||||||||||||||||||
ведём вычисление её коэффициентов Фурье по формулам (70): |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a0 |
|
1 |
|
|
|
xdx |
|
1 |
|
|
x2 |
|
|
|
|
0 , |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
an |
|
x cos nxdx |
|
|
|
x sin nx |
|
|
sin nxdx |
|
0 , |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos n |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
bn |
|
x sin nxdx |
|
|
x cos nx |
|
|
|
|
cos nxdx |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При этом для вычисления коэффициентов an , bn применялась формула интегрирования по частям
b |
b |
||
UdV UV |
|
ba |
VdU |
|
|||
|
|
||
a |
a |
||
и вычисления 1, 2, из доказательства теоремы 17. Так как cos n
 1 n , то bn
1 n , то bn  1 n 1 n2 .
1 n 1 n2 .
Следовательно,
94

x ~ 2 sin x |
sin 2x |
|
sin 3x |
|
sin 4x |
. |
|
|
|
|
|
|
|||
2 |
3 |
4 |
|||||
|
|
||||||
Согласно теореме 19 (функция f x x удовлетворяет условиям этой теоремы), на интервале
x удовлетворяет условиям этой теоремы), на интервале  ,
,  справедливо равенство
справедливо равенство
x |
2 |
sin x |
|
sin 2x |
|
|
sin 3x |
|
sin 4x |
. |
(72) |
|
|
|
|
|
|
|
|
||||||
2 |
3 |
4 |
||||||||||
|
|
|
|
|
||||||||
В точках |
x |
|
и x |
|
|
сумма ряда (72) |
определяется |
|||||
равенством (71): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
0 . |
|
|
|||
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
Это видно непосредственно и из самого ряда (72); все его члены равны ну-
лю при x |
и поэтому его сумма равна нулю. |
||
Так как |
f |
, f |
, а сумма ряда (72) в этих точках равна |
нулю, то равенство (72) при x |
неверно. |
||
Замечание 35. Во всех примерах 43 – 45 сумму S x соответствую- |
|||
щего ряда Фурье по 2 |
-периодичности можно продолжить на всю число- |
||
вую ось (см. замечание 34). Для случая ряда (72) график этой суммы изоб- |
||||||||||
ражён ниже на рисунке. |
|
|
|
y |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
|
x |
|
|
|
3 |
2 |
|
|
|
|
|
|
|
x |
|
0 |
2 |
3 |
4 |
|||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Из графика видно, что сумма S x ряда Фурье функции f x
ряда Фурье функции f x x
x
совпадает с этой функцией только на интервале |
, |
. Вне этого интер- |
||||||||
вала графики f x |
x |
и S x |
не имеют ни одной общей точки. Например, |
|||||||
в точке |
имеем: |
f |
, |
S |
0 . Отметим ещё, |
что все члены ряда |
||||
(72) непрерывны, а его сумма S x |
является функцией разрывной. |
|||||||||
Теорема 19 уже не подходит для функции |
f x |
|
x |
|
, рассматривае- |
|||||
|
|
|||||||||
мой на отрезке |
, |
, т.к. эта функция в точке x |
0 не имеет производ- |
|||||||
ной. Приведём более общую теорему о сходимости ряда Фурье и о пред-
95

ставлении его суммой значений |
f |
x на |
, |
. Эта теорема также даёт |
||
достаточные условия для такого представления. |
|
|
||||
Теорема 20 (Дирихле). Пусть функция f |
x удовлетворяет следую- |
|||||
щим условиям: |
|
|
|
|
|
|
1) имеет на интервале |
, |
разве лишь конечное число точек раз- |
||||
рыва первого рода; |
|
|
|
|
|
|
2) имеет конечный правосторонний предел |
f |
0 в точке x |
||||
и конечный левосторонний предел |
f |
0 в точке x |
; |
|||
3) отрезок |
, можно разбить на конечное число интервалов, на |
|||||
каждом из которых функция монотонна (либо неубывающая, либо невозрастающая).
|
Тогда ряд Фурье функции |
f x сходится на отрезке |
, . При |
|||||||||||||
этом его сумма S x |
удовлетворяет равенствам: |
|
|
|||||||||||||
|
а) |
S x0 |
|
f |
x0 |
|
|
|
|
|
|
|
|
(73) |
||
в каждой точке x0 |
из |
, |
, в которой функция непрерывна; |
|
||||||||||||
|
б) |
S x0 |
|
f |
|
x0 |
0 |
f x0 |
0 |
|
|
|
|
|
(74) |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в точках разрыва из |
, |
; |
|
|
|
|
|
|
|
|||||||
|
в) |
S |
|
|
f |
|
|
0 |
f |
0 |
. |
|
|
|
(75) |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 36. Поскольку члены ряда Фурье являются периодиче- |
|||||||||||||||
скими функциями с периодом 2 |
, то из теоремы Дирихле следует сходи- |
|||||||||||||||
мость ряда Фурье на всей числовой оси |
|
, |
при наличии у функции |
|||||||||||||
указанных в теореме свойств. |
|
|
|
|
|
|
|
|||||||||
|
Замечание 37. Если сама функция |
f |
x , по которой составлен ряд |
|||||||||||||
Фурье, является 2 |
|
-периодичной, то утверждения теоремы 20 справедли- |
||||||||||||||
вы |
не |
только на |
промежутке |
, |
, |
но и |
в любом |
промежутке |
||||||||
2k |
1 |
, 2k |
1 |
|
|
|
, где k |
1, |
2, .... Таким образом, тригонометрический |
|||||||
ряд Фурье 2 |
-периодической функции описывает её всюду в том смысле, |
|||||||||||||||
как это сформулировано в теореме Дирихле. |
|
|
|
|||||||||||||
96

Замечание 38. Если функция f x , по которой составлен ряд Фурье, определена на всей числовой оси, но не является периодической, то вне
промежутка |
, утверждения теоремы Дирихле не имеют места. Непе- |
|||
риодическая функция |
f x и сумма S x её ряда Фурье (периодическая |
|||
функция) вне отрезка |
, не имеют ничего общего. |
|||
|
|
|||
Пример 46. Требуется разложить в ряд Фурье функцию f x |
x |
, |
||
заданную на отрезке |
, . Ещё раз напомним, что эта функция, хотя и |
|||
непрерывна на этом отрезке, но дифференцируемой на нём не является. Довольно простая теорема 19 к ней неприменима. Условиям теоремы 20 эта функция удовлетворяет. Она имеет два интервала монотонности: на
, 0 убывает, а на 0, |
|
возрастает. |
Для вычисления коэффициентов |
|
Фурье функцию запишем следующим образом: |
||||
f |
x |
x при |
x 0, |
|
x при |
0 x . |
|||
|
|
|||
Найдём её коэффициенты Фурье по формулам (70):
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
x dx |
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
an |
1 |
|
|
|
0 |
|
|
x cos nxdx |
|
|
x cos nxdx |
|
1 |
|
|
|
|
xsin nx |
|
0 |
|
1 |
|
0 |
sin nxdx |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos nx |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
xsin nx |
|
|
1 |
sin nxdx |
1 1 |
|
|
|
cos nx |
|
|
|
|
2 |
|
|
cos n |
1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
0 |
|
|
|
n |
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
0 |
|
|
|
n2 |
||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
при чётном n, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
при нечётном n; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos n |
|
|
|
|
|
|
|
|
|
|
cos n |
|
|
|
||||||||
|
|
bn |
|
|
x sin nxdx |
x sin nxdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При вычислении an и bn |
применялся метод интегрирования по частям. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подставив эти коэффициенты в (69), |
|
получим |
на |
всём |
отрезке |
|||||||||||||||||||||||||||||||||||||||||||||||||
, |
следующее представление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
97

|
x |
|
|
|
|
4 |
cos x |
cos3x |
|
cos5x |
|
cos 7x |
. |
(76) |
|||
|
|
|
|
||||||||||||||
|
|
2 |
|
3 |
2 |
5 |
2 |
7 |
2 |
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как функция непрерывна на |
|
, , то для суммы ряда действуют |
|||||||||||||||
утверждения а) и б) теоремы 20.
Представление (76) будет верно на всей числовой оси, если функцию
f x |
x |
продолжить с отрезка |
, на всю ось с периодом 2 (предо- |
|
|
|
|
ставляем читателю построить графики этой ситуации самостоятельно). Изучим теперь особенности ряда Фурье чётной и нечётной функций. Функция x , определённая на симметричном относительно нуля
промежутке, называется чётной, если на этом множестве выполняется равенство
x |
x , |
и нечётной, если |
|
x |
x |
для всех x из этого промежутка. |
|
В интегральном исчислении имеются два фактически очевидных
утверждения: |
|
|
|
|
|
1) если |
x |
чётна на отрезке |
a, a , то |
|
|
|
|
a |
a |
|
|
|
|
x dx |
2 |
x dx ; |
(77) |
|
|
a |
0 |
|
|
2) если |
x |
нечётна на a, a , то |
|
|
|
|
|
a |
|
|
|
|
|
x dx |
0 . |
(78) |
|
a
Эти два равенства легко понять с геометрической точки зрения. При этом надо учитывать следующее: интеграл от модуля функции даёт площадь соответствующей криволинейной трапеции; график чётной функции симметричен относительно оси ординат; график нечётной функции симметричен относительно начала координат.
Пусть на отрезке 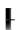 ,
, 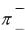 разлагаемая в ряд функция f x
разлагаемая в ряд функция f x является чётной. Тогда ей соответствует ряд Фурье
является чётной. Тогда ей соответствует ряд Фурье
98

|
|
f |
x |
~ |
a0 |
a |
cos nx , |
(79) |
|
||||||||
|
|
|
|
2 |
n |
|
|
|
|
|
|
|
n 1 |
|
|
||
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
||
2 |
|
|
|
|
|
n 0,1, 2, ... . |
(80) |
|
an |
|
|
f |
x cos nxdx |
||||
|
||||||||
0 |
|
|
|
|
|
|
||
Формула (79) позволяет говорить, что ряд Фурье чётной функции содержит только косинусы.
Проведём доказательнство этого утверждения. Напомним, что коэффициенты ряда Фурье вычисляются по формулам (70). Так как функция f x чётна, а sin nx есть нечётная функция, то произведение f x sin nx не-
чётна, а sin nx есть нечётная функция, то произведение f x sin nx не-
чётно и поэтому из (78) следует, что все коэффициенты bn равны нулю:
|
|
|
|
|
|
|
|
|
bn |
1 |
|
f |
x sin nxdx |
0 . |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Так как f |
x чётна и функция cosnx чётна, то функция f |
x cos nx |
чётна и |
|||||||||||||||||||||||||||||||||
поэтому равенство (80) следует из (77). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Пример 47. Требуется разложить в ряд Фурье функцию f x |
x2 на |
||||||||||||||||||||||||||||||||||
отрезке |
, . Так как эта функция чётна, то надо вычислить только ко- |
|||||||||||||||||||||||||||||||||||
эффициенты an по формуле (80). Проведём эти вычисления: |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a0 |
|
2 |
|
x2dx |
|
2 |
|
|
x3 |
|
|
|
2 |
2 |
|
; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
x2 cos nxdx |
2 |
1 |
|
x2 sin nx |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
an |
|
|
|
|
|
|
|
|
|
|
|
|
2 xsin nxdx |
|
x sin nxdx |
|||||||||||||||||||||
|
|
|
|
|
n |
0 |
n |
|||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|||||||||||||
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
4 |
cos n |
||||||||||||||||
|
|
|
x cos nx |
0 |
|
cos nxdx |
|
|
|
|
|
x cos nx |
|
0 |
cos n |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
n2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
n2 |
|
|
n2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(при вычислении an |
два раза проводилось интегрирование по частям). Так |
|||||||||||||||||||||||||||||||||||
как cosn |
1 при чётных номерах n и cosn |
|
|
1 при нечётных n , то |
||||||||||||||||||||||||||||||||
cos n |
1 n . Тогда an |
|
|
|
|
1 n |
4 |
. Подставляя найденные коэффициен- |
||||||||||||||||||||||||||||
|
|
|
|
n2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ты в (79), получим
99

|
|
|
|
x2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 n |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos nx . |
|
|
|
||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
n |
1 |
|
|
|
n2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Функция этого примера удовлетворяет условию теоремы 19, причём |
|||||||||||||||||||||||||||||||||||||||||||||
f |
f |
(см. замечание |
|
33). Поэтому |
|
на |
, |
справедливо |
||||||||||||||||||||||||||||||||||||||
равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
2 |
|
|
|
|
|
|
cos x |
|
|
|
cos 2x |
cos3x |
|
cos 4x |
|
|
|
|||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
, |
(81) |
|||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
12 |
|
|
|
|
|
|
|
|
22 |
|
|
|
|
32 |
|
|
|
42 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
при этом S |
2 (см. (71)). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Из функционального равенства (82) выведем одно интересное равен- |
|||||||||||||||||||||||||||||||||||||||||||||
ство для числовых рядов. Положив в (81) |
|
x |
|
, получим |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||||||
|
|
3 |
|
12 |
|
22 |
|
|
32 |
|
|
42 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
откуда вытекает равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
n 1 n2 |
|
|
|
12 |
|
|
|
22 |
32 |
|
42 |
|
|
|
|
6 |
|
|
|
|||||||||||||||||||||||||
|
Пусть теперь разлагаемая в тригонометрический ряд функция |
f x |
||||||||||||||||||||||||||||||||||||||||||||
является нечётной на отрезке |
|
|
|
, . Тогда ей соответствует ряд Фурье |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
x ~ |
|
|
|
bn sin nx , |
|
|
|
|
|
|
|
(82) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0,1, 2, ... . |
|
|
|
(83) |
|||||||||||||||||
|
|
bn |
|
|
|
|
|
|
|
f x sin nxdx |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Формула (82) означает, что ряд Фурье нечётной функции не содержит ни свободного члена, ни косинусов (разложение происходит только по синусам).
Доказательство этого утверждения предоставляем читателю. Оно аналогично предыдущим рассуждениям, проведённым для чётной функции, и снова опирается на равенства (77) и (78).
100

Пример 48. Требуется разложить в ряд Фурье функцию f x x на
x на
отрезке |
, . |
Так как функция является нечётной, то представление |
|||||||||
имеет вид (82). Коэффициенты bn |
вычисляются по формуле (83): |
||||||||||
|
2 |
|
|
2 |
|
1 |
|
|
|
||
|
bn |
|
|
x sin nxdx |
|
|
|
|
x cos nx |
0 |
cos nxdx |
|
|
|
|
|
|
n |
|||||
|
|
|
0 |
|
|
|
|
0 |
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
2 |
cos n |
|
|
sin nx |
|
|
|
|
2 |
cos n |
1 |
n |
1 |
2 |
. |
||||
|
|
n |
|
|
n |
|
0 |
|
n |
|
|
n |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставив найденные коэффициенты в (82), получим |
|
|
|
|
|
|||||||||||||||
|
|
|
x ~ 2 |
sin x |
|
sin 2x |
|
|
sin 3x |
|
|
sin 4x |
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
2 |
3 |
|
|
4 |
|
|
|
|
|
|
||||||
На |
, будет верно равенство (72). |
|
|
|
|
|
|
|
|
|
||||||||||
Заметим, что функция уже рассматривалась в примере 45 согласно общему случаю (69), (70). Теперь нечётность функции позволила упростить вычисления.
Перейдём к изучению разложения в ряд Фурье функции, заданной на
части отрезка |
, |
. Речь идёт о частях |
, a и a, |
, где |
a |
. |
Здесь ограничимся рассмотрением частного случая, а именно отрезка |
||||||
0, . Рассуждения, |
аналогичные дальнейшим, читатель может провести |
|||||
для отрезка |
, 0 . |
|
|
|
|
|
Итак, пусть функция f x определена на отрезке |
0, . Чтобы разла- |
|||||
гать её в ряд (69) (с коэффициентами, найденными по формулам (70)), нужно получить функцию, заданную на всём отрезке  , . Таким образом, мы должны функцию f x
, . Таким образом, мы должны функцию f x доопределить. Иначе говоря, необходимо продолжить функцию на промежуток
доопределить. Иначе говоря, необходимо продолжить функцию на промежуток  , 0 . Отметим, что такое продолжение не является однозначным. Очевидно, что продолжить заданную функцию можно бесконечным множеством способов. Однако надо делать
, 0 . Отметим, что такое продолжение не является однозначным. Очевидно, что продолжить заданную функцию можно бесконечным множеством способов. Однако надо делать
такие продолжения, чтобы новая функция g x на всём отрезке |
, |
|
удовлетворяла условиям теоремы 19 или теоремы Дирихле. |
|
|
После такого продолжения (доопределения) новую функцию |
g x , |
|
заданную на всём отрезке |
, , будем разлагать в ряд Фурье на этом |
|
|
101 |
|

отрезке. Так как реально заданной является только часть этой новой функции, т.е. функция f x на 0, , то полученный тригонометрический ряд
на 0, , то полученный тригонометрический ряд
будем рассматривать только для значений переменной x из |
0, . |
Этот |
|
трегонометрический ряд уже нельзя называть рядом Фурье функции |
f |
x , |
|
так как само понятие ряда Фурье рассматривалось на отрезке |
, |
, |
а не |
на 0, . Коэффициенты Фурье функции g x будем считать коэффициен-
будем считать коэффициен-
тами соответствующего тригонометрического ряда функции f x |
на 0, . |
|||
Наиболее |
применяемыми |
являются |
следующие |
способы |
продолжения: |
|
|
|
|
1)продолжение f x на
на  , 0
, 0 по чётности;
по чётности;
2)продолжение f x на
на  , 0
, 0 по нечётности.
по нечётности.
|
В первом случае получим нечётную |
функцию |
g x |
на |
отрезке |
|||||||
, |
. Её разложение будет иметь вид (79), а коэффициенты an будут |
|||||||||||
вычеслены по формуле (80). Так как g x |
f |
x |
на |
0, |
, |
то получится |
||||||
разложение f |
x в тригонометрический ряд на |
0, |
. Вопрос наличия ра- |
|||||||||
венства S x |
f x выясняется с помощью теорем 19 или 20. |
|
|
|||||||||
|
Во втором случае будем иметь дело с нечётной функцией |
g x на |
||||||||||
, |
. Её разложение будет иметь вид (82). Коэффициенты bn |
разложе- |
||||||||||
ния будут вычисляться по формуле (83). Так как g x |
f |
x на 0, |
, то на |
|||||||||
самом деле получится разложение f x |
в тригонометрический ряд по си- |
|||||||||||
нусам на 0, |
. Если |
g x |
будет удовлетворять условию теоремы 19, то |
|||||||||
сходимость ряда к f x |
будет соблюдена на интервале |
0, |
. Сходимость |
|||||||||
ряда (82) к значениям |
f x |
в точках x |
0 и x |
|
будет зависеть от значе- |
|||||||
ний функции f |
x в этих точках. Так как ряд (82) обращается в нуль в точ- |
|||||||||||
ках x |
0 и x |
, то для выполнения равенства |
S 0 |
|
f 0 |
надо, чтобы |
||||||
f 0 |
0 , а для выполнения равенства S |
f |
|
надо, чтобы f |
0 . |
|||||||
|
На самом деле при разложении f |
x , заданной на |
0, |
, в тригоно- |
||||||||
метрический ряд (79) или (82) (только по косинусам или только по сину-
сам) нет необходимости фактически |
осуществлять её продолжение на |
, 0 . После продолжения для g x |
нужно применять формулы (80) или |
102

(83). В этих формулах интегрирование проводится по отрезку |
0, , на ко- |
|||||
тором g x |
f x . |
|
|
|
|
|
Способ |
продолжения f x до g x |
имеет |
значение |
только |
при |
|
нахождении суммы S x полученного ряда в точках x |
0 и x |
. |
|
|||
Пример 49. Требуется разложить функцию |
f x |
x , |
заданную на |
|||
0, в какой-нибудь тригонометрический ряд. |
|
|
|
|
||
Сначала продолжим эту функцию на |
, 0 |
чётным образом, |
т.е. |
|||
будем разлагать в тригонометрический ряд по косинусам. Новая функция
g x |
будет задана на |
, |
|
и иметь вид |
g x |
x |
. Разложение |
x |
в ряд |
|||||||
Фурье проведено в примере 46 и имеет вид (76). За разложение f |
x |
x на |
||||||||||||||
0, |
примем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ~ |
4 |
|
cos x |
|
cos3x |
|
cos5x |
. |
|
(84) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
12 |
32 |
|
52 |
|
|
|||||||
Конечно, коэффициенты этого разложения можно было бы найти по формуле (80), положив в ней f x x , получили бы то же самое представление
x , получили бы то же самое представление
(84).
|
Остаётся |
выяснить, |
какую |
|
функцию задаёт ряд |
(84). Функция |
||||||||||||||||||||||||
g x |
|
x |
|
на |
, удовлетворяет условиям теоремы Дирихле. Так как она |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
непрерывна (в том числе и при x |
|
|
0 ), то в каждой точке непрерывности |
|||||||||||||||||||||||||||
S x |
g x (тогда S 0 |
g 0 |
|
|
|
0 ). По условию (75) |
|
|
||||||||||||||||||||||
|
|
|
|
|
S |
|
g |
0 |
|
|
g |
0 |
|
|
|
|
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Тогда при 0 |
x |
будет |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
4 |
|
|
|
cos x |
|
|
cos3x |
|
cos5x |
, |
(85) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
32 |
52 |
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
при этом S 0 |
0 , |
S |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Положив в (85) x |
0 , получим сумму интересного числового ряда: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
12 |
32 |
|
|
52 |
|
8 |
|
|
|
|||||||||||||
103

Продолжим теперь функцию этого примера на промежуток |
, 0 |
нечётным образом, т.е. будем разлагать в тригонометрический ряд по синусам. Новая функция g x будет задана на
будет задана на  ,
,  и иметь вид g x
и иметь вид g x x . Её разложение в ряд Фурье проведено в примерах 45 и 48. Его же примем
x . Её разложение в ряд Фурье проведено в примерах 45 и 48. Его же примем
за разложение f x x на 0, |
: |
|
|
|
|
|
|
||
x ~ 2 |
sin x |
|
sin 2x |
|
sin 3x |
|
sin 4x |
. |
(86) |
1 |
|
2 |
3 |
4 |
|||||
|
|
|
|
||||||
Отметим, что это разложение можно было бы найти по (82) и (83), положив в этих формулах f x x .
x .
Выясним, какую функцию задаёт тригонометрический ряд (86) на промежутке 0, . Так как функция g x x дифференцируема на
x дифференцируема на  ,
,  , то по теоерме 19 в каждой точке этого интервала выполняется равенство
, то по теоерме 19 в каждой точке этого интервала выполняется равенство
S x g x . При этом S 0 g 0 |
f 0 |
0 . Так как g x f x на 0, , то |
|||
ряд (86) на 0, представляет функцию |
f x x . Согласно (71) |
||||
S |
g |
g |
|
|
0 . |
|
|
|
|
||
|
2 |
2 |
|||
|
|
|
|||
Впрочем, это видно и из самого ряда (86). Следовательно, в точке x  значение суммы ряда не совпадает со значением функции f x
значение суммы ряда не совпадает со значением функции f x x в этой точке
x в этой точке  f
f 

 . Таким образом, равенство
. Таким образом, равенство
x |
2 |
|
sin x |
|
sin 2x |
|
sin 3x |
|
sin 4x |
|
1 |
2 |
3 |
4 |
|
||||||
|
|
|
||||||||
справедливо только на полуотрезке |
0, . |
|
|
|
||||||
До сих пор вся теория рядов Фурье излагалась для функций, задан- |
||||||||||
ных на отрезке |
, |
. Их можно рассматривать и для 2 -периодических |
||||||||
функций, определённых на всей числовой оси, значения которых задаются
одним из промежутков |
, , |
, , |
, , |
, . Прежде всего |
дело в том, что число T 2 |
есть период всех функций тригонометриче- |
|||
ской системы (63). Кроме того, эта система обладает важнейшим свойством на  , – свойством ортогональности (см. определение 15 и теорему 17).
, – свойством ортогональности (см. определение 15 и теорему 17).
104

Коэффициенты an , bn ряда Фурье функции f x вычисляются согласно формулам (70) путём интегрирования по отрезку
вычисляются согласно формулам (70) путём интегрирования по отрезку  ,
,  выражений, сомножителями которых являются функции тригонометрической системы (63). Члены самого тригонометрического ряда (69) формируются с помощью коэффициентов Фурье (70) и функций всё той же системы (63).
выражений, сомножителями которых являются функции тригонометрической системы (63). Члены самого тригонометрического ряда (69) формируются с помощью коэффициентов Фурье (70) и функций всё той же системы (63).
Оказывается, что система (63) ортогональна (см. определение 15) на всяком отрезке длины 2 и при всяком a справедливы равенства
a 2 |
|
a |
2 |
|
|
|
cos2 nxdx |
, |
sin 2 nxdx |
. |
(87) |
a |
|
|
a |
|
|
Это позволяет всю теорию этого параграфа перенести с отрезка |
, на |
||||
любой отрезок a, a |
2 , т.е. произвести сдвиг основного промежутка |
||||
, на величину a |
. |
|
|
|
|
Доказательство этих фактов основано на следующей теореме. Теорема 21. Для периодической функции с некоторым периодом T
функции x при любых a и |
справедливо |
|
|
a T |
a |
T |
|
|
x dx |
x dx . |
|
a |
a |
|
|
Частным случаем этого равенства является следующее |
|
||
a 2 |
|
|
|
|
x dx |
x dx . |
(88) |
a |
|
|
|
Аналитическое доказательство теоремы 21 представляем провести |
|||
читателю. Заметим только, что в случае |
x 0 равенство (88) имеет про- |
||
стой геометрический смысл. Оно означает, что площади криволинейных
трапеций, образуемые периодической функцией |
x , по отрезку |
, и |
сдвинутому отрезку a, a 2 той же длины 2 |
совпадают (рекомендуем |
|
читателю сделать рисунок). |
|
|
Тогда ортогональность системы (63) на отрезке a, a 2 |
очевидым |
|
образом вытекает из теоремы 17 и равенства (88). Из равенства (88) и вычислений 7, 8 из доказательства теоремы 17 следуют равенства (87).
Определение 17. Числа an , bn , определённые равенствами
105

|
1 a |
2 |
|
|
0,1, 2, ... , |
(89) |
|||
an |
|
|
|
|
f x cos nxdx |
n |
|||
|
|
||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
1 a |
2 |
|
n |
1, 2, ... , |
(90) |
||
bn |
|
|
f |
x sin nxdx |
|||||
|
|||||||||
|
|
|
|
|
a |
|
|
|
|
называются коэффициентами |
Фурье функции f x |
по промежутку |
|||||||
a, a 2 .
Определение 18. Функциональный ряд
f x ~ |
a0 |
|
a |
n |
cos nx |
b sin nx , |
(91) |
|
|
||||||
2 |
|
|
|
n |
|
||
n |
1 |
|
|
|
|
||
|
|
|
|
|
|
||
образуемый с помощью коэффициентов, вычисленных по формулам (89),
(90), называется рядом Фурье функции f x |
по отрезку a, a |
2 . |
Для этого ряда справедливы |
утверждения, |
аналогичные |
теоремам 19 и 20.
Пример 50. Требуется разложить в ряд Фурье функцию f x x , рассматриваемую на отрезке 0, 2 . Проведём вычисление коэффициентов по формулам (89), (90):
x , рассматриваемую на отрезке 0, 2 . Проведём вычисление коэффициентов по формулам (89), (90):
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
x2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
a0 |
xdx |
|
|
|
|
|
2 |
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
||||||||
|
an |
x cos nxdx |
|
|
|
x sin nx |
|
|
|
|
|
|
|
sin nxdx |
|
|
|
cos nx |
0 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
b |
x sin nxdx |
|
|
|
|
x cos nx |
|
|
|
|
cos nxdx |
|
|
|
2 |
cos 2 |
n |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
sin nx |
|
02 |
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Согласно (91), ряд Фурье исследуемой функции на отрезке |
0, 2 |
|
будет |
||||||||||||||||||||||||||||||||||||||||
иметь вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x ~ |
|
|
2 |
|
sin x |
|
sin 2x sin 3x |
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
106

При этом на интервале 0, 2 согласно теореме, аналогичной теореме 19, будет выполняться равенство
согласно теореме, аналогичной теореме 19, будет выполняться равенство
|
|
x |
2 |
|
sin x |
|
|
|
sin 2x |
|
|
sin 3x |
. |
(92) |
||||
|
1 |
|
|
|
2 |
|
|
|
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Положив |
x |
|
в равенстве (92), получим числовое равенство |
|
||||||||||||||
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
|
, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
3 |
5 |
|
7 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
дающее сумму ряда, которую ранее применявшимися методами в [7] мы
получить не могли. |
|
|
|
|
По равенству, аналогичному (71), получим сумму ряда в точках x |
0 |
|||
и x 2 ; она равна числу |
. Так как f 0 0 , f 2 |
2 , то сумма ряда в |
||
этих точках не совпадает со значениями функции в них. |
|
|||
Замечание 39. |
В примере 45 дано разложение функции f x |
x в |
||
ряд Фурье на отрезке |
|
, , а в примере 50 – разложение той же по виду |
||
функции на отрезке |
0, 2 |
. Их ряды (см. примеры 45 и 50) совершенно |
||
различны, так как порождаются разными функциями (аналитическое выражение функции одно и то же, а промежутки её задания различны). Эти
функции |
совпадают лишь |
на отрезке 0, . Продолжения функции |
f x x |
из основного отрезка |
, на всю числовую ось с периодом 2 |
и из отрезка 0, 2 на всю числовую ось с периодом 2 – различны. Естественно, что и соответствующие ряды на всей числовой оси являются разными.
на всю числовую ось с периодом 2 – различны. Естественно, что и соответствующие ряды на всей числовой оси являются разными.
Замечание 40. Сдвиг промежутка не столь важен с теоретической точки зрения, но может оказаться полезным при вычислении коэффициентов ряда Фурье 2 – периодической функции, заданной на всей числовой
оси, со значениями, определяемыми отрезком |
|
, . |
|||
Пример 51. Требуется разложить в ряд Фурье 2 – периодическую |
|||||
функцию, заданную на основном отрезке |
, |
следующим образом: |
|||
f x |
x 2 |
при |
x |
0, |
|
x |
при 0 |
x . |
|||
|
|||||
107

Вычисление коэффициентов Фурье этой функции по формулам (70)
неудобно, так как на отрезку |
, функция имеет разрыв в точке x 0 |
||||
поэтому |
промежуток интегрирования придётся |
разбить на две части: |
|||
, 0 , |
0, . Продолжим эту функцию по 2 – |
периодичности на всю |
|||
числовую ось (см. рисунок ниже). |
|
|
y |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
0 |
2 |
3 |
x |
|
Тогда значения исходной функции можно задать равенством f x |
x |
на |
полуотрезке 0, 2 . Такое задание неверно для точки x 0 . Если |
f x |
x |
будем разлагать в ряд Фурье на отрезке 0, 2 , то разрыв функции на левом конце x 0 этого промежутка не будет влиять на разложение в ряд Фурье.
Таким образом, согласно изложенной выше теории, коэффициенты ряда Фурье можно вычислять по формулам (89), (90) с промежутком интегрирования 0, 2 , на котором функция непрерывна, вместо формул (70) с
промежутком интегрирования |
, , на котором функция |
раз- |
рывна. |
|
|
Проведём вычисление коэффициентов по формулам (89), (90) с про-
межутком интегрирования |
0, 2 |
: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 2 |
|
1 |
|
x2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a0 |
|
xdx |
|
|
|
|
|
|
|
|
2 , |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
1 |
|
2 |
2 |
|
||||
a |
|
|
x cos nxdx |
0 |
, b |
|
|
|
|
|
xsin nxdx |
|
. |
||||
n |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ряд Фурье исходной функции на отрезке  ,
,  имеет вид
имеет вид
108

f x ~ |
2 |
sin x |
|
|
sin 2x |
|
sin 3x |
. |
|
|
1 |
|
2 |
|
3 |
|
|
||||
|
|
|
|
|
|
|
||||
Представляем читателю выяснить, |
в каких точках отрезка |
, |
имеет |
|||||||
место равенство |
|
|
|
|
|
|
|
|
|
|
|
|
S x |
|
f x . |
|
|
|
|
||
Замечание 41. Конечность промежутка задания функции является определяющим фактором вида её ряда Фурье.
Таким образом, развитая в этом параграфе теория, является хорошим аналитическим аппаратом для выражения функций, заданных на промежутке длины 2 , через тригонометрические функции. Эта теория дала но-
вые методы вычисления сумм числовых рядов. |
|
|||
|
Перейдём теперь к функциям, заданным на отрезке другой длины. |
|||
Именно, будем рассматривать функции f x , |
определённые на отрезке |
|||
l, l |
, где l – произвольное положительное число. Сразу будем предпола- |
|||
гать, |
что функция f x на этом промежутке удовлетворяет условиям тео- |
|||
ремы 19 или условиям теоремы Дирихле. |
|
|||
|
Введём замену переменной по формуле |
|
||
|
t |
|
x . |
(93) |
|
l |
|||
Из формулы (93) видно, что если переменная x пробегает в возрастающем
порядке значения от |
l |
до l , то переменная t в возрастающем порядке |
||||||
принимает значения из отрезка |
|
, . |
|
|
||||
Обозначим через |
t ту функцию, в которую преобразуется функ- |
|||||||
ция f x при замене переменной по формуле (93): |
|
|||||||
|
|
t |
f |
|
l |
t |
f x . |
(94) |
|
|
|
|
|||||
Функция t , |
определённая уже на отрезке |
, , будет на этом |
||||||
отрезке удовлетворять условиям теоремы 19 или теоремы Дирихле, так как линейная замена переменной (93) не может привести к нарушению требований этих теорем.
Ряд Фурье функции t  на отрезке
на отрезке  ,
,  будет иметь вид
будет иметь вид
109

|
t |
~ |
|
a0 |
|
|
|
|
|
a |
n |
|
cos nt |
b |
sin nt |
|
(95) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
с коэффициентами, определяемыми формулами |
|
|
|
|
||||||||||||||||||||||||
an |
|
|
1 |
|
|
|
|
|
f t |
cos ntdt |
n |
0,1, 2, ... , |
(96) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1 |
|
|
||||||||||||||||||||||||
bn |
|
|
|
|
|
f |
t sin ntdt |
n |
1, 2, ... . |
|
(97) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вернёмся теперь от переменной t обратно к переменной x . В силу |
||||||||||||||||||||||||||||
(93), (94) представление (95) примет вид |
|
|
|
|
|
|
||||||||||||||||||||||
f x ~ |
a0 |
|
|
|
|
|
a |
n |
cos |
n |
x |
b |
sin |
n |
x . |
(98) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
n |
|
l |
|
|
||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Формулы (96) и (97) примут следующий вид: |
|
|
|
|
|
|||||||||||||||||||||||
an |
1 l |
f |
x cos |
nπ |
xdx |
n |
0,1, 2, ... , |
(99) |
||||||||||||||||||||
l |
|
|
|
l |
|
l |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
b |
|
|
1 l |
|
f |
|
x sin |
nπ |
xdx |
n |
1, 2, ... . |
(100) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n |
|
|
|
l l |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При переходе от равенств (96), (97) к соответствующим равенствам (99), (100) применён метод замены переменной в определённом интеграле.
Читателю поясним следующее: в силу равенства (93) имеем, что dt |
|
dx ; |
||
l |
||||
при t |
и t |
имеем соответственно, что x l , x l . |
|
|
|
Таким образом, представление (98) задаёт ряд Фурье функции |
f x |
||
на отрезке  l, l , коэффициенты этого представления определяются равенствами (99) и (100).
l, l , коэффициенты этого представления определяются равенствами (99) и (100).
Сходимость ряда (98) и его сумма устанавливаются на основании теорем, аналогичных теоремам 19 и 20.
Если f x –чётная функция на отрезке  l, l
l, l с периодом 2l , то
с периодом 2l , то
f x ~ |
a0 |
|
|
an cos |
nπ |
x , |
|
|
|
|
|||
2 |
n |
1 |
|
l |
||
|
|
|
|
|
||
где
110

|
|
2 l |
|
|
|
nπ |
|
|
|
|
|
|
n |
0,1, 2, ... . |
|
||||||||
an |
|
|
|
|
f |
|
x cos |
|
|
|
|
xdx |
|
||||||||||
|
l |
|
|
|
l |
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если f x –нечётная функция на отрезке |
l, l |
с периодом 2l , то |
|||||||||||||||||||||
|
|
|
|
|
f |
x ~ |
|
|
|
|
b |
|
|
sin |
nπ |
x , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
l |
|
|
|
|||
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
2 l |
f |
x sin |
nπ |
xdx |
n |
1, 2, ... . |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n |
|
|
l 0 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 52. Требуется разложить функцию |
f x |
x на интервале |
|||||||||||||||||||||
2, 2 в ряд Фурье. Данная функция нечётная. Здесь l |
2 , тогда имеем: |
||||||||||||||||||||||
|
x |
|
|
|
|
b sin |
nπ |
x на |
2, 2 , |
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
n |
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b |
|
|
|
xsin |
xdx |
n |
1, 2, ... . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
n |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдём bn :
|
2 |
nπ |
|
|
2 |
|
nx |
|
b |
xsin |
xdx |
x |
cos |
||||
|
|
|
||||||
n |
|
2 |
|
|
n |
2 |
||
|
0 |
|
|
|||||
|
|
|
|
|
|
|
||
2 |
2 |
|
2 |
sin |
nx |
|
|
2 |
4 |
cos n |
4 |
1 n 1, |
|
||||||||||||
0 |
n |
|
n |
2 |
|
0 |
n |
n |
||||
|
|
|
|
|
||||||||
n 1, 2, ... .
Тогда
|
|
|
sin |
|
x |
|
|
sin |
|
2 x |
|
|
x |
4 |
|
2 |
2 |
|
. |
||||||
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|||||
111
