
ekz_terver_zima
.pdf
1. Характеристическая и производящая функции
1. Характеристической функцией случайной величины ξ называется функция: ( ) =
|
где = . |
|
|
|
|
|
|
|
Если случайная величина ξ дискретна, то ( ) = ∑ |
∞ |
|
|
∞ |
|
{ξ = x |
} = 1. |
|
=−∞ |
, где ∑ |
=−∞ |
||||||
|
|
|
|
|
k |
|
||
Если случайная величина ξ абсолютно непрерывна, то ( ) = ∫−∞∞ ( ) (в общем виде:
( ) = ∫−∞∞ ( )).
2. Теорема о существовании характеристической функции.
Характеристическая функция любой случайной величины существует.
Док-во. Пусть ξ – случ.вел. с функцией распределения ξ(x). Рассмотрим ( ) = . По свойствам случ.вел., если | | < +∞, то < +∞, то есть мат.ожидание существует. Тогда
| | = | | = |cos ξ + i sin ξ| = √cos2 ξ + sin2 ξ = 1 = 1.
< +∞ => характеристическая функция существует.
3. Свойства характеристической функции: 1) (0) = 1, | ( )| ≤ 1
2)̅̅̅̅̅̅
(− ) = ( )
3)Характеристическая функция ( ) равномерно непрерывна по .
4)Если ξ1, … , ξ – независимые случ.вел, то характ. функция суммы независимых случ.вел. равна произведению характ.функций.
5)Если случ.вел. ξ имеет n начальных моментов вплоть до степени n включительно ( |ξn| < +∞), то ее характ.ф-ция ξ( ) имеет n первых производных и ( )( ) = ξk 0 ≤ ≤ .
6)Если = ξ + b, то ( ) = + ξ( ), где ξ( ) – характ.ф-ция случ.вел. ξ.
4. Теорема о равномерной непрерывности характеристической функции.
Характеристическая функция ( ) равномерно непрерывна по .
Док-во. По определению равномерной непрерывности докажем: > 0 ( ) >
0 | 1 − 2| < |
| ( 1) − ( 2)| < . |
|
|
|
|
|
||||
|
|
|
|
∞ |
|
∞ |
|
∞ |
|
|
| ( |
|
) − ( |
)| = |∫ |
1 ( ) − ∫ |
2 ( )| = |∫ |
2 ( (1−2) − 1) ( )| ≤ |
||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
−∞ |
|
−∞ |
|
|
||
∞ |
|
|
|
|
|
|
|
|
|
|
≤ ∫ |
| 2 || (1−2) |
− 1| ( ) = ∫ |
|
| (1−2) − 1| ( ) + ∫ |
| (1−2) − 1| ( ) |
|||||
−∞ |
|
|
|
|
| |> |
|
|
| |≤ |
|
|
|
|
= 1 + 2 |
|
|
|
|
|
|
|
|
I1: | (1−2) − 1| = |cos( |
− ) + sin( |
|
− ) − 1| = |
|
|
|||||
|
|
|
|
1 |
2 |
1 |
2 |
|
|
|
√(cos( 1 − 2) − 1) + sin2( 1 − 2) = √2 − 2 cos( 1 − 2) ≤ 2. (т.к. 0<=cos<=1).
В интеграле I2: ( ) = (1−2) − 1 непрерывна на ограниченном множестве |x| <= A. Тогда:

| ( |
) − ( )| = 2 ∫ |
( ) + ∫ |
| ( 1− 2) − 1| ( ) = 2 {| | > } + = |
|||
1 |
2 |
|
|
2 |
||
|
| |> |
| |≤ |
|
|
|
|
Тогда можно подобрать А таким, чтобы {| | > } < |
|
. Зафиксируем это А и в I2 при этом |
||||
4 |
||||||
|
|
|
|
|
||
фиксированном А в силу существования равномерной непрерывности : | 1 − 2| < => |
||||||||||
| | ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
+ |
|
∫| |≤ ( ) = |
|
+ |
|
{| | ≤ } ≤ ч. т. д. |
|
|
|
|
|
|
|||||
|
|
4 |
2 |
2 |
2 |
|||||
5. Вычисление моментов с использованием характеристической функции.
Если случ.вел. ξ имеет конечные моменты до n-ого порядка включительно ( |ξn| < +∞), то ее характ.ф-ция ξ( ) имеет n первых производных и ( )( ) = ξk 0 ≤ ≤ .
Док-во. По индукции k=1. По условию теоремы |ξ| = ∫−∞∞| | ( ) < +∞. Продифференцируем функцию ( ) = ∫−∞∞ ( ) по t: ′( ) = ∫−∞∞ ( ). По теореме о дифференцируемости под знаком интеграла необх. и дост., чтобы одна из функций была ограничена, а интеграл от модуля второй функции был конечен.
| | ≤ 1 и ∫−∞∞| | ( ) < +∞ => дифференцирование возможно и производная существует. Рассмотрим ее значение в 0: ′(0) = ∫−∞∞ ( ) = ξ.
6. |
|
Построить характеристическую функцию ξ~N(0,1). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) = |
|
1 |
|
|
|
− |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ξ0 |
|
|
|
√2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
ξ0( ) = ∫−∞∞ |
|
|
1 |
|
− |
|
= |
|
1 |
|
∫−∞∞ |
− |
( 2−2 +( )2−( )2) = |
|
1 |
∫−∞∞ |
− |
( − )2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
√ |
|
|
|
√ |
|
|
√ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( )2 |
|
|
|
− 2 |
|
|
∞ |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
−2 ( − ) |
( |
|
|
|
) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
= √ |
2 |
|
|
|
|
∫−∞ |
|
|
|
|
|
|
|
|
|
− |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=√2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вычисление первых двух моментов распределения: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
′ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
′ |
|
|
( ) = − |
|
|
|
(− |
|
|
|
) = − − |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
(0) = 0 = ξ => ξ = 0 |
|
|
|
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
ξ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ0 |
|
|
|
|
|
|
|
|
|
||||||||
|
′′ |
|
( ) = − |
− |
2 |
|
+ |
2 |
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
(0) = −1 = |
2 |
2 |
2 |
= 1 |
|||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ξ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ0 |
|
ξ |
=> ξ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. Пусть ξ – целочисленная случ.вел., xk = k .
Производящей функцией называется функция ( ) = ∑∞=1 , где z = a + ib : | | ≤ 1. Свойства производящей функции:
1)ξ1+ +ξn( ) = ξ1( ) … ξ ( ) для независимых случ.вел. ξ1, … , ξn
2)ξ = ′(1) ; ξ = ′′(1) + ′(1) − ( ′′(1))2
3){ξ = } = 1! ( )(0)
8. Теорема о разложении характеристической функции в ряд.
Если случ.вел. ξ имеет характ.ф-цию ( ), то ( ) может быть представлена в виде суммы:
( ) = ∑=0 |
( ) |
ξk |
+ ( ξk) (ряд Тейлора). |
|
! |
||||
|
|
|
9. Теорема о единственности характеристической функции.
Если F(x) и G(x) – функции распределения с одной и той же характеристической функцией ( ), т.е. ( ) = ∫−∞∞ ( ) = ∫−∞∞ ( ), то ф-ции распределения тождественно равны
{ξ < } = { < }.
10. Теорема Бохнера-Хинчина. Пусть . ( ) – некоторая ф-ция такая, что . (0) = 1. Для того, чтобы . ( ) была характ.ф-цией, необходимо и достаточно 1, … , , 1, … , существовала квадратурная формула:
∑ ∑ ( − ) ̅ ≥ 0
=1 =1
11. Теорема Пойа (признак характеристичности).
Пусть ( ) непрерывна, четная и выпуклая вниз функция такая, что (0) = 1, ( ) ≥ 0, ( ) → 0 при → ∞. Тогда ( ) – характеристическая функция некоторой случайной величины.
12. Теорема Марцинкевича.
Если характ.ф-ция имеет вид ( ) = ( ) , где ( ) = 0 + 1 −1 + +
(полином), то степень n не может быть больше 2.
13. Теорема Леви (о непрерывности).
Пусть { ( )}∞=1 - последовательность функций распределения. { ( )}∞=1 - последовательность соответствующих характ. ф-ций. Тогда:
|
|
|
|
|
( ) → ( ) |
( – слабая сходимость) |
||
1) |
если ( ) → ( ), то |
|||||||
|
|
|
|
|
|
|
|
|
2) |
если |
lim |
( ) и lim |
( ) = ( ), где ( ) непрерывна в t=0, то ( ) является |
||||
|
|
→∞ |
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
||
характ.ф-цией распределения ( ) |
|
|||||||
→ ( ). |
|
|||||||
|
|
|
|
|
|
|
|
|
2. Предельные теоремы и Законы больших чисел
1. ξ Говорят, что {ξi}∞=1 сходится по вероятности к случ.вел. ξ, если
→∞ |
→∞ |
|
|
> 0 {|ξn − ξ| ≤ E} → |
1 ( > 0 {|ξn − ξ| > E} → |
0) . |
ξn → ξ . Сходимость по |
вероятности означает, что при больших n практически невозможно наблюдать отклонения |
|||
больше, чем Е. |
|
|
|
Последовательность {ξi}∞=1 сходится почти наверное к случ.вел. ξ, если > |
|||
→∞ |
→∞ |
|
п.н. |
0 { : ξn( )¬→ ξ( )} → 0 |
или > 0 { : ξn( ) → ξ( )} → |
1. |
ξn → ξ |
Последовательность {ξi}∞=1 с |ξn| < +∞ сходится в среднем к случ.вел. ξ с |ξ| < +∞, если
lim |ξn − ξ| = 0. ξn → ξ
→∞
Последовательность {ξi}∞=1 сходится по распределению к случ.вел. ξ если во всех точках
непрерывности lim |
( ) = ( ). ξ |
|
|
||||
→ ξ |
|
||||||
|
→∞ |
|
|
n |
|
|
|
2. Теорема о сходимости по вероятности функции от случайной величины. |
|||||||
|
|
|
|
|
|
|
|
Если ξn → ξ, f(x) – непрерывная функция, то (ξn) → f(ξ). |
|
||||||
Док-во. Т.к. f(x) – непрерывная функция, то |
|
||||||
> 0 > 0: {| (ξn) − f(ξ)| ≥ |
|ξ| ≥ |ξn − ξ| ≥ } ≤ {|ξ| ≥ } + |
||||||
|
|
|
|
|
|
|
|
{|ξn − ξ| ≥ }, где {|ξn − ξ| ≥ } → 0, т.к. по условию ξn → ξ. |
|
||||||
{| (ξn) − f(ξ)| ≥ } ≤ lim {|ξ| ≥ } |
|
|
|||||
→ 0, следовательно (ξn) → f(ξ). |
|
||||||
|
|
|
→∞ |
|
|
||
3. Теорема о связи между сходимость в среднем, по вероятности, по распределению. |
|||||||
|
|
|
|
|
|||
ξn → ξ => ξn → ξ => ξn → ξ. |
|
|
|||||
Док-во: будем использовать неравенство Чебышева: > 0 {ξ ≥ 0} = 1 |
ξ < +∞: |
||||||
{ξ ≥ E} ≤ |
Mg(ξ) |
, где g(x) – непрерывно убывающая функция. |
|
||||
|
|
||||||
|
g(ξ) |
|
|
|
|
|
|
Следствие: {ξ < ξ} ≤ |
Dξ |
|
|
|
|||
2 |
|
|
|||||
|
|
|
|
E |
|
|
|
1) Из сходимости в среднем следует сходимость по вероятности. |
|
||||||
|
|
|
|
|
|
|
|
|
|
Т.к. ξn → ξ, то |ξn − ξ| → 0. Применим неравенство Чебышева к неотрицательной случ.вел. |
|||||||||
→∞ |
|
|
|
|
|
|
|
|
|
|ξn − ξ| с g(x)=x. Тогда > 0 |
{ξn ≥ ξ} ≤ |
M|ξn−ξ| |
|
|
|
||||
|
|
→ 0, т.е. по определению ξn → ξ. |
|||||||
ξ |
|||||||||
|
|
|
|
|
|
|
|||
2) Из сходимости по вероятности следует сходимость распределению. |
|||||||||
|
|
→∞ |
|
|
|
|
|
|
|
По условию > 0 {|ξn − ξ| |
> E} → 0. Сходимость по распределению означает, что ξn( ) |
||||||||
|
|
|
|
|
|
|
|
|
|
→ Fξ( ) в каждой точке непрерывности. Пусть 0 – точка непрерывности этой функции. |
|||||||||
Выберем x’, x’’: ′ < < ′′. Рассмотрим вероятность следующего события: |
|||||||||
0 |
|
|
|
|
|
|
|
|
|
(x′) = P{ξ < x′} = P{ξ < x′ ∩ ξ |
< } + P{ξ < x′ ∩ ξ |
≥ |
} ≤ P{ξ |
< } + |
|||||
ξ |
|
0 |
|
|
|
0 |
|
0 |
|
P{|ξn − ξ| ≥ 0 − ′}, где P{|ξn |
− ξ| ≥ 0 − ′} → 0 при фиксированном ξ = 0 − ′. |
||||||||

ξ(x′) = lim ξn(x0).
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
, ξ ≥ x′′ } ≤ P{ξ ≤ x′′} + |
|
|||||||||||||||
|
(x |
0 |
) |
= P{ξ |
< x |
0 |
} = P{ξ < x |
0 |
, ξ < x′′ } + P{ξ |
n |
< x |
0 |
|
|||||||||||||||||||||||
|
ξn |
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P{|ξ |
− ξ| ≥ x′′ − x |
0 |
}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
) ≤ (x′′). Таким образом (x′) |
|
|
|
|
|
|
|
|
|
|
) ≤ (x′′); т.к. – |
|||||||||||||||||||
|
lim |
|
(x |
0 |
≤ lim |
|
(x |
0 |
) ≤ lim |
(x |
0 |
|||||||||||||||||||||||||
→∞ |
ξn |
|
|
ξ |
|
|
|
|
|
|
|
ξ |
|
|
ξn |
|
|
→∞ |
ξn |
|
|
ξ |
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точка непрерывности, то lim ′ |
= , |
lim ′′ |
= . |
lim |
(x |
0 |
) = |
( ) |
. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
0 |
→∞ |
|
|
0 |
|
→∞ |
ξn |
|
|
ξ |
|
0 |
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Теорема о связи между сходимостью по вероятности и сходимостью к константе по распределению.
Если {ξi}∞=1 сходится по распределению к С (const), то ξ сходится к С и по вероятности. (Если
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ → С, то ξ → С). |
|
|
|
|
|
|
|
( ) = {1, > . lim |
|
|
|
|||||||
Док-во. Рассмотрим функцию распределения |
( ) = ( ) при ≠ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, ≤ →∞ |
ξn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рассмотрим {|ξ |
|
− C| |
< } = { − < ξ |
< C + E} ≥ { − |
|
< ξ |
|
< C + E} = |
||||||||||
n |
|
n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
( + ) − |
( − |
|
) → |
|
( + ) − |
( − |
|
) = 1 − 0 = 1. |
|
|
|
|
|||||
|
2 |
|
|
|
|
|||||||||||||
ξn |
|
ξn |
|
|
|
2 →∞ |
|
|
|
|
|
|
|
|
|
|||
Таким образом, > 0 {|ξn − C| < } → 1 => по вероятности ξ → С.
→∞
5. Говорят, что последовательность {ξi}=1∞ |
с ξ < +∞ удовлетворяет закону больших чисел, |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
если последовательность |
|
→ |
|
|
, где = ξ + + ξ , т.е. |
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
n |
||
|
|
|
|
|
|
|
|
||||
> 0 {| |
ξ1+ +ξn |
− |
Mξ1+ +Mξn |
| < } → 1 при → ∞. |
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
6. Теорема закон больших чисел (ЗБЧ) для независимых одинаково распределенных случайных величин.
Пусть {ξi}∞=1 - последовательность независимых одинаково распределенных случайных
|
|
|
|
|
|
|
= 2. Тогда |
|
|
|
|
|
|
|
|
|
||||||
величин с ξ |
|
= < +∞, ξ |
|
|
→ |
и |
{ξ } удовлетворяет ЗБЧ. |
|
|
|||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
+ +ξ |
n |
|
ξ |
1 |
|
|
|
ξ |
n |
|
|
|
|
|
|
||
Док-во. Рассмотрим |
|
= |
1 |
|
|
= |
|
+ + |
|
|
. Т.к. ξ |
|
одинаково распределены, то все ξ |
|
имеют |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
одну и ту же характеристическую функцию ξ1( ) = = ξ ( ). Рассмотрим ξ1( ). Получим
ξ1( ) = ξ1 ( ) (по свойству ( ) = + ξ( )).
По теореме о разложении характ. ф-ции в ряд получим: 1 + 1!1 ( ) ξ1 + ( ) ξ1 = 1 + +
( |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим характ. ф-цию ( ) = ( ξ |
( )) |
= ( |
( |
)) |
= (1 + |
+ ( |
)) |
→ = |
|||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
ξ1 |
|
|
|
|
|
|
→∞ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( ). |
|
→ 0 |
|
( ) = = . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
То теореме о непрерывности (Леви) из доказанной сходимости ( ) → |
|
( ) следует |
|||||||||
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) → ( ). |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом |
|
→ => |
|
→ . |
|
|
|
||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
7. Центральная предельная теорема.
Пусть {ξi}∞=1- последовательность независимых одинаково распределенных случайных
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
∞ |
|
|
|
(− |
2 |
) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
величин с ξ |
= < +∞, ξ |
|
|
{ |
|
|
|
|
|
|
|
|
|
< } → |
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
2 |
|
|
. Если |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
→∞ √ |
2 |
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
|
|
|
, то |
→ ξ ~ (0,1). (Смысл – суммарное воздействие многих факторов становит |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
√ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
нормальным). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
(ξ |
− )+ +(ξ |
|
− ) |
|
|
|
|
ξ |
− |
|
|
|
|
|
ξ |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Док-во. Рассмотрим случ.вел. |
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
+. . . + |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
√ ξ |
+ + ξ |
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим случ.вел. (ξ |
|
− ). Ее (ξ |
|
− ) = 0, где (ξ |
|
|
− ) |
|
= (ξ ) |
|
= 2 = (ξ |
|
− )2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
Пусть ξ1−( ) – характ.ф-ция случ.вел. (ξ1 − ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
ξ1− ( ) = ξ1− ( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
(ξ − )2 + ( |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= 1 + |
|
|
|
|
( |
|
|
|
|
|
|
|
|
) (ξ |
− ) + |
|
( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
) (ξ − ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1! √ |
1 |
|
|
|
|
|
|
|
|
|
2! √ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= 1 − |
|
|
|
2 |
|
|
2 |
+ |
( |
|
2 |
) = 1 − |
|
|
2 |
|
+ |
( |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Построим характ.ф-цию − = ( ξ |
|
−( )) |
= |
|
(1 − |
2 |
|
+ ( |
2 |
)) |
|
→ |
|
|
|
|
|
− |
|
|
|
= |
|
|
( ), где |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
ξ0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ξ0~ (0,1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, по теореме о непрерывности (Леви) из данной сходимости − |
→ |
|
|
ξ0 |
( ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
следует слабая сходимость ф-ций распределения |
|
( ) |
→ ( ), |
|
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
→ ξ ~ (0,1). |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Математическая статистика
Вариационные ряды и их характеристики. Генеральная и выборочная совокупности, объём выборки, вариационный ряд, варианта, частота. Виды вариационных рядов. Гистограмма, полигон. Формулы числовых характеристик. Эмпирическая функция распределения(ЭФР). Свойства ЭФР.
Задача
По результатам наблюдения за некоторой случайной величиной ξ требуется сделать выводы о неизвестном законе распределения этой величины L(x,θ) либо о неизвестных параметрах
θ1,…,θn
известного распределения.
Пусть ξ --- случайная величина с некоторой теоретической функцией распределения Fξ ( x)= P{ξ< x},x R .
Совокупность n независимых одинаково распределенных случайных величин
X1, X2, … , Xn
называется выборкой, извлеченной из распределения случайной величины ξ.
Набор n значений x1, x2 ,…, xn
случайных величин
X1,X2 ,…, Xn
называется реализацией выборки или выборкой из генеральной совокупности значений случайной величины ξ.
Под генеральной совокупностью понимается множество всех возможных значений случайной величины ξ.
Объем совокупности есть количество всех ее элементов, объем выборки или выборочной совокупности обозначается n, генеральной совокупности — N.
Выборочным пространством называется множество Xn всех возможных выборок объема n, извлеченных из распределения L(x,θ) случайной величины ξ.
Вариационные ряды, гистограмма, полигон частот

Вариационным рядом называется последовательность расположенных в порядке неубывания элементов выборки
x*1≤ x*2≤,…,≤x*n .
Элементы вариационного ряда называются вариантами.
Точечным вариационным рядом называется таблица вида
xi |
x1 |
x2 |
… |
xm |
ni |
n1 |
n2 |
… |
nm |
|
|
|
|
|
Где xi ---варианты, ni ---частоты, m --- количество групп,
Для графического представления точечных вариационных рядов используется полигон частот---ломаная с вершинами в точках (xi ,ni).
Интервальным вариационным рядом называется таблица вида
xi |
[x1,x2] |
(x2,x3] |
… |
(xm,xm+1] |
|
|
|
|
|
ni |
n1 |
n2 |
… |
nm |
|
|
|
|
|
Где xi --- варианты,ni --- частоты,m --- количество групп (интервалов),
Для графического представления интервальных вариационных рядов используется гистограмма частот --- фигура, составленная из прямоугольников, одной стороной которых служат интервалы(xi, xi+1], а длина второй равна ni.
Объем выборки и в том и в другом случае равен:
m
n=∑ ni
i=1
Числовые характеристики вариационных рядов
Пусть X1,X2,…,Xn L(x,θ) --- выборка из распределения сл.в. ξ.
Выборочным средним называется величина
Если данные представлены в виде точечного или интервального вариационного ряда, то для вычисления используют формулу:
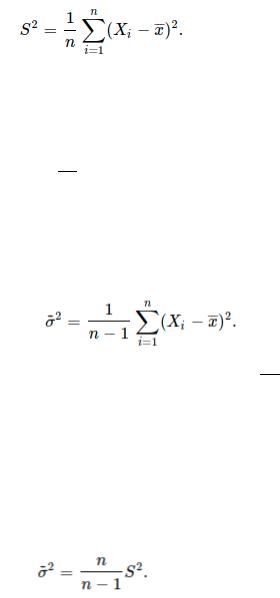
где m – количество групп в точечном или интервалов в интервальном вариационном ряду, ni – частота, т.е. количество элементов выборки, принадлежащих j - той группе или j - тому интервалу, xj – варианта для точечного ряда и середина j - того интервала для интервального ряда.
Выборочной смещенной дисперсией (неисправленной) называется величина
Она характеризует среднее из квадратов отклонений наблюдаемой величины от выборочного среднего. Величина
S=√S2 называется выборочным средним квадратическим отклонением (смещенным) величин выборки от выборочного среднего.
Выборочной несмещенной дисперсией (исправленной) называется величина
~ |
~2 |
называется выборочным несмещенным |
Аналогично, величина σ =√σ |
||
средним квадратическим отклонением.
Очевидно, что смещенная и несмещенная выборочные дисперсии связаны формулой
~ |
~ |
Кроме того, при любом n σ2≥S2 |
,a lim S2=σ2 |
|
n→∞ |
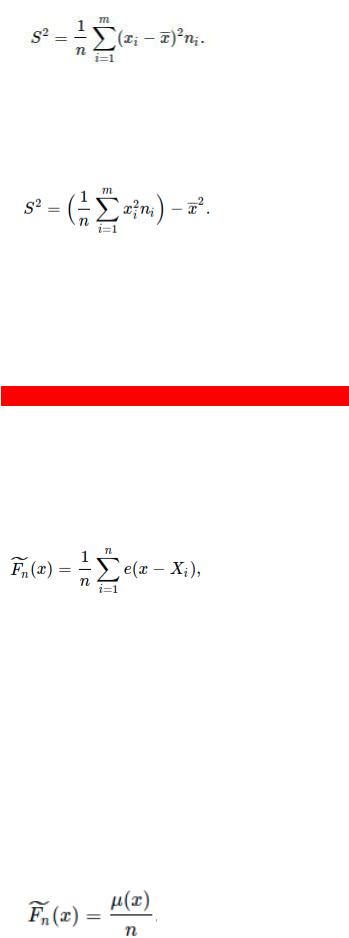
Если данные представлены в виде точечного или интервального вариационного ряда, то для вычисления используют формулу:
или
Здесь m – количество групп в точечном или интервалов в интервальном вариационных рядах,ni – частота, т.е. количество элементов выборки, принадлежащих i --той группе или i--тому интервалу, xi -- варианта для точечного ряда и середина i--того интервала для интервального ряда
Эмпирическая функция распределения
Пусть X1, X2 ,…, Xn выборка из распределения сл.в. ξ с теоретической функцией распределения Fξ(x).
Определение. Эмпирической функцией распределения (ЭФР) называется функция
где e(x)=1, при x>0, e(x)=0, при x<=0.
Таким образом, если Xi < x, то e(x) = 1, если Xi x, то e(x) = 0, а сумма e(x−Xi) будет равна количеству элементов выборки, которые приняли значение, строго меньше некоторого x R.
Пусть x1, x2 ,…, xn - реализация выборки X1, X2, …, Xn, т.е. наблюдавшиеся значения сл.в. ξ. Обозначим μ(x) - число элементов выборки, строго меньших x R.
Тогда эмпирическая функция распределения ~n ( )
F x может быть
определена как
