
- •17. Пространство Rm . Последовательности в Rm и их свойства.
- •19. Теорема о непрерывном образе линейно связного множества и ее следствия.
- •22. Т. Достаточное условие дифференцируемости.
- •25. Частные производные высшего порядка. Теорема о равенстве смешанных производных. Непрерывно дифференцируемые и k-непрерывно дифференцируемые функции. Дифференциалы первого и высших порядков.
- •26. Т. Формула Тейлора с остаточным членом в форме Лагранжа.
- •27. Локальный экстремум функции многих переменных. Необходимое условие локального экстремума. Достаточное условие локального экстремума.
- •35. Собственные интегралы, зависящие от параметра. Теоремы о непрерывности, о дифференцировании и об интегрировании интеграла по параметру.
19. Теорема о непрерывном образе линейно связного множества и ее следствия.
Т. о непрерывном образе линейно связного мн-ва. Пусть функция непрерывна на множестве Х и множество Х –линейно связно. Тогда множество тоже линейно связно.
Следствие. Пусть функция f: X->R определена и непрерывна на линейно связном мн-ве Х ∈ Rm и принимает на нем значение А и В. Тогда эта функция принимает любое значение на промежутке между А и В.
20. Частные производные функции многих переменных. Дифференцируемость в точке функции многих переменных. Теорема о непрерывности дифференцируемой функции. Теорема о существовании частных производных у дифференцируемой функции.
Частной
производной
функции f
по первой переменной в точке
 называют предел
называют предел

Если
он существует, и обозначают
 или
или
 или D1
или D1 ,
,
Пусть точка является внутренней точкой области определения функции f. Функция f называется дифференцируемой в точке , если приращение функции в этой точке можно представить в виде:
 ,
где функции
,
где функции
 непрерывны в точке
.
непрерывны в точке
.
Т. о непрерывности дифференцируемой функции. Если функция f дифференцируема в точке , то она непрерывна в этой точке.
Т.
о существовании частных производных
у дифференцируемой функции.
Если функция f
дифференцируема в точке
,
то в этой точке в нее существуют все
частные производные при всех k=1,…,m
 ,
где
,
где

Док-во. По условию дифференцируемости функции в точке имеем
 .
Поделим
обе части равенства на
.
Поделим
обе части равенства на
 и перейдем к пределу при
и перейдем к пределу при
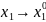 .
.
 . Аналогично для частных производных
по остальным переменным.
. Аналогично для частных производных
по остальным переменным.
21. Геометрический смысл условия дифференцируемости функции двух переменных. Касательная плоскость и вектор нормали к графику дифференцируемой функции.

Плоскость
с уравнением
 называется касательной
плоскостью
к графику функции z
= f(x,y)
в точке
называется касательной
плоскостью
к графику функции z
= f(x,y)
в точке

Записывая
уравнение касательной плоскости в
каноническом виде получается, что
вектор ( является нормальным вектором касательной
плоскости. Его называют нормальным к
графику функции в точке
является нормальным вектором касательной
плоскости. Его называют нормальным к
графику функции в точке
 .
.
22. Т. Достаточное условие дифференцируемости.
Если у функции f в некоторой окрестности точки существуют все частные производные и они непрерывны в ,, то функция f дифференцируема в точке .
Док-во.
Проведем док-во для функции двух переменных f(x,y) и точки (x0,y0).
Представим
приращение функции f:
 .
.
Выражение
в первой скобке можно рассматривать
как приращение функции
 одной переменной x
на [
одной переменной x
на [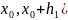 .
Применяя формулу Лагранжа, найдем
.
Применяя формулу Лагранжа, найдем
 такое, что
такое, что
 .
.
Т.к.
производная
 непрерывна в точке
непрерывна в точке
 ,
то
,
то
 ,
где
,
где
 – бесконечно малая функция при (
– бесконечно малая функция при ( .
.
Аналогично для второй скобки.
Таким
образом,
 .
Последнее равенство – условие
дифференцируемости функции f
в точке (
.
Последнее равенство – условие
дифференцируемости функции f
в точке ( ).
).
23. Т. о дифференцирование сложной функции.
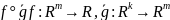 .
.

Пусть
функция f
дифференциуема в точке
,
функции
 при
всех i=1,…,m
дифференцируемы в точке
при
всех i=1,…,m
дифференцируемы в точке
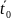 и
и
 .
Тогда композиция функций f
и
.
Тогда композиция функций f
и
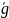 дифференцируема
в точке
и при любом j=1,…,k
верно
дифференцируема
в точке
и при любом j=1,…,k
верно

Док-во.
Т.к.
функция f
дифференцируема в точке
,
то
 ,
где функции
,
где функции
 непрерывны в точке
при i=1,…,m.
непрерывны в точке
при i=1,…,m.
Поскольку
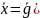 и
, то
и
, то

Т.к.
функции
дифференцируемы в точке
при всех i=1,…,m,
то найдутся непрерывные в точке
функции
 такие, что
такие, что
 и
и
 Тогда
Тогда
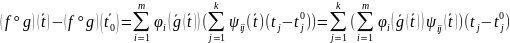
Последнее
равенство означает условие
дифференцируемости функции
 вточке
.
И при всех j=1,…,k
вточке
.
И при всех j=1,…,k

24. Производная по направлению и вектор градиент. Свойства вектора градиента.

Можно
расписать подробнее:
 .
.
Т.
Если функция f
дифференцируема в точке
,
то для любого единичного вектора
 существует производная функции f
в точке
по направлению вектора
существует производная функции f
в точке
по направлению вектора
 и верно равенство
и верно равенство
 .
.
Док-во. следует из теоремы о дифференцировании сложной функции.
Градиентом дифференцируемой в точке функции f называют вектор
 .
.
Св-ва вектор градиента:
1)
вектор градиент
 указывает направление, по которому
функция f
имеет максимальную производную в
точке
.
указывает направление, по которому
функция f
имеет максимальную производную в
точке
.
2)
значение производной функции f
по направлению, определенному градиентом
этой функции в точке
,
равно длине вектора градиента

