56. Диффиринциал функции

Определение: Функция f(x) называется дифференцируемой в точке , если её приращение в этой точке можно представить в виде (1), где А-const. - линейно относительно и отличается от приращения функции на бесконечно малую величину ; поэтому - главная линейная часть приращения функции.

Определение: Если функция f(x) дифференцируема в точке , то главную линейную часть её приращения называют дифференциалом функции в точке , с приращением ; обозначается: . dy=

Теорема: Утверждение, что f(x) дифференцируема в точке утверждению, что конечная , причем в 1 в роли A.Доказательство: :Итак, функция дифференцируема выполнено 1. доказано.

Доказательство: : Пусть конечная , докажем тогда по формуле для полного приращения функции , где 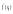- конечная, - . Сравнивая с 1, видим, что функция дифференцируема, причем 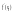=А доказано.

Замечание: Так как дифференцируемость конечная 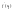, часто вместо дифференцируемость говорят производная, поэтому процесс нахождения производной называют дифференцированием. - дифференциал, и обозначается , поэтому с учетом теоремы:

Замечание2: Из

57. Градиент, производная по направлению

производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления: где — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора

58. Экстремум функции многих переменных (необходимое и достаточное условия).

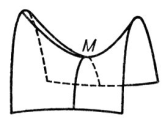
Экстремум (от лат. extremum - крайнее), значение непрерывной функции f (x), являющееся или максимумом, или минимумом. Точнее: непрерывная в точке х₀ функция f (x) имеет в x₀ максимум (минимум), если существует окрестность (x₀ + d, x₀ - d) этой точки, содержащаяся в области определения f (x), и такая, что во всех точках этой окрестности выполняется неравенство f (x₀), ³ f (x) [соответственно, f (x₀) £ f (x)]. Если при этом существует такая окрестность, что в ней f (x₀) > f (x) [или f (x₀) << f (x)] при х ¹ x₀, то говорят о строгом, или собственном, максимуме (минимуме), в противном случае - о нестрогом, или несобственном, максимуме (минимуме) (на рис. 1 в точке А достигается строгий максимум, в точке В - нестрогий минимум). Точки максимума и минимума называются точками экстремума. Для того чтобы функция f (x) имела Экстремум в некоторой точке x₀, необходимо, чтобы она была непрерывна в x₀ и чтобы либо f`(x<sub>0</sub>) = 0 (точка А на рис. 1), либо f`(x₀) не существовала (точка С на рис. 1). Если при этом в некоторой окрестности точки x₀ производная f"(x) слева от x₀ положительна, а справа отрицательна, то f (x) имеет в x₀ максимум; если f"(x) слева от x₀ отрицательна, а справа положительна, то - минимум (первое достаточное условие Экстремум). Если же f"(x) не меняет знака при переходе через точку x₀, то функция f (x) не имеет Экстремум в точке x₀ (точки D, Е и F на рис. 1). Если f (x) в точке x₀ имеет п последовательных производных, причём f"(x₀) = f``(x₀) =...= f ^(n-1) (x₀)=0, a f ⁽ⁿ⁾(x₀)¹0, то при п нечётном f (x) не имеет Экстремум в точке x₀, а при п чётном имеет минимум, если f ⁽ⁿ⁾ (x₀) > 0, и максимум, если f ⁽ⁿ⁾ (x₀) < 0. Экстремум функции не следует смешивать с наибольшим и наименьшим значениями функции. Аналогично Экстремум функции одного переменного определяется Экстремум функции нескольких переменных. Необходимым условием Экстремум является в этом случае обращение в нуль или же несуществование частных производных первого порядка. Например, на рис. 2 частные производные равны нулю в точке М, на рис. 3 в точке М они не существуют. Если в некоторой окрестности точки М (х₀, y₀) существуют и непрерывны первые и вторые частные производные функции f (x, у) и в самой точке f"_x = f"_y = 0, D = f"" _xx f"" _уу > 0, то f (x, у) в точке М имеет Экстремум (максимум при f""_xx < 0 и минимум при f""_xx > 0); Экстремум в точке М не существует, если D < 0 (в этом случае М является т. н. седловиной, или точкой минимакса, см. рис. 4). Достаточные условия Экстремум функций многих переменных сводятся к положительной (или отрицательной) определённости квадратичной формы Sⁿ_{i, k=1} a_ikDx_iDx_k где a_ik - значение f""x_ix_k в исследуемой точке.