Учебное пособие 800519

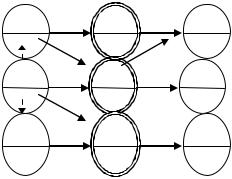
рукописями, для которых i ≤ 0 в очередности убывания qi. Заметим, что с параметрами i, qi задаче можно дать другую экономическую интерпретацию.

Задача самоокупаемости. Имеется n проектов. Проект i требует финансирования qi, а после реализации дает доход i (или убыток, если i – отрицательно, что имеет место для социальных проектов). Предполагается, что проекты реализуются поочередно. Для реализации всех проектов берется кредит S. Задача заключается в определении очередности реализации проектов, при которой требуется минимальный кредит. В такой интерпретации правило определения оптимальной очередности выглядит достаточно естественным. Действительно, вначале целесообразно выполнять проекты, дающие положительный (неотрицательный) доход, начиная с тех, которые требуют минимального финансирования, а затем – убыточные проекты, начиная с самых дорогих.

Применим это правило для решения задачи устранения «узких мест» в более общем случае. Рассмотрим сетевой график на рис. 9.2.3.

Рис. 9.2.3

Работы 4, 5 и 6, как и в задаче редактора, образуют «узкое место» сетевого графика, поскольку выполняются ресурсами других видов, количество которых достаточно. Работы 1, 2, 3, 7, 8 и 9 выполняются единицей ресурсов. Отличие от задачи редактора в том, что существуют дополнительные зависимости между работами (это зависимости (1,5), (2,6) и (5,7)).

Разделим работы, выполняемые ресурсами первого вида, которые связаны зависимостями с несколькими работами, образующими «узкое место», на несколько отдельных работ (по числу зависимостей). При этом продолжительность работы делим произвольным образом между работами, на которые разделена данная работа. Так, работу 1 делим на две работы, продолжительности которых равны 2 и 1 соответственно. Работу 2 делим на две работы, продолжительности которых равны 3 и 3 соответственно. Наконец, работу 7 делим на две работы, продолжительности которых равны 1 и 2 соответственно. Теперь суммируем продолжительности работ, предшествующих одной и той же работе «узкого места». Соответственно суммируем продолжительности всех работ, следующих за одной и той же работой «узкого места». В результате получаем задачу редактора (рис. 9.2.4).

231

позже работы 3, то есть мы можем начать работу 6 раньше работы 5. Дело в том, что решение задачи редактора получено при условии, что очередность первичной обработки рукописей та же самая, что и очередность вторичной обработки. Если это условие отбросить, то полученное правило определения очередности обработки рукописей может не дать оптимального решения. Так, если 0 ≤ x1 <2, то при очередности обработки II I работа 3 заканчивается в момент времени t3 = 22, что меньше, чем момент окончания работы 4, t4 = 24-x1. Поэтому после окончания работы 3 начинается работа 5, а затем работа 6. Продолжительность обработки рукописей составит = 37 при любых 2 ≤ x1 ≤ 7

значение. Для решения этой задачи рассмотрим три случая. А. x1 + x2 ≤ 8. В этом случае

= min(38-x2; 39-x1) при x1 ≥ 2 и

= min(38-x2; 37)при 0 ≤ x1 ≤ 2.

Оптимальные значения: 0 ≤ x1 ≤ 2, 0 ≤ x2 ≤ 1, = 37. Б. 8 ≤ x1 + x2 ≤ 11. В этом случае

= min(30+x1; 39-x1).

Оптимальные значения: x1 = 4,5, 0 ≤ x2 ≤ 6,5, = 34,5. В. x1 + x2 ≥ 11. В этом случае

= min(30+x1; 28+x2).

Оптимальные значения: x1 = 7, x2 = 9, = 37.

Выбираем варианты А и В, дающие наибольшее значение нижней оценки. Для этих вариантов, как легко убедиться, оптимальная очередность обработки рукописей II I с продолжительностью обработки T = 37.

Возвращаясь к исходной задаче, определим продолжительность проекта при очередности работ 2 1. Она, как легко убедиться, равна T = 37, что совпадает с нижней оценкой. Поэтому полученное решение является оптимальным.

Получим достаточные условия, при выполнении которых в оптимальном решении задачи редактора очередности первичной и вторичной обработки рукописей совпадают. Пусть i1, i2, … , in – произвольная очередность первичной

234

обработки рукописей. Для того, чтобы вторичная обработка могла проводиться в той же очередности, достаточно выполнение следующих условий:

Эти условия эквивалентны следующим:

aik 1 bik 1 bik , k 1,n 1.

Для того, чтобы эти условия выполнялись для любой очередности, достаточно, чтобы для любых i, j имело место:

qi = ai + bi ≥ bj. (9.2.5)

При выполнении условия (9.2.5) приведенное выше правило определения очередности обработки рукописей в задаче о редакторе всегда будет давать оптимальное решение.

9.3. Распределение ресурсов по минимальной продолжительности работ

Проведем анализ второго правила приоритета работ, согласно которому максимальный приоритет имеют работы с минимальной продолжительностью. Рассмотрим сначала частный случай, когда это правило всегда дает оптимальное решение.

Задача Джонсона. Имеются n деталей, которые проходят обработку на двух станках. Обозначим через ai (bi) продолжительность обработки i-й детали на первом (втором) станке. Имеется по одному станку каждого типа. Требуется определить очередность обработки деталей на станках, минимизирующую продолжительность обработки всех деталей. Сначала обрабатываются детали, для которых ai ≤ bi в очередности возрастания ai. Затем обрабатываются детали, для которых ai ≥ bi в очередности убывания bi.

Заметим, что если для всех деталей имеет место ai ≤ bi, то оптимальным становится правило 9.1.2 упорядочения работ по возрастанию продолжительностей. Обоснование этого правила состоит в том, что если B bi ai A , то есть объем работ второго вида больше, чем объем работ

первого вида, то следует максимально быстро обеспечить фронт работ для ресурсов второго вида (в данном случае – для второго станка).

Дадим обобщение правила 9.1.2 на случай произвольного сетевого графика. Обозначим через Lj минимальное время, через которое можно начать хотя бы одну работу j-го вида, Rj – минимальное время завершения проекта после выполнения всех работ j-го вида, j, как было определено выше, – минимальная продолжительность выполнения всех работ j-го вида, Tкр – длина критического пути (минимальная продолжительность проекта при наличии достаточного количества ресурсов). Заметим, что величина

Mj = Lj + j + Rj

является оценкой снизу продолжительности проекта. Обозначим через

M max Mj Mk .

j

235

Если Mk >> Tкр, то очевидно, что следует обратить первоочередное внимание на выполнение работ k-го вида, а следовательно, приоритет получают работы, выполнение которых позволяет максимально быстро открыть фронт для работ k-го вида.

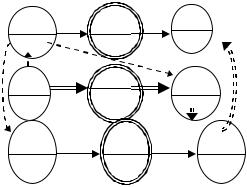
Рассмотрим сетевой график на рис. 9.3.1.

Рис. 9.3.1

Все работы выполняются единицей ресурса. Продолжительности работ указаны в нижних половинах кружков. Работы, выполняемые ресурсами второго вида, выделены. Имеется по единице ресурсов каждого вида. Вычисляем Tкр= 52. Определяем L2. Чтобы начать работу 5, необходимо выполнить работы 1, 2 и 4, что требует 17 дней. Чтобы начать работу 8, необходимо выполнить работы 3 и 6, что требует 14 дней. Следовательно, L2 = 14. После завершения всех работ второго вида потребуется минимум R2 = 5 дней для завершения проекта. Суммарная продолжительность работ второго вида равна 2 = 51. Имеем:

М2 = 14 + 51 +5 = 70 >> 52.

Следовательно, скорейшее начало выполнения работ второго вида является приоритетной задачей.

1 шаг. t = 0. Выполняем последовательно работы 3 и 6, максимально быстро открывающие фронт работ для ресурсов второго вида.

2 шаг. t = 14. Выполняем работу 8 и последовательно работы 9, 1, 2 и 4. 3 шаг. t = 28. Выполняем работу 12 и последовательно работы 4, 10 и 13. 4 шаг. t = 44. Выполняем последовательно работы 5, 7 и 11.

Продолжительность проекта составляет T = 70 дней, что совпадает с нижней оценкой. Таким образом, полученное обобщение правила приоритета по минимальным продолжительностям можно сформулировать в следующем виде:

Правило 9.3.1. В первую очередь начинаются работы, выполнение которых за минимальное время открывает фронт работ для определяющих

ресурсов (то есть ресурсов k-го вида, таких, что k = max j > Tкр).

j

236

9.4. Распределение ресурсов по минимальным поздним моментам окончания

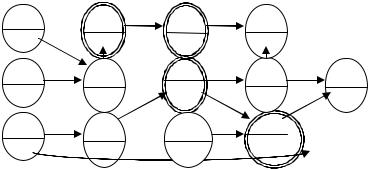
Будем рассматривать задачи распределения ресурсов в следующей постановке. Существует фронт работ, разделяющий сетевой график на две части. Работы левой части выполняются единицей ресурсов первого вида, каждая работа правой части выполняется ресурсами других видов, количество которых достаточно для выполнения всех работ за минимальное время. Количество ресурсов первого вида равно 1.

Обозначим через R множество начальных работ других видов, то есть таких работ, которые могут выполняться сразу после выполнения работ первого вида. Далее обозначим через Ai – множество работ первого вида, предшествующих работе i R (множество работ Ai необходимо выполнить для того, чтобы можно было выполнить работу i). Наконец, обозначим через

(Ai) j .

j A i

Утверждение 9.4.1. Существует оптимальное решение, в котором работы

Доказательство. Пусть определено расписание работ, в котором работы множества R начинаются в определенной очередности:

также не увеличились. Продолжая таким образом, получаем расписание, в котором работы выполняются в очередности (9.4.1), а продолжительность

проекта T не увеличилась. Обозначим через Tio поздний момент окончания всех работ множества Аi (эта же величина определяет поздний момент начала работы i R).

Теорема 9.4.1. Правило выполнения множества работ Ai в очередности

возрастания поздних моментов окончания Tio дает оптимальное расписание проекта.

Доказательство. Пусть = (i1,i2,…,in) – оптимальное расписание (то есть оптимальная очередность выполнения работ множества Ai) и пусть k –

множеств работ Ai k и Ai k 1 . Заметим, что это никак не повлияет на моменты

начала остальных работ i R. Обозначим через ti моменты начала работ i R в расписании , T0 – минимальная продолжительность проекта, Tкр – продолжительность проекта при наличии достаточного количества ресурсов всех видов. Имеем

продолжительность проекта по-прежнему равна T0. Продолжая таким образом, получаем оптимальное решение, в котором все работы множества Ai выполняются в очередности убывания поздних моментов окончания Теорема доказана.

Рассмотренный частный случай определяет ситуации, в которых предпочтительно применять правило 9.1.3 в его модифицированной форме. Эти ситуации можно охарактеризовать следующим образом. Имеется множество работ A Ai , выполняемых ограниченным количеством ресурсов одного вида

i

(левая часть сетевого графика), для которых необходимо определить приоритетность выполнения. Имеется второе множество работ, выполняемых ресурсами других видов (правая часть сетевого графика), количество которых достаточно для выполнения каждой работы за минимальное время. Суть правила сводится к тому, чтобы возможно скорее начать работы второго множества с минимальными поздними сроками начала, что соответствует приоритету работ множеств Ai с минимальными поздними моментами окончания Tio .

238

9.5. Гибкие правила приоритета работ

Проведенный анализ эвристических правил приоритета показал, что нет универсального эффективного правила. Различные правила эффективны в различных ситуациях, причем ситуация может измениться в процессе реализации проекта. Поэтому наиболее эффективной является гибкая система приоритетов. Суть ее в том, что по мере реализации проекта следует анализировать тип складывающейся ситуации и в зависимости от нее применять то или иное правило приоритета. В простейшем случае для выбора правил приоритета можно воспользоваться введенными ранее характеристиками: Ткр и Tj, . Напомним, что Ткр – это продолжительность проекта при условии, что продолжительности всех работ равны минимальным, Tj – это минимальное время, требуемое для выполнения всех работ j-го вида. Если

max Tj Tk Tкр, Tk Tj , j k ,

j

то это значит, что ресурсы k-го вида являются определяющими и следует применить модификацию правила 9.1.2, то есть максимально быстро открыть

фронт работ для k-го вида ресурса. Если Tкр max Tj , то следует предпочесть

j

правило 9.1.1 (по степени критичности работ), обращая особое внимание на

возможность появления узких мест. Если max Tj Tk Tкр , причем работы k-го

j

вида выполняются и в начальной стадии проекта, и в его завершающей стации, то можно построить оценочную задачу редактора и определить правила

приоритета работ на этой основе. Наконец, если max Tj Tk Tкр , причем работы

j

k-го вида выполняются в начальной стадии проекта, а затем выполняются работы других видов, обеспеченные ресурсами в достаточной степени, то целесообразно применение изложенной выше модификации правила 9.1.3.

Заметим, что если оценка Tкр и {Tj} различаются незначительно, то можно не менять применяемого правила, поскольку в такой ситуации все правила, как показывают примеры расчетов, дают близкие результаты. Из сказанного следует, что пересчет оценок Tкр и {Tj} следует осуществлять периодически.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Сформулируйте общую постановку задачи распределения ресурсов.

2.В чем заключается правило распределения ресурсов по степени критичности работ?

3.В чем заключается правило распределения ресурсов по минимальной продолжительности работ?

4.Сформулируйте понятие пропускной способности фронта работ F.

5.Какие сетевые графики называются монотонными?

6.В чем заключается задача редактора?

7.Сформулируйте общую постановку задачи самоокупаемости.

239

8.В чем заключается правило распределения ресурсов по минимальной продолжительности работ?

9.Сформулируйте общую постановку задачи Джонсона.

10.В чем состоит эффективность гибких правил приоритета работ?

ГЛАВА 10. МОДЕЛИ И МЕХАНИЗМЫ МАТЕРИАЛЬНОТЕХНИЧЕСКОГО ОБЕСПЕЧЕНИЯ В ЗАДАЧАХ УПРАВЛЕНИЯ

10.1. Определение согласованных цен на материалы и оптимальное распределение заказов

В централизованной схеме снабжения вопросы материальнотехнического обеспечения берет на себя специализированная организация (центр), заключающая договор с организациями-потребителями. Центр проводит оптовые закупки продукции у производителей, что позволяет ему покупать по более низким ценам и за счет этого обеспечивать привлекательность централизованной схемы для потребителей.

Рассмотрим сначала задачу снабжения одним видом продукции. Пусть в регионе имеется n организаций – потенциальных потребителей продукции данного вида. Обозначим через ci цену, по которой i-й потребитель согласен приобретать продукцию у центра, а через vi – количество продукции, требуемое i-му потребителю в рассматриваемый период времени. Очевидно, что потребитель i будет выбирать централизованную схему снабжения, если цена продукции у центра, которую мы будем обозначать через q, будет меньше или равна ci, то есть q ci. Таким образом, количество продукции, которое будет заказано центру, равно сумме потребностей тех потребителей, для которых централизованная схема является выгодной.

Обозначим через P(q) множество потребителей, выбирающих централизованную схему снабжения при цене продукции центра равной q. Тогда количество продукции, заказываемое у центра, можно записать в следующем виде:

i P(q)

Зависимость V(q) имеет вид, показанный на рис. 10.1.1. Это кусочнопостоянная, непрерывная слева, убывающая функция q.

V(q)

v1

v2

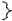v3

Рис. 10.1.1

240