Учебное пособие 800519

Дадим модификацию рассмотренного механизма на наш случай. Решение задачи (8.7.1), (8.7.2) в нашем случае – это метод «затраты-эффект», который уже рассматривался в раннее. Пусть все проекты упорядочены по эффективности и (k+1) – последний проект, получивший финансирование Sk+1 от корпоративного центра.

Примем ставку внутреннего кредита равной следующей величине:

= Эk+1 – ρ0, (8.7.7)

где Эk+1 – эффективность (k+1)-го проекта, ρ0 – минимальная рентабельность, при которой проекты предприятий принимаются к рассмотрению корпоративным центром. Проведем исследование проблемы манипулирования информацией для предложенного механизма. Заметим, во-первых, что оценки первых k проектов не влияют на ставку β. Поэтому для соответствующих предприятий имеет место обычный конкурсный механизм на основе метода «затраты-эффект». Рассмотрим предприятие (k+1). Для этого предприятия прибыль равна

то есть прибыль растет с ростом оценки Sk+1. Следовательно, в отличие от классического случая, манипулирование информацией имеет место, как и в конкурсном механизме. Однако в данном случае имеются новые варианты манипулирования информацией для первых k проектов, направленные на уменьшение β. Рассмотрим эти варианты на примере.

Пример 8.7.1. Имеются три проекта, данные о которых приведены в табл. 8.7.1, причем первый и второй проект представлены первым предприятием, а третий – вторым.

Таблица 8.7.1

Пусть R = 70, ρ0 = 0,2, μ = 0,8, = 0,2.

Если все предприятия сообщили истинные оценки, то финансирование получают первые два проекта. При этом, ставка внутреннего кредита= Э2 - 0 = 0,8 и прибыль первого предприятия составит

П1 = 0,8 (100 – 36) + 0,8 (80 – 72) = 57,6.

А. Если первое предприятие завысит оценку по первому проекту до 30, то его прибыль составит

П1 = 1,2 · 10 + 0,8 (100 – 54) + (80 – 72) = 55, 2 < 57,

то есть прибыль уменьшилась. Это и понятно, так как

μ + β = 1,6 > 1 + = 1,2

Б. Возьмем другой вариант. Первое предприятие завышает на 10 оценку по второму проекту. В этом случае ставка внутреннего кредита составит

222

β = Э2 – 0,2 = 0,6 – 0,2 = 0,4,

и прибыль первого предприятия П1 = 1,2 + 0,8 (100 – 28) + 0,8(80 – 70) = 77,6,

что существенно превышает 57,6.

Эти два способа манипулирования достаточно очевидны. Однако возможны нестандартные способы манипулирования, направленные на уменьшение ставки β. Рассмотрим эти способы.

В. Пусть первое предприятие сообщило оценку S2 = 60 по второму проекту. В этом случае средств на финансирование второго проекта не хватает, и финансирование получает третий проект второго предприятия. Ставка внутреннего кредита становится равной β= Э3 – 0,2 = 0 и прибыль первого предприятия составит

Г. Однако для первого предприятия существует еще более выгодная ситуация, а именно: первое предприятие сообщает заинтересованную оценку S1 = 10 по первому проекту и завышенную оценку S2 = 6 по второму. В этом

случае эффективность второго проекта Э2 13 0,3 и по-прежнему выше, чем

эффективность третьего проекта. Ставка внутреннего кредита становится равной β = Э2 – 0,2 = 0,1, и прибыль первого предприятия

П1 = 0,8 (100 – 11) + 0,8(80 66) + 12 = 94,4.

При этом первое предприятие получает финансирование в размере 70 ед. на два проекта и перераспределяет эти средства, выделяя на первый проект 20 ед., на второй – 40 ед., а 10 ед. идут на выполнение других проектов с эффективностью

= 0,2.

8.8. Механизмы совместного финансирования

Идея совместного финансирования в том, что корпоративный центр выделяет только часть ресурсов, требуемых для реализации проекта, а остальную часть выделяет само предприятие, подавшее заявку на проект.

Такие механизмы предлагались для финансирования приоритетных направлений науки и техники [41], где они были названы механизмами смешанного финансирования. Их исследования для непрерывного случая при линейных функциях затрат или функциях затрат типа Кобба-Дугласа были проведены в работе [41], где показано, что при смешанном финансировании эффективность использования централизованных сроков существенно увеличивается. Рассмотрим механизмы совместного финансирования применительно к корпорации, включающей n предприятий. Каждое предприятие может подать одну или несколько заявок на финансирование, содержащих оценку ожидаемого дохода dί и оценку требуемого финансирования Sί . Средства хί, выделяемые корпоративным центром на ί-й проект, определяются выражением

решая которое определяем новые значенияSi . Если среди них есть Si < rί, то процедуру повторяем.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Назовите основные этапы функционирования организационной системы.

2.Какой механизм управления называется механизмом открытого управления или «честной игры»?

3.Какой механизм управления называется согласованным механизмом?

4.Какой механизм называется противозатратным механизмом налогообложения (прибыли)?

5.Чему равна остаточная маргинальная рентабельность заказа?

6.Как можно вычислить эффективность простого конкурсного механизма?

7.Назовите общий вид функции производственных издержек типа КоббаДугласа.

8.В чем заключается основная идея построения оптимального механизма распределения корпоративного заказа?

9.Сформулируйте свойства механизма внутренних цен.

10.Опишите механизм внутренних цен для линейных функций производственных издержек.

11.В чем заключается механизм внутренних цен без перераспределения прибыли?

12.Какие механизмы называются согласованными механизмами распределения корпоративного заказа?

13.Сформулируйте метод решения задачи распределения корпоративного заказа для случая, когда согласованность обеспечивается путем уменьшения доли прибыли, отчисляемой Корпоративному центру.

14.Перечислите механизмы, которые характеризуются высокой оптимальностью, эффективностью, неманипулируемостью и малой вероятностью образования коалиций.

15.В чем заключается механизм внутреннего кредитования?

16.Сформулируйте правило взятия кредита.

17.Почему не работают конкурсные механизмы, если берется внешний кредит?

18.В чем заключается механизм внутреннего кредитования с гибкими ставками?

19.Какими свойствами обладает механизм внутреннего кредитования с гибкими ставками?

20.Какой механизм называется механизмом совместного финансирования?

225

ГЛАВА 9. РАЗРАБОТКА И ИССЛЕДОВАНИЕ ЭВРИСТИЧЕСКИХ МОДЕЛЕЙ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

9.1. Основные правила приоритета

Будем рассматривать задачи распределения ресурсов в следующей достаточно общей постановке. Во-первых, будем рассматривать воспроизводимые ресурсы (типа «мощности») m различных видов. Работы проекта разбиты на классы так, что каждая работа выполняется ресурсами определенного (одного) вида. Далее примем, что зависимость скорости работы от количества ресурсов является линейной вида (9.1.1). В качестве критерия оптимизации берем продолжительность проекта T. Обозначим через Nj количество ресурсов j-го вида, Pj – множество работ, выполняемых ресурсом j-го вида,суммарный объем работ j-го вида ,-

Примем продолжительности работ равными минимальным i и определим поздние сроки начала всех работ tiн и поздние сроки окончания всех работ tiо. Для этого определяем продолжительность проекта T0, не учитывая ограничений на ресурсы, и просчитываем сетевой график «с конца». Алгоритм определения поздних моментов начала и окончания работ рассмотрим на примере.

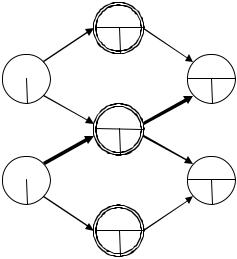
Пример 9.1.1. На рис. 9.1.1 приведен сетевой график из семи работ. В верхней половине кружка записан номер работы, в нижней слева – продолжительности i. Сначала определим ранние сроки начала и длину критического пути T0. Ранние сроки окончания указаны в квадратных скобках у соответствующих вершин. Длина критического пути равна T0 = 22. Для определения поздних сроков начала производим просчет сетевого графика с конца.

226

t4н = min(t6н,t7н)- 4 =13-7 = 6.

Продолжая таким образом, получаем:

t5н = t7н- 5 = 17-2 = 15, t3н = t6н- 3 = 13-4 = 9,

Как уже отмечалось, для решения задач распределения ресурсов применяются в общем случае эвристические алгоритмы. Рассмотрим основные эвристические правила распределения ресурсов по фронту работ.

Правило 9.1.1 (по степени критичности работ). В первую очередь начинаются работы с минимальным поздним сроком начала (поздний срок начала называется также степенью критичности работы, отсюда и название правила. Для иллюстрации этого правила рассмотрим сетевой график (рис. 9.1.1), и примем, что работы 1, 2, 6, 7 выполняются каждая единицей ресурсов первого вида, а работы 3, 4 и 5 – единицей ресурсов второго вида каждая. Примем

N1 = N2 = 1.

1шаг. t = 0. Так как t1н = 3 > t2н = 0, то выполняем работу 2.

2шаг. t = 6. Выполняем работы 1 и 5.

3шаг. t = 9. Выполнены работы 1 и 5. Начинаем работу 4, так как t4н < t3н.

4шаг. t = 15. Выполнена работа 4. Выполняем работы 3 и 7.

5шаг. t = 20. Выполнены работы 3 и 7. Выполняем работу 6.

Проект завершается за T1 = 20+9 = 29 дней.

227

Правило 9.1.2 (по минимальной продолжительности работ). В первую очередь начинается работа, имеющая минимальную продолжительность.

Пример 9.1.2. Рассмотрим сетевой график (рис. 9.1.1), и применим к нему правило 9.1.2.

1 шаг. t = 0. Начинаем работу 1, так как 1 < 2. 2 шаг. t = 3. Выполняем работы 2 и 3.

3 шаг. t = 9. Выполнены работы 2 и 3. Выполняем работу 5, так как

5 < 4.

4 шаг. t = 11. Выполняем работу 4.

5 шаг. t = 18. Выполняем по очереди работы 6 и 7 (в любом порядке). Проект завершается за T2 = 18+14 = 32 дня.

Правило 9.1.3 (по минимальному позднему сроку окончания).

Рассмотрим сетевой график (рис. 9.1.1), и применим к нему правило 9.1.3.

1шаг. t = 0. Обе работы имеют одинаковые значения t1о = t2о = 6. Поэтому начинаем любую, например, работу 1.

2шаг. t = 3. Работа 1 выполнена. Начинаем работы 2 и 3.

Проект завершается за T3 = 25+5 = 30 дней.

В данном случае наилучшее решение дает правило 9.1.1. Однако нетрудно привести примеры, когда наилучшее решение дает правило 9.1.2 или 9.1.3. Возникает задача исследования этих правил с тем, чтобы выделить случаи, в которых то или иное правило является более эффективным.

9.2. Распределение ресурсов по степени критичности работ

Определение 9.2.1. Пропускной способностью фронта работ F называется

Определение 9.2.2. Фронт работ F, такой, что C(F) < N, называется «узким местом» сетевого графика.

Заметим, что если в каком-либо интервале выполняются работы, являющиеся узким местом, то в этом интервале ресурсы используются неполностью, что может привести к увеличению продолжительности проекта. Действительно, при полной занятости ресурсов продолжительность проекта составит

Рассмотрим ряд частных случаев, когда правило 9.1.1 всегда дает оптимальное решение.

228

Пусть сетевой график имеет вид дерева (рис. 9.2.1), все работы выполняются единицей ресурсов (с фиксированной интенсивностью) и имеют одинаковые продолжительности (без ограничения общности примем = 1). В данном случае приоритетность по минимальной степени критичности эквивалентна приоритетности по максимальному рангу соответствующей вершины дерева (ранг вершины равен числу вершин пути, соединяющего данную вершину с конечной). Для случая N = 2 на рис. 9.2.1 пунктиром выделены множества работ, выполняемых одновременно, а римские цифры показывают очередность их выполнения. Минимальная продолжительность проекта равна 7.

Рис. 9.2.1

Приведем еще один частный случай, когда правило 9.1.1 дает оптимальные решения.

Будем говорить, что фронт F1 находится правее фронта F2, (F1 F2), если для любой пары (i,j) работ такой, что i F1, j F2, не существует пути, соединяющего работу i с работой j.

Рассмотрим сетевой график такой, что для любых F1 и F2, F1 F2, имеет место C(F1) ≤ C(F2). Будем называть такие сетевые графики монотонными. Содержательно это означает, что фронт работ с выполнением работ проекта не увеличивается. Если построить левосдвинутый график потребности в ресурсах (все работы начинаются в наиболее ранние моменты), то этот график будет невозрастающей функцией времени.

Гипотеза 9.2.1. Для монотонных сетевых графиков правило 9.1.1 дает оптимальное решение.

Строгого доказательства этого факта нет. Однако не удалось найти ни одного примера, опровергающего эту гипотезу. Рассмотрим сетевой график на рис. 9.2.2. Пусть N = 4.

229

Поскольку обе работы, 1 и 2, имеют одинаковые степени критичности, то распределяем ресурсы поровну. Через 6 дней начинаем работу 4, u4= 3. Оставшуюся 1 ресурса распределяем на работы 3 и 5 поровну, u3= u5= 0,5. Через 4 дня завершается работа 4 и наполовину выполнены работы 3 и 5. Далее выполняются работы 3, 5 и 7, а после завершения работ 3 и 5 выполняются работы 6, 7 и 8. Продолжительность проекта составляет T = 15 дней.

Если ресурсы могут принимать только целочисленные значения, то в интервале (6,10), когда u3= u5= 0,5, поступаем следующим образом. В интервале (6,8) выполняется работа 3, u3= 1, а в интервале (8,10) – работа 5, u5= 1. При этом выполнение работы 3 прерывается. Если прерывание работы запрещено, то правило 9.1.1 может не дать оптимального решения. В этом случае оптимальное решение выглядит следующим образом. Сначала выполняется работа 1 (или 2). Через 3 дня выполняются работы 2 и 3. Через 7 дней выполняются работы 4 и 5. И, наконец, через 11 дней выполняются работы 6, 7 и 8. Минимальная продолжительность проекта составляет T = 16 дней.

Если применение правила 9.1.1 (или любого другого правила) привело к попаданию на «узкое место», то возникает задача его устранения либо уменьшения простоев ресурсов. Рассмотрим подход к устранению «узких мест» на основе следующей задачи.

Задача редактора. Имеется n рукописей. Каждая рукопись редактируется редактором, затем направляется авторам, а потом снова возвращается редактору для окончательного редактирования. Обозначим через ai продолжительность первого редактирования i-й рукописи, bi – продолжительность работы авторов, ci – продолжительность второго редактирования. Задача заключается в определении очередности работы с рукописями редактора, минимизирующей продолжительность обработки всех рукописей.

Обозначим через i = ci-ai, qi = ai+bi. В [3] доказано, что если очередности первичной и вторичной обработок одинаковы, то оптимальная очередность