Глава 2. Статическое оценивание состояния систем газоснабжения

2.1. Формулировка задачи статического оценивания

При формулировке задачи статического оценивания будем ориентироваться на сделанный ранее выбор метода ее решения, то есть на метод взвешенных наименьших квадратов. Введем основные определения, необходимые для формирования статической математической модели решения задачи оценивания.

Обозначим вектором Z набор всех параметров, представляющих собой быстро изменяющуюся составляющую информации о гидравлической системе, и будем считать компоненты этого вектора параметрами режима [17]. Поскольку акцент исследований в работе делается на городских распределительных системах газоснабжения, то вполне допустимо считать, что течение газа в трубопроводах будет изотермическим. Тогда для установившегося потокораспределения (стационарный или статический режим) в состав вектора Z будут входить вектор расходов транспортируемой среды на участках системы Q с компонентами q_i (i=1...i_Σ, i_Σ= - полное количество участков в системе); вектор узловых потенциалов H с компонентами h_j (j=1...j_Σ, j_Σ= - полное количество узлов в системе); вектор узловых отборов G c компонентами g_j (j=1...j_Σ). Остальная исходная информация, характеризующая параметры элементов ГС (длины участков и диаметры труб на них, различного рода регуляторы и запорная арматура со своими характеристиками), меняется существенно медленнее, чем параметры режима. Совокупность этих данных будем считать априорно заданной без погрешностей и обозначать вектором D.

Связь между векторами Z и D устанавливается посредством математической модели, описывающей гидравлические процессы, протекающие в системе. Будем использовать в качестве таковой универсальную модель установившегося потокораспределения, имеющую вид [31, 32, 45]:

(2.1)

(2.2)

(2.3)

где C - матрица смежности независимых цепей (маршрутов) с размерностью ,  - число независимых цепей в расчетной схеме; K - матрица смежности контуров (циклов) с размерностью ,  - цикломатическое число графа; A - матрица инциденций с размерностью ,  - число узлов с фиксируемым узловым отбором (притоком); R - диагональная матрица с размерностью , элементы которой определяются как ;

- коэффициент гидравлического сопротивления участка i;  - коэффициент нелинейности в формулах инженерной гидравлики [57]; 0 - вектор-столбец, все компоненты которого равны нулю; - транспонированная матрица независимых цепей (маршрутов).

Символом “” в модели (2.1) - (2.3) помечены векторы, компоненты которых будем считать граничными условиями (ГУ) [45]. Применение этого термина обосновано тем обстоятельством, что выбранная конфигурация модели адаптирована к разомкнутой схеме представления объекта моделирования, обмен энергией и массой с окружающей средой для которого осуществляется через узлы. Такие узлы в дальнейшем будем считать энергоузлами (ЭУ) [31], и их общее количество равно , где и - соответственно число узлов с фиксируемым (задаваемым) потенциалом или отбором (притоком). В составе системы присутствуют так называемые энергетически нейтральные узлы, в которых g_j= 0. Будем обозначать их количество через . Тогда общее число узлов в системе определяется по соотношению . Задание ГУ обязательно для всех энергоузлов, однако при этом не важно, какая из величин фиксируется - потенциал или отбор (приток), поскольку в любом случае в модели будет фигурировать либо уравнение (2.1), либо (2.3) и она окажется замкнутой, то есть общее количество уравнений будет соответствовать числу неизвестных (компоненты вектора Q).

Подлежащие фиксации граничные условия при реализации модели в механике часто называют степенями свободы, выражая тем самым тот очевидный факт, что число компонент у вектора Z всегда больше, чем у вектора Q. Для обозначения степеней свободы в дальнейшем будем использовать вектор Y, считая его компоненты согласно [17] независимыми параметрами. Оставшиеся параметры режима будем считать зависимыми и обозначать вектором X.

Ранее говорилось, что текущее состоянии ГС в условиях изотермического течения транспортируемой среды может на практике контролироваться по результатам манометрической съемки, так что состав телеизмерений для исследуемых объектов определен технологическими причинами, и ими являются компоненты вектора H. Разумеется, что в общем случае на практике невозможно обеспечить телеизмерениями все узлы системы, поэтому будем помечать символом “э” те, которые оснащены контрольно-измерительными приборами (датчиками) и каналами связи. Совокупность телеизмерений образует вектор , который можно представить в виде суммы истинных значений параметров режима H(Y), являющихся функциями степеней свободы Y и вектора ошибок , которые возникают из-за ошибок датчиков, помех в каналах телепередачи и неодновременности снятия измерений, то есть

. (2.4)

Рассмотрим теперь вопрос о выборе совокупности независимых параметров режима, то есть компонент вектора Y. Очевидно, что здесь возможны вариации, поэтому возникает проблема рационального выбора степеней свободы, для которого известны [17] два основных требования: 1) значения выбранных параметров не должны зависеть от варианта коммутации запорно-регулирующей арматуры; 2) зависимость компонент вектора телеизмерений от них должна быть явной.

Анализ известных методов оценивания сетевых систем показал, что превалирующим считается второе условие. Его выполнение, например для ЭЭС, возможно, если вектор независимых переменных образован только комплексами напряжений узлов [17], для представления которых применяются как декартовы, так и полярные координаты. Такой вариант выбора применяется практически во всех работах, однако в ряде случаев, например при наличии сильно неравноточных измерений, необходимости учета динамики или ограничений в виде неравенств, оказывается более эффективным пойти на изменение состава вектора Y и соответствующие вычисления неявных функций и их производных. Именно в этом заключаются вычислительные проблемы традиционных методов. К сожалению, этот вопрос применительно к ГС практически не исследован, поэтому предлагается в качестве независимых параметров режима принять узловые отборы (притоки) g_j (j=1...j_e), образующие вектор G. Первое условие в этом случае выполняется автоматически в силу того, что потребление зависит в основном от хронологических факторов [22]. Что касается второго условия, то результаты проведенных исследований подтверждают возможность построения явной зависимости вектора телеизмерений от Y, без использования модели (2.1) - (2.3).

Фиксацию степеней свободы не следует путать с заданием граничных условий. Принципиальное различие вытекает из смысла решаемых задач моделирования. В первом случае решается задача оценивания (обратного анализа), где требуется определить параметры режима, наиболее близкие по значениям к вектору телеизмерений, компоненты которого определены с погрешностью. Во втором случае ставится задача прямого анализа, в которой граничные условия считаются достоверной информацией. В то же время родственность обеих задач позволяет считать анализ потокораспределения частным случаем оценивания.

Состав телеизмерений является наиболее сложным вопросом при оценивании, который решается на основе понятий нелинейной и топологической наблюдаемости объекта моделирования [18]. Пока будем полагать, что объем телеизмерений достаточен для образования базиса [17], то есть условие топологической наблюдаемости выполняется. В количественном отношении это значит, что манометрическая съемка ведется во всех энергоузлах. Разумеется, на практике такое оснащение объекта контрольно-измерительными приборами невыполнимо, однако здесь оно необходимо лишь на этапе формализации задачи. Далее будет показано, что в качестве исходной информации могут использоваться псевдоизмерения, то есть указанное ограничение может быть снято. Граничные условия для реализации модели (2.1) - (2.3) в рамках задачи оценивания являются расчетной информацией, дефицит которой исключается.

Заметим, что утечки также являются энергоузлами, хотя для них нет и не может быть никакой информации относительно местоположений и объемов без решения задачи диагностики. Ранее отмечалось, что совместное решение этой задачи с оцениванием невозможно и должна применяться их алгоритмическая структуризация. Поэтому при формулировке задачи оценивания постулируется условие, что утечки в системе отсутствуют. Таким образом, топология системы и состав ЭУ однозначно определены.

Для сделанного выбора компонент вектора состояния трубопроводной системы целевая функция в методе наименьших квадратов примет вид

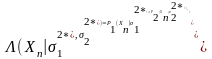(2.5)

где - дисперсия ошибки j - го телеизмерения.

Неявная зависимость h_j(G,Q), выражаемая моделью потокораспределения (2.1) - (2.3) в известных исследованиях [5, 54, 64, 140, 146] методов решения задач оценивания ГС, вынуждает прибегать к линеаризации самой модели со всеми вытекающими отсюда вычислительными проблемами.

Для преодоления этих проблем предлагается воспользоваться двумя обстоятельствами. Во-первых, в формализации задачи оценивания использовать идею функционального (энергетического) эквивалентирования абонентских подсистем (АП), суть которой изложена в [45]. Цель применения эквивалентирования заключается в том, что расчетные значения узловых потенциалов могут быть вычислены не только посредством традиционной реализации модели (2.1) - (2.3), но и через уравнение Бернулли, связывающего искомый узловой потенциал в ЭУ с барометрическим давлением:

(2.6)

В уравнении (2.6) полагается, что можно пренебречь изменением скоростного напора и различием в геодезических уровнях между узлами системы, к которым присоединяются потребители, и местами установки аппаратуры, потребляющей транспортируемую среду.

Предлагаемый способ определения расчетных значений узловых потенциалов использует хорошо известный факт, что уравнения модели потокораспределения (2.1) - (2.3), описывающие установившийся режим течения, обычно имеют малую связность, то есть каждый из измеряемых параметров зависит явно не от всех параметров режима, а только от ограниченной части из них [17]. Посредством эквивалентирования АП появляется возможность вообще исключить зависимость узлового потенциала от компонентов вектора Q.

Считая барометрическое давление величиной известной, преобразуем целевую функцию (2.5) в МНК к виду

(2.7)

Важным в (2.7) является то обстоятельство, что искомый узловой потенциал 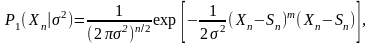для j-го ЭУ теперь зависит не опосредственно (неявно) от компонентов двух векторов G и Q , а непосредственно только от гидравлического эквивалента, присоединяемой к нему АП ( ) и потребляемого ею целевого продукта ( ). Разумеется, такая замена взаимосвязи между контролируемыми параметрами режима и степенями свободы предоставляет существенное преимущество в вычислительном плане, поскольку вместо заранее неизвестного количества параметров, влияющих на h_j, остается лишь два, причем они связаны между собой соотношением (2.6), то есть эта связь уже явная.

Второе обстоятельство, учитываемое в предлагаемой формулировке задачи оценивания, заключается в том, что при эксплуатации любых гидравлических трубопроводных систем, как правило, ведется непрерывный контроль притока транспортируемой среды через источники питания. Полагая, что исследуемая система имеет статус транспортной, то есть суммарный приток равен общему стоку, должно соблюдаться очевидное условие

(2.8)

где верхние индексы “” и “” обозначают подмножества энергоузлов присоединения источников питания и потребителей соответственно.

Есть основания считать, что учет линейного ограничения (2.8) в (2.7) является одним из средств обеспечения единственности решения. Заметим, что при традиционном варианте компонент вектора независимых переменных в (2.5) учет условия сплошности терял бы практический смысл, так как установить какую-либо взаимосвязь между расходами среды на участках не представляется возможным.

С учетом условия (2.8) целевая функция (2.7) преобразуется посредством традиционного аппарата неопределенных множителей Лагранжа к виду

(2.9)

где  - неопределенный множитель Лагранжа.

Классическая схема реализации метода наименьших квадратов сводится [48] к составлению системы нормальных уравнений, полученных в результате приравнивания нулю производных от целевой функции по искомым переменным. Искомыми на основе (2.9) параметрами будут s_j и g_j, однако в силу (2.6) только отборы среды потребителями можно считать независимыми переменными. Поэтому при нахождении условий экстремума (2.9) целевая функция оказывается сложной относительно g_j Приравнивая к нулю производные ( ) по компонентам вектора независимых переменных g_j, получим с учетом (2.6) систему нормальных уравнений

(2.10)

где - весовая функция j -го измерения.

Поскольку величины s_j по смыслу являются аналогом s_i, с той лишь разницей, что в первом случае они выражают метрические характеристики (длину и диаметр) фиктивных элементов АП, а во втором - реальных трубопроводов ГС, очевидно, что от расхода они не зависят. Тогда производные (s_j /g_j) можно считать равными нулю и пренебречь вторым членом в квадратной скобке (2.10). Независимость s_j от g_j можно обосновать из элементарных энергетических соображений. Обратим внимание на то, что по источникам питания исходными данными вместе с потенциалами являются и притоки транспортируемой среды через них в систему, в результате чего в (2.9) фигурирует соответствующее ограничение через неопределенный множитель Лагранжа. Учитывая смысл задачи оценивания, заключающийся в приближении одноименных расчетных и измеренных параметров, очевидно, что основой предлагаемого подхода является фиксация мощности потоков транспортируемой среды через источники питания. Поскольку любая модель потокораспределения строится на основе принципа минимизации диссипируемой энергии в системе, ясно, что как бы ни менялись в процессе решения задачи оценивания параметры g_j , расчетные значения узловых потенциалов , получаемые на основе модели (2.1) - (2.3), будут таковы, что s_j должны оставаться практически неизменными. Иными словами, в (2.6) s_j выступает не более как коэффициент пропорциональности между потерей напора и расходом.

Таким образом, система нормальных уравнений в методе наименьших квадратов примет вид

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

(2.11)

Систему нелинейных уравнений (2.11) можно было бы решать одним из известных способов, поскольку она является замкнутой. Количество уравнений соответствует числу энергоузлов, а для дополнительного неизвестного, которым оказывается неопределенный множитель Лагранжа, в систему достаточно включить условие (2.8). Однако уже заранее ясно, что неопределенный множитель Лагранжа не может быть константой и должен меняться в итерационном процессе. В этом случае должна быть известна его зависимость от искомых параметров, но, поскольку установить ее априорно не представляется возможным, целесообразнее исключить дополнительную переменную , сократив при этом размерность системы нормальных уравнений. В результате такого преобразования система (2.11) примет вид

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

(2.12)

Поскольку оцениваемые параметры , , для совокупности энергоузлов между собой связаны лишь уравнением (2.6), то нахождение степеней свободы посредством МНК сводится к одному из традиционных методов (в работе используется метод Ньютона).

Для удобства формирования алгоритма представим (2.12) в матричном виде:

(2.13)

(2.14)

где символ “Е” обозначает единичные матрицы. Единичная матрица в (2.13) является прямоугольной с размерами (J_H-1)×J_H и имеет блочную структуру, то есть число уравнений этого вида на единицу меньше количества энергоузлов. Единичную матрицу в (2.14) удобнее считать не матрицей столбцом, а строкой, причем число уравнений здесь всегда равно единице, вне зависимости от количества источников в системе.