
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •1.Основные определения
- •2. Линии и поверхности уровня
- •4. Предел и непрерывность функции
- •5. Частные производные функции нескольких
- •6. Геометрический смысл частных
- •10. Геометрический смысл полного
- •11. Производные сложных функций
- •12. Полный дифференциал сложной функции
- •13. Производная от функции, заданной неявно
- •14. Частные производные различных порядков
- •230100 «Информатика и вычислительная техника»
- •Часть 1
- •394026 Воронеж, Московский просп., 14
2. Линии и поверхности уровня
 В
некоторых случаях можно получить
наглядное геометрическое представление
о характере изменения функции,
рассматривая ее линии
уровня
(или поверхности
уровня
).
В
некоторых случаях можно получить
наглядное геометрическое представление
о характере изменения функции,
рассматривая ее линии
уровня
(или поверхности
уровня
).
Определение.
Линией
уровня
функции
называется множество всех точек плоскости
 ,
для которых данная функция имеет одно
и то же значение:
,
для которых данная функция имеет одно
и то же значение:

Пример.
Для функции
линиями уровня является семейство
концентрических окружностей
 с центром в точке
с центром в точке
 .
.
Определение.
Поверхностью
уровня
функции
 называется множество всех точек
пространства
,
для которых данная функция имеет одно
и то же значение.
называется множество всех точек
пространства
,
для которых данная функция имеет одно
и то же значение.
Линии и поверхности уровня постоянно встречаются в физических приложениях. Например, соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или с одинаковым средним суточным давлением, получим соответственно изотермы и изобары, знание которых важно
для прогноза погоды.
Задачи и упражнения для самостоятельной работы
Найти линии уровня в явном виде

1.1.
 1.2.
1.2.
 1.3.
1.3.

1.4.
 1.5.
1.5.
 1.6.
1.6.

1.7.

3. ЧАСТНОЕ И ПОЛНОЕ ПРИРАЩЕНИЯ ФУНКЦИИ
Пусть
-
функция двух независимых переменных
и
.
Дадим переменной
приращение
 ,
оставляя
,
оставляя
переменную неизменной. Разность

будем
называть частным
приращением функции
 по переменной
.
по переменной
.
Аналогично,
если
сохраняет постоянное значение, а
получает приращение
 ,
функция получает приращение, называемое
частным
приращением функции
по переменной
:
,
функция получает приращение, называемое
частным
приращением функции
по переменной
:
 .
.
Если обе переменные и получили соответственно приращения и , то соответствующее приращение функции:

называется полным приращением функции .
Заметим, что полное приращение функции, вообще говоря, не равно сумме частных приращений этой функции
 .
.
4. Предел и непрерывность функции
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Определение.
Окрестностью
радиуса
 точки
точки
 называется совокупность всех точек
называется совокупность всех точек
 ,
координаты которых удовлетворяют
неравенству
,
координаты которых удовлетворяют
неравенству
 ,
то есть совокупность точек, лежащих
внутри круга радиуса
,
с центром в точке
,
то есть совокупность точек, лежащих
внутри круга радиуса
,
с центром в точке

Пусть функция определенна в некоторой замкнутой области D плоскости , точка лежит в области D или на ее границе.
Определение.
Число
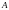 называется пределом
функции
при стремлении точки
к точке
,
если для каждого числа
называется пределом
функции
при стремлении точки
к точке
,
если для каждого числа
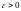 найдется такое число
найдется такое число
 ,
что для
,
что для
всех точек из окрестности радиуса точки
выполняется
неравенство

В
этом случае принято писать

Заметим, что предел функции двух переменных не должен зависеть от того, по какой линии точка стремится к точке .
Примеры.
1.
Найти предел функции
=
 в начале координат.
в начале координат.
Решение.
Поскольку, 0
 ,
а
0 при
,
а
0 при
0,
то
 = 0.
= 0.
2.
Найти предел функции
 =
=
 в начале координат.
в начале координат.
Решение. Найдем предел функции по любой прямой =
= ,
,

0.
0.
 =
=

0 при
0. Найдем теперь предел этой функции по
параболе
=
.
0 при
0. Найдем теперь предел этой функции по
параболе
=
.
 =
=
 =
=
 .
Следовательно, предела данная функция
в точке (0, 0) не имеет.
.
Следовательно, предела данная функция
в точке (0, 0) не имеет.
3.
Найти предел функции
 в начале координат.
в начале координат.
Решение. Обычного предела функция в начале координат не имеет, поскольку не определена ни в какой окрестности начала координат. Однако, на множестве Е, т.е. на плоскости без координатных осей, она имеет предел, равный нулю.
Заметим, если доопределить функцию на координатных осях нулем, то функция будет иметь и обычный предел, равный нулю.
4.Вычислить
предел

Решение. Представим
функцию
в виде
 Так как
Так как
 при
при
 ,
то
,
то

Далее,
 Поэтому искомый предел равен
Поэтому искомый предел равен

5.
Вычислить

Решение.
Перейдем к полярным координатам
 Центр полярной системы находится в
точке
Центр полярной системы находится в
точке
 ,
полярная ось параллельна оси
,
полярная ось параллельна оси
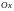 .
При стремлении
.
При стремлении
 полярный радиус
полярный радиус
 В нашем примере
В нашем примере
 ,
поэтому
,
поэтому
 Тогда
Тогда



6.
Существует ли предел
 ?
?
Решение.
Пусть точка
стремится к точке
по прямой
 ,
проходящей через точку
.
Тогда получим
,
проходящей через точку
.
Тогда получим
 Таким
образом, приближаясь к точке
по различным прямым, соответствующим
разным значениям
,
получаем разные предельные значения.
Отсюда следует, что предел данной функции
в точке
не существует.
Таким
образом, приближаясь к точке
по различным прямым, соответствующим
разным значениям
,
получаем разные предельные значения.
Отсюда следует, что предел данной функции
в точке
не существует.
7.
Вычислить предел

Решение.
Перейдем к полярной системе координат

Так
как значение предела зависит от
 ,
то при подходе к точке (0,0) по разным
направлениям получаются различные
предельные значения. Следовательно,
функция в этой точке не имеет предела.
,
то при подходе к точке (0,0) по разным
направлениям получаются различные
предельные значения. Следовательно,
функция в этой точке не имеет предела.
Определение.
Пусть точка
принадлежит области определения функции
.
Функция
называется непрерывной
в точке
,
если имеет место равенство
 причем точка
стремится к точке
произвольным образом, оставаясь в
области определения функции.
причем точка
стремится к точке
произвольным образом, оставаясь в
области определения функции.
Из определения следует, что для непрерывности функции в точке должны быть выполнены следующие условия:
функция определена в точке ;
существует предел
 ;
;предел равен значению функции в точке
 .
.
Если в некоторой точке не выполняется хотя бы одно из
условий 1)-3), то точка называется точкой разрыва функции .
Приведем еще одно определение непрерывности функции в точке, эквивалентное данному выше:
Определение. Функция называется непрерывной в точке , если :
1) функция определена в этой точке;
2) бесконечно
малым приращениям
 соответствует бесконечно малое приращение
соответствует бесконечно малое приращение

Определение. Функция, непрерывная в каждой точке
некоторой области, называется непрерывной в этой области.
Примеры.
1. Исследовать непрерывность функции . Решение. Найдем полное приращение функции
 .
Тогда
.
Тогда
 ,
то есть функция непрерывна.
,
то есть функция непрерывна.
2.
Найти точки разрыва функции
 .
.
Решение. Данная функция не определена в тех точках, где
знаменатель
дроби равен нулю:
 ,
то есть функция не определена на прямой
,
то есть функция не определена на прямой
 В остальных точках плоскости функция
определена и непрерывна. Множество
точек разрыва данной функции есть прямая
Отметим, что в любой точке
В остальных точках плоскости функция
определена и непрерывна. Множество
точек разрыва данной функции есть прямая
Отметим, что в любой точке
 , лежащей на прямой
и не совпадающей с точкой
,
существует предел функции
, лежащей на прямой
и не совпадающей с точкой
,
существует предел функции
 Поэтому точки
при
Поэтому точки
при
 можно
назвать точками устранимого разрыва:
если положить
можно
назвать точками устранимого разрыва:
если положить
 ,
то функция станет непрерывной в точке
.
В точке
имеем
,
то функция станет непрерывной в точке
.
В точке
имеем
 ,
,
то есть - точка неустранимого разрыва данной функции.
3. Исследовать на непрерывность в точке функцию

Решение. Применяя известную формулу для разности
косинусов, запишем
функцию
 в виде
в виде
 Так как
Так как
 то функция
то функция
непрерывна в точке .
Задачи и упражнения для самостоятельной работы
Вычислить пределы:
1.1.
 1.2.
1.2.
 1.3.
1.3.
 ;
;
1.4.
 1.5.
1.5.

1.6.
 1.7.
1.7.

1.8.
 1.9.
1.9.

1.10.

Докажите, что следующие пределы не существуют:
2.1
 2.2.
2.2.
 2.3.
2.3.

3.Найти точки разрыва следующих функций:
3.1.
 3.2.
3.2.

3.3.
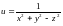 ; 3.4.
; 3.4.
 3.5.
3.5.
 ;
3.6.
;
3.6.
 3.7.
3.7.
 .
.
Ответ:
Ответ: 1.1. ;
1.2.2; 1.3.
;
1.2.2; 1.3. ;
1.4. 0; 1.5. 0; 1.6.0; 1.7.0; 1.8.1. 1.9. 0. 1.10. 2. 3.1.О(0,0);
;
1.4. 0; 1.5. 0; 1.6.0; 1.7.0; 1.8.1. 1.9. 0. 1.10. 2. 3.1.О(0,0);
3.2.
все точки окружности
 ;
;
3.3.все
точки конической поверхности
 ;
;
3.4.
все точки прямой
 ;
3.5. все точки прямых
;
3.5. все точки прямых
 ;
3.6. все точки прямых
;
3.6. все точки прямых
 ;
;
3.7.
все точки сфер
 .
.
