Оценка экстремумов риска реализации dDoS-атак на распределенные компьютерные системы
Распределенные атаки типа «отказ в обслуживании» на распределенные компьютерные системы и их компоненты обуславливают различные отказы, которые наносят ущерб и объясняют наличие соответствующих рисков. При асинхронных атаках на компоненты системы оценку общего риска РКС можно осуществить с помощью выражения
где Riski– оценка риска, осуществленная независимо для i-го компонента системы;
u – значение возможного ущерба.
Рассмотрим РКС, состоящую из 2-х компонентов. В этом случае имеем:
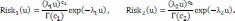
Максимумы рисков отдельных компонент РКС являются значениями функции риска от моды данного риска:
Тогда интегральный риск РКС определяется следующим образом:
Экстремумы суммарного риска в общем случае не совпадают с указанными максимумами отдельных компонент РКС. Для их определения необходимо найти производную функции суммарного риска и приравнять ее нулю. То есть:
Перенесем второе слагаемое вправо и прологарифмируем:
Раскроем скобки:
Cгруппируем слагаемые относительно u:
Введем замену переменных:
Таким образом, получаем уравнение:
График функции производной риска представлен на рис.5.1, где пересечения с осью ущербов соответствуют экстремумам функции.
Рис.5.1.Вид функции производной риска
Решением уравнения вышеприведенного уравнения является выражение:
где
поправка,
вносимая в первое решение второй
компонентой.
Поправку
определим
следующим образом:
Упростим данное уравнение подобно уравнению производной риска и, таким образом, получим:
Разделим
уравнение на
:
Уравнение подобного вида решается с помощью теоремы Виета.
Вычисляем:
Если все коэффициенты кубического уравнения вещественны, то и S вещественно, и по его знаку можно определить тип корней:
S> 0 — три вещественных корня;
S = 0 — один однократный вещественный корень и один двукратный;
S< 0 — один действительный корень и пара комплексно сопряженных.
Следовательно,
при S>
0 получаем 3 вещественных корня 
:
где
Данные
корни будут определять 3 поправки 
Минимальная и максимальная поправки определяют максимумы функции риска, что видно из рис.5.2, иллюстрирующего данный случай. Минимум же определяет поправка, которая находится между минимальной и максимальной поправками.
Рис.5.2.Интегральная оценка риска РКС, состоящей из двух компонентов и имеющей три экстремума
Возможен случай,
когда расстояние между модами рисков
двух компонент РКС невелико (рис.5.3). Для
данного случая выполняется условие S
= 0 и уравнение производной риска
будет иметь один вещественный корень,
который попадает в интервал 
.
Корень уравнения при этом равен одному из корней:
Рис.5.3. Интегральная оценка риска РКС, состоящей из двух компонентов и имеющей один экстремум
Рассмотрим случай, когда система состоит из n компонентов.
При этом первый максимум смещается вправо в результате действия поправок от других компонент.
При этом поправкиможно определить как:
При
этом на максимум влияют только min(
).
Для второго максимума первый максимум сдвигает его влево, остальные вправо.
В результате получаем, что:
Для i>2 поправки имеют следующий вид.
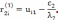
Тогда для i-го компонента получаем:
При этом для ущерба, аналогично поправкам определяем знак поправки, следующим образом:
Для случая асинхронных атак, атака на отдельный компонент РКС не влияет на работоспособность другого компонента системы, а риск распределенной системы в целом определяется как сумма рисков компонент и, следовательно, компоненты можно рассматривать как независимые.
Таким образом, ущербы, определяющие максимумы риска, выражаются следующим образом:
Введем
обозначение 
Для удобства данные поправки можно записать в виде матрицы:
Сумма элементов в i-ой строке определяет поправку для моды ущерба i-го компонента.
Таким образом, получается вектор координат ущербов, при которых функция суммарного риска имеет максимум:
Рассмотренный выше случай предполагает, что кубическое уравнение имеет три вещественных корня. Если же решение уравнения имеет один корень, то два максимума объединяется в один. Для совпадающих максимумов в i-1 и i компонентах вектор будет иметь следующий вид:
Итоговую поправку для минимума, используя данный подход определить, не представляется возможным, поэтому для их нахождения можно использовать численные методы, например метод Ньютона.