1. Длина окна и длина ряда.

• Сингулярные разложения траекторных матриц одного и того же ряда длины N, соответствующие выбору длины окна L и N–L+1 эквивалентны (с точностью до симметрии: левые сингулярные векторы ↔ правые сингулярные векторы). Следовательно, для анализа структуры временного ряда базовым методом SSA не имеет смысла брать длину окна, большую половины длины ряда.

• С учетом предыдущего замечания, чем больше длина окна, тем более детальным получается разложение исходного ряда. Таким образом, наиболее детальное разложение достигается при выборе длины окна, приблизительно равной половине длины ряда (L~N/2). Исключением являются ряды конечного ранга, для которых при любом L, большем чем ранг ряда d, и N>2d–1 число ненулевых компонент в сингулярном разложении равно d и не зависит от длины окна.

2. Длина окна и слабая разделимость.

• Так как результаты относительно слабой разделимости аддитивных составляющих временных рядов в большинстве своем асимптотические (при L,K→ ), как правило, чтобы достичь лучшей разделимости, нужно выбирать большую длину окна. Другими словами, маленькая длина окна может привести к смешиванию интерпретируемых компонент ряда.

• Если длина окна L достаточно большая (скажем, несколько дюжин), то результаты (слабой) разделимости устойчивы по отношению к небольшим изменениям L.

• С другой стороны, для решения особых задач могут быть конкретные рекомендации по выбору длины окна, соответствующие относительно небольшим N и L [60].

Самым неформализуемым шагом является шаг группировки. Для того, чтобы выделить какую-то составляющую ряда или отделить сигнал от шума, необходимо найти соответствующие искомой составляющей компоненты разложения, сгруппировать их и восстановлением получить искомый ряд.

Решению этой задачи служит визуальный способ идентификации компонент. Гибкость способа делает его привлекательным, однако эвристизм и необходимость в некоторых случаях, пакетной обработки анализируемого ряда обесценивают его простоту. Направлением развития метода, учитывающим этот недостаток, является автоматизация процедуры идентификации/группировки. Этому направлению посвящено множество работ. Суть предлагаемых методов заключается в дополнительном – периодограммном (частотном) анализе компонент разложения ряда с введением пороговых значений идентификации.

Рекомендации по решению проблемы группировки, идентификации компонент и восстановлению по ним ряда:

Изложим основные положения предлагаемых методов в соответствии с [61]:

В основание метода идентификации тренда лежит следующая идея: сингулярные вектора компонент, соответствующих тренду, ведут себя подобно самому тренду, поэтому достаточно сформулировать метод в применении к произвольному ряду.

Метод низких частот основан на частотном представлении ряда. Рассматривается разложение Фурье вещественного временного ряда

(1)

где и если – нечетное. Тогда периодограммой ряда называется функция, определенная следующим образом при

(4.2)

Значение отражает вклад в разложение ряда гармоники с частотой Считается, что ряд является трендом, если гармонические составляющие с низкими частотами дают большой вклад в его разложение Фурье. Задав параметр считается областью низких частот интервал Для ряда отношение

(4.3)

можно интерпретировать как вклад гармоник со средними и высокими частотами в разложение Фурье последовательности Считается, что ряд содержит трендовую составляющую, если для заданного порогового уровня

Метод Фурье для автоматической идентификации компонент, соответствующих экспоненциально модулированной (сокращенно – э.-м.) гармонической составляющей, тоже основан на анализе периодограмм сингулярных векторов.

Используется тот факт, что э.-м. гармонике с частотой соответствует две компоненты сингулярного разложения, сингулярные вектора которых имеют тоже э.-м. гармонический вид с теми же частотой и экспоненциальным показателем. Алгоритм метода Фурье разделяется на две части:

1. Часть 1. Используется тот факт, что периодограммы двух сингулярных векторов, соответствующих э.-м. гармонике, должны достигать максимальных значений на одной и той же частоте. Это и проверяется. Для рассматриваемой пары компонент с номерами и обозначаются и аргументы максимумов периодограмм их сингулярных векторов. Пусть – пороговое значение метода. Если где – длина сингулярного вектора, то считается, что пара соответствует э.-м. гармонике. Заметим, что является оценкой частоты найденной э.-м. гармоники. Поиск компоненты, соответствующей э.-м. гармонике с периодом 2, должен проводиться отдельно, так как ей соответствует одна компонента. В этом случае используется критерий .

2. Часть 2. В первой части метода использовалось только одно свойство периодограммы – аргумент ее максимума. Этого недостаточно, метод может ошибочно идентифицировать пары компонент, вовсе не соответствующие э.-м. гармонике. Учитывается тот факт, что два гармонических сингулярных вектора (собственных или факторных), соответствующие гармонике, не только имеют такой же период, как и сама гармоника, но также имеют разницу в фазе, примерно равную

Задается величина где и – номера двух сингулярных векторов формулой

. (4.4)

Если элементы векторов и образуют гармонические ряды с одной той же частотой 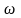и сдвигом фазы на а – целое число, то Рассматривая пары компонент, уже идентифицированные в первой части метода, и считается, что пара компонент с номерами и соответствует гармонике, только если выполняется где – заранее заданное пороговое значение. Чем больше тем строже условие. Похожим образом формулируется критерий и для гармоники с периодом 2.

Поскольку первая часть метода Фурье используется как подготовительная перед второй частью, можно зафиксировать значение установив его равным 1, что вполне достаточно для учета дискретности области определения периодограммы. Управление методом тогда будет совершаться только варьированием значения [61].

При решении последней задачи, используя хорошо проработанный аппарат SSA-прогнозирования, риск реализации ущербов рассматриваемой величины на прогнозируемом периоде можно вычислить на основе меры, предложенной в [58].