Занятие № 11
ПРОИЗВОДНАЯ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Литература: [12], с. 64-77.
Контрольные вопросы и задания
1. Дайте определение производной.
2. Каков физический смысл производной?
3. Что называется касательной к кривой?
4. В чем состоит геометрическое значение производной?
5. Докажите следующие теоремы:
– производная постоянной равна нулю;
– постоянный множитель можно выносить за знак производной;
– о производной суммы конечного числа дифференцируемых функций;
– о производной от произведения двух дифференцируемых функций;
– о производной частного от деления двух функций.
Примеры решения задач
В
примерах 1-9 найти производную
функции
.
Пример
1.
.
Решение. Для нахождения производной воспользуемся правилами дифференцирования суммы и дифференцирования степенной функции.
.
Пример
2.
.
Решение. Для нахождения производной воспользуемся правилами дифференцирования произведения, суммы и дифференцирования степенной функции.
.
Пример
3.
.
Решение. Для нахождения производной воспользуемся правилами дифференцирования частного, суммы и дифференцирования тригонометрических функций.
.
Пример
4.
.
Решение. Для нахождения производной воспользуемся правилами дифференцирования частного и дифференцирования обратных тригонометрических функций.
.
Пример
5.
.
Решение. Для нахождения производной воспользуемся правилами дифференцирования произведения, обратных тригонометрических функций, сложной функции и степенной функции.
.
Пример
6.
.
Решение. Для нахождения производной воспользуемся правилами дифференцирования показательной функции, сложной функции, частного и логарифмической функции.
.
Пример
7.
.
Решение. Прологарифмируем данную функцию и получим
.
Продифференцируем левую и правую части полученного равенства:
.
Применим к левой части правило дифференцирования сложной функции, а к правой – правила дифференцирования произведения, сложной функции, логарифмической функции и тригонометрических функций:
.
В итоге, выражая производную из этого равенства, получаем
Пример
8.
.
Решение.
В данном примере функция
задана неявно. Дифференцируем обе части
равенства по
,
рассматривая
как функцию от
,
а также применяя правила дифференцирования
показательной функции, сложной функции
и произведения:
.
Выражаем
производную
из этого равенства:
,
.
Пример
9.
.
Решение. Данная функция задана параметрически, поэтому
.
Пример
10. Найти
уравнения касательной и нормали к кривой
в точке
.
Решение. Запишем уравнения касательной и нормали:
,
.
В
данном примере координаты точки
и
.
Найдем
как производную неявной функции:
,
т.е.
,
откуда
.
Значит,
.
Отсюда получаем уравнение касательной
в точке
,
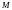
т.е.
и уравнение нормали в точке
,
т.е.
.
Задачи и упражнения для самостоятельного решения
Решить задачи: [13], 466-468, 492-497, 539-546, 547, 659-572, 593-596, 631-640, 662, 754.
Форма отчета: конспект, устный опрос, контрольная работа.