4. Механические колебания и упругие волны

4.1. Найти частоту малых колебаний системы, показанной на рисунке (ниже). Известны радиус блока , его момент инерции относительно оси вращения, масса тела и жесткость пружины . Массы нити и пружины пренебрежимо малы, нить по блоку не скользит, трения в оси блока нет.

Решение. Уравнения движения тела m и блока(Рис.1): (1), (2).

Здесь cилы натяжения нитей по обеим сторонам блока, причем , где х-деформация пружины. Кинематические соотношения: (3). Подставляя (3) в (2) и исключая с помощью (1), получим: 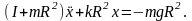Отсюда частота колебаний системы

4 .2. Однородный стержень массы = 1,5 кг, висящий на двух одинаковых нитях длины = 90 см (см. рис. ниже), повернули на малый угол вокруг вертикальной оси, проходящей через его середину C. При этом нити отклонились на угол = 5,0°. Затем стержень отпустили, и он начал совершать малые колебания. Найти:

а) период колебаний;

б) энергию колебаний стержня.

Решение. Период и полную энергию крутильных колебаний системы, показанной на рисунке, определим на основе энергетических соображений.

Согласно начальным данным, уравнение крутильных колебаний системы имеет вид , где - частота колебаний, - максимальный угол поворота стержня относительно оси ОО.

Между углом отклонения нитей от вертикальных положений и угол поворота стержня имеется определенная связь, которую приближенно можно определить равенством , где - длинна стержня. Получая , что является максимальным значением угла отклонения нити, угловая амплитуда колебаний стержня и, следовательно, уравнение колебаний будет иметь вид . При этом угловая скорость поворота стержня относительно оси ОО

.

Максимальная угловая скорость стержня при прохождении им положения равновесия (низкого уровня) равна . При отклонении нитей на угол потенциальная энергия стержня увеличивается на

.

При малых колебаниях .

В последующем, когда стержень будет проходить нижнее положение, потенциальная энергия полностью перейдет в кинетическую энергию . Итак имеем равенство Отсюда получаем частоту и период колебаний:

, .

При этом полная механическая энергия колеблющегося стержня .

4.3. Два шара с массами = 1,0 кг и = 2,0 кг насажены на тонкий гладкий горизонтальный стержень (рис.). Шары связаны между собой легкой пружинкой с жесткостью = 24 Н/м, Левому шару сообщили начальную скорость = 12 см/с. Найти:

а ) частоту колебаний системы в процессе движения;

б) энергию и амплитуду колебаний.

Решение. Шары будут совершать колебания относительно их центра масс (между прочим, подвижного) с частотой , где . Для =1,0 кг, =2,0 кг, к=24 Н/М =6 1/c. Энергия колебаний равна собственной энергии колеблющихся шаров в Ц-системе, т.е. мДж. Амплитуду колебаний найдем из условия :

см.

4.4. Однородный стержень длины совершает малые колебания вокруг горизонтальной оси , перпендикулярной к стержню и проходящей через одну из его точек. Найти расстояние между центром инерции стержня и осью ’, при котором период колебаний будет наименьшим.

Решение. Обозначим расстояние между центром стержня (центром масс) и осью ОО’ через x. Если период маятника при некотором значении х наименьший, то соответствующая частота колебаний максимальна. Для физического маятника . Здесь . Тогда . В точке экстремального значения (или ) производная . Отсюда имеем Как видно, знак первой производной от по х при переходе через точку изменяется с плюса на минус. Следовательно, .

4.5. Частицу сместили из положения равновесия на расстояние = 1,0 см и предоставили самой себе. Какой путь пройдет, колеблясь, эта частица до полной остановки, если логарифмический декремент затухания = 0,020?

Решение. Согласно данным задачи частица совершает колебания по закону , где . При известном декременте затухания требуется найти путь, пройденный частицей до полной ее остановки.

Представим амплитуду колебаний в виде и образуем последовательность ее значений через каждый полупериод колебаний частицы:

(1)

Нечетные члены последовательности соответствуют положительным смещениям частицы, четные — отрицательным. Поэтому путь, проходимый частицей за п-й полупериод будет равен:

(2)

Последовательность представляет собой бесконечную убывающую геометрическую прогрессию, первый член которой , а знаменатель . Полный путь частицы равен сумме членов этой прогрессии: . По условию задачи .