1.9.6.3. Принцип двойственности

Обращение частичного порядка является частичным порядком: двойственным к первому.

Поэтому в любой общей теореме о частично упорядоченных множествах можно всюду заменить отношение  отношением , не нарушив её истинности.

Лемма: В любом частично упорядоченном множестве может существовать не более одного наименьшего и не более одного наибольшего элемента.

Доказательство: Пусть О и O* – два наименьших элемента . Тогда (так как О– наименьший элемент) и (так как О*– наименьший элемент).

Согласно свойству 2 (стр. 45) отсюда следует: .

Замечание: Существует частично упорядоченные множества без универсальных границ. Таково множество вещественных чисел с обычным отношением порядка (если оно не расширено формальным присвоением ).

Примеры.

Задачник §2 № 1 – 6; 12 – 14.

1.9.7. Представление отношений в эвм

Пусть и |A| = n. Перенумеруем элементы множества А. Тогда отношение R можно представить матрицей R из нулей и единиц, где

(i = 1, …, n; j = 1, …, n).

Матрица отношения R обозначается .

1.10. Соответствия. Функции. Операции. Отображения

Соответствие – способ задания взаимосвязей между элементами множества (например, с отношениями). Частными случаями соответствий являются функции, преобразования, операции и т. д.

1.10.1. Соответствия и их свойства

Рассмотрим два множества А и В. Если для каждого элемента аА указан элемент bB, то говорят, что между множествами А и В установлено соответствие. Обозначим его G. Тогда G состоит из множества упорядоченных пар (a, b) таких, что аА и bB, т. е. соответствием между множествами А и В называется подмножество G прямого произведения этих множеств . При этом не обязательно, чтобы в соответствии участвовали все элементы множеств А и В.

Образом элемента а при соответствии G называется множество такое, что {b| {b|(a, b)G}.

П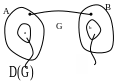 рообразом элемента b при соответствии G называется множество Coim(b) = {a| (a, b)G}.

Областью значений соответствия G называется множество

Областью определения соответствия G называется множество

Рис.7.

. .

Иначе

Область определения соответствия G – множество {a: (a, b)G}.

Область значений соответствия G – множество

{b: (a, b)G}. (рис. 7)

Свойства соответствий GAB:

1. Всюду (полностью) определённое соответствие –если

Частично определённое соответствие – в противном случае.

2. Сюръективное соответствие – если . (Рис. 7).

Образом элемента а в множестве В при соответствии G называется множество всех bB, соответствующих элементу аА.

Прообразом элемента b в множестве А при соответствии G, называется множество всех аА, которым соответствует bB.

Для каждого соответствия G существует обратное соответствие G^-1, которое любому bB сопоставляет аА, причём

G^-1={(b, a)| (a, b)G}.

3. Функциональное (однозначное) соответствие – если образом элемента а из области определения является единственный элемент b из области значений .

4. Взаимно однозначное соответствие – если оно:

а) всюду определено; б) сюръективно; в) функционально; прообразом любого элемента b из области значений является единственный элемент а из области определения .

Если между множеством А и В существует взаимно однозначное соответствие, то мощности этих множеств равны, т. е. |A|=|B|. В таком случае говорят, что множества А и В равномощны. Этот факт позволяет:

• установить равенство мощностей двух множеств, не вычисляя этих множеств;

• вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется.

Множества, равномощные множеству натуральных чисел N, называются счётными.

Множества, равномощные множеству вещественных чисел R, называются континуальными.

П ример 1. Пусть G – множество всех пар действительных чисел

(х, у), удовлетворяющих соотношению Графически такое соответствие представляет собой круг радиуса R=1 с центром в точке (3, 2). Таким образом, круг G задаёт соответствие между R и R (осью абсцисс и осью ординат). Найти:

а) образы и прообразы чисел 2, 3, 4;

б) образы и прообразы отрезков [2, 3], [2, 4].

Каковы свойства соответствия G?

а) Образом числа (на оси абсцисс) при соответствии G (cм. рис) является единственное число (на оси ординат). Образ числа 3 при соответствии G есть множество всех действительных чисел отрезка [1, 3], а образ числа 4 – число 2.

Прообразом числа (на оси ординат) является числа отрезка [2, 4] (на оси абсцисс), прообразом числа 3 при соответствии G – число 3, а прообраза числа 4 при соответствии G не существует.

б) Образом множества чисел отрезка является объединение образов всех чисел отрезка, т. е. отрезок . Аналогично образом отрезка [2, 4] будет отрезок [1, 3] при соответствии G.

Прообраз отрезка [2, 3] при соответствии G – это отрезок [2, 4], а прообраз отрезка [2, 4] – также [2, 4].

Так как соответствие G установлено на множестве действительных чисел: , то оно является:

• частично определённым, так как , ( );

• не сюръективным, поскольку , ( );

• не функциональным, ибо для любого числа отрезка

[2, 4] = (кроме чисел 2 и 4) отсутствует единственность образа;

• не взаимно однозначным, т. к. отсутствуют необходимые условия: G не является всюду определённым на R, не сюръективно, не функционально, а также для любого числа отрезка [1, 3] = (кроме чисел 1 и 3) отсутствует единственность прообраза.

Если определить соответствие , то, очевидно, оно будет всюду определённым и сюръективным, однако останется не функциональным и не взаимнооднозначным.

П ример 2. Пусть G – множество точек прямой линии, удовлетворяющих соотношению х – 2 = у при х, у  0. Каковы свойства соответствия?

1. Если соответствие G задано на множестве действительных чисел: G=RR , то G:

• частично определено, так как

• не сюръективно, так как , ( )- множество всех положительных действительных чисел с нулём;

• функционально, т. к. лю

• бому х из области определения соответствует единственный у из области значений;

• не взаимно однозначно, так как не выполняются условия – всюду определённости и сюръективности.

В случае, если G задано на множестве с нулём, т. е. , тогда соответствие G:

• частично определено, так как и ;

• сюръективно, поскольку ;

• функционально;

• не взаимно однозначно, так как не выполняется условие – всюду определённости.

3. При соответствие G:

• всюду определено;

• сюръективно;

• функционально;

• взаимно однозначно, так как наряду с выполнением указанных условий имеет место также единственность прообраза для любого .

Пример3. англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Каковы свойства этого соответствия?

Данное соответствие не является:

• всюду определённым (всегда можно найти английское слово не содержащееся в словаре);

• сюръективным (по отношению русских слов, имеющихся в словаре);

• функциональным (одному английскому слову ставится в соответствие, как правило, несколько русских);

• взаимно однозначным (в силу предыдущего).

Пример 4. Пусть множества β(U), где U = {a, b, c} и B₃ определены следующим образом:

β(U) – множество всех подмножеств (булеан) множества U = {a, b, c};

B₃– множество всех двоичных векторов длины 3,

т. е. , где А={0, 1}.

Показать, что между множествами β(U) и B₃ имеет место взаимно однозначное соответствие.

β(U) = {, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}};

|β(U)| = 8,

B₃= {(0, 0, 0}, (0, 0, 1), (0, 1, 0); (0, 1, 1); (1, 0, 1), (1, 1, 0), (1, 1, 1)};

| B₃| = 8.

Установим следующее соответствие G между множествами из β(U) и векторами из B_3:

• если в множестве β(U) присутствует элемент а, то в соответствующем ему векторе из B₃ первая компонента равна 1, а если отсутствует – то 0;

• аналогичное соответствие установим между элементом с в множестве из β(U) и значением третьей компоненты вектора из B₃.

Например, множеству {b} из β(U) соответствует вектор

(0, 1, 0) из B₃, множеству {a, c} – вектор (1, 0, 1) и т. д.:

G:   (0,0, 0), {a}  (1, 0, 0), {b}  (0, 1, 0),

{c}  (0, 0, 1), {a, b}  (1, 1, 0), {a, c}  (1, 0, 1),

{b, c}  (0, 1, 1), {a, b, c}  (1, 1, 1).

Очевидно, что установленное таким образом соответствие G является взаимно однозначным, так как выполняются все условия для взаимнооднозначного соответствия.

Пример 5. Каковы свойства соответствия между множеством N натуральных чисел и множеством M₂ⁿ степеней двойки:

?

• Соответствие G взаимно однозначно:

• всюду определено, так как ;-

• сюръективно, т. к. ;

• функционально, т. к. любому nN соответствует единственный образ ;

• имеет единственность прообраза, так как для любого существует единственное nN.

Пример 6. Используя определение равномощности множеств, показать, что множество натуральных чисел, являющихся степенями двойки, счётно.

• Для доказательства следует установить взаимно однозначное соответствие между множествами и N.

Если каждому натуральному nN поставить в соответствие число , то установленное таким образом соответствие , очевидно является взаимно однозначным (удовлетворяет всем требованиям для взаимно однозначного соответствия, (см. пример 5) и представляет множество всех векторов G.

А так как мощность множества N счётна, то из установленной взаимной однозначности между множествами N и , согласно определению равномощности бесконечных множеств, следует, что множество также счётно.

Упражнения стр. 83.